題目鏈接
https://leetcode.cn/problems/longest-palindromic-subsequence/description/?utm_source=LCUS&utm_medium=ip_redirect&utm_campaign=transfer2china
目錄
題目描述：
暴力遞歸：
動態規劃：
題目描述：
給你一個字符串?s?，找出其中最長的回文子序列，并返回該序列的長度。子序列定義為：不改變剩余字符順序的情況下，刪除某些字符或者不刪除任何字符形成的一個序列。
示例 1：
輸入：s = "bbbab" 輸出：4 解釋：一個可能的最長回文子序列為 "bbbb" 。示例 2：
輸入：s = "cbbd" 輸出：2 解釋：一個可能的最長回文子序列為 "bb" 。提示：
1 <= s.length <= 1000s?僅由小寫英文字母組成
這道題的知識點是動態規劃，可是如果直接從動態規劃講可能有點不容易理解。
所以本篇文章就是從暴力遞歸到動態規劃。
從題目中我們可以得出：本題找的是可以不連續的回文子串然后返回其最大序列的長度。
也就是說：
a2b42a
的最長回文子序列為：a2b2a或a242a 這兩個都可以因為它們返回的都是5
暴力遞歸：
我們先寫一個可以返回最長的回文子序列長度的函數：
//主函數
public int longestPalindromeSubseq(String s) {char[] str = s.toCharArray();return maxString(str, 0, str.length-1);
}//假設該函數可以返回最長回文子序列的長度
public static int maxString(char[] str, int l, int r) {}我們寫的 maxString() 方法可以返回 str 字符串[l, r]區間的最長回文子序列的長度?。
通過分析可以得出以下結論：
兩種特殊情況：
- 首先我們可以得到當 l 和 r 相等就證明此時只有一個字符那么它的返回值就是 1 。
- 如果傳入的數組只有兩個字符即 l + 1 == r?那么此時如果這兩個字符相等就返回 2 ，如果不相等就返回 1 。
普遍情況：
- 兩邊的字符都不存在于最長的回文子序列中。例：a1221b? ? ->? ?1221;
- 右邊的字符不存在在于最長的回文子序列中。例：1221b? ? ->? ?1221;
- 左邊的字符不存在在于最長的回文子序列中。例：a1221? ? ->? ?1221;
- 兩邊的字符都存在于最長的回文子序列中。例：1w221? ? ->? ?1221。
?此時代碼就可以這樣寫：
//主函數
public int longestPalindromeSubseq(String s) {char[] str = s.toCharArray();return maxString(str, 0, str.length-1);
}//假設該函數可以返回最長回文子序列的長度
public static int maxString(char[] str, int l, int r) {//先判斷兩種特殊情況if (l == r){return 1;}if (l + 1 == r){return str[l] == str[r] ? 2 : 1;}//余下的四種情況int a1 = maxString(str, l + 1, r - 1);int a2 = maxString(str, l, r - 1);int a3 = maxString(str, l + 1, r);int a4 = str[l] == str[r] ? 2 + maxString(str, l + 1, r - 1) : 0;//因為題目要求返回最長序列長度 所以需要返回這四個的最大值return Math.max(Math.max(a1, a2), Math.max(a3, a4));
}?此時我們可以提交以下：
?雖然沒通過但是從它的報錯信息可以看出，我們的思路是沒問題的。
動態規劃：
我們有了遞歸版本后就可以根據它來寫出動態規劃版本了。
?因為在maxString() 方法中只有 l 和 r 是變量，而它們兩個的取值范圍都是 [0，str.length - 1]?
此時我們就可以通過創建一個二維數組將?l 和 r 所有情況都列舉出來然后返回數組[0，str.length - 1] 下標的值就可以得出答案了。
我們先假設長度只有 5 ，那么我們就可以創建如下的二維數組 l 行，r 列
public static int maxString(char[] str, int l, int r) {int[][] arr = new int[str.length][str.length];}?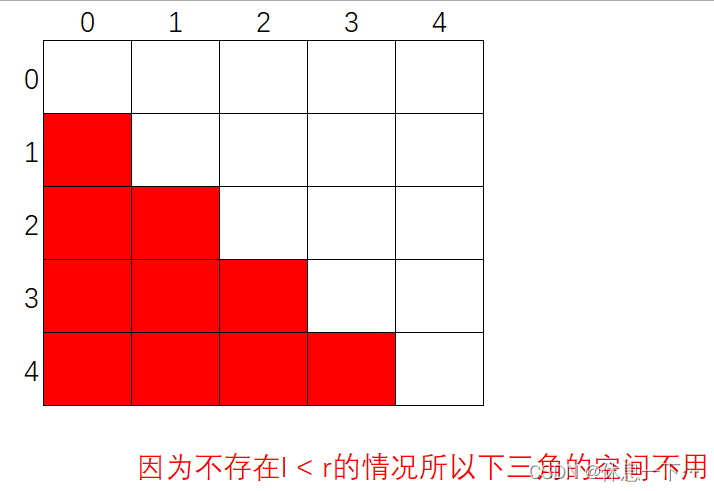
接下來的填表階段就可以根據遞歸函數直接填（以“a1221”為例子）：?
?
?
此時 [0， 4] 位置的值就是最終答案。?
?根據每個位置的關系就將遞歸優化成：
public static int maxString(char[] str, int l, int r) {int[][] arr = new int[str.length][str.length];//因為不存在l < r的情況所以下三角的空間不用for (int i = 0; i < str.length; i++) {if (i == 0){//填第一條對角線int j = 0;while(j < str.length) {arr[j][j] = 1;j++;}}else if (i == 1) {//填第二條斜線int j = 1;while(j < str.length) {arr[j - 1][j] = (str[j - 1] == str[j]) ? 2 : 1;j++;}}else {//其他int j = i;int k = 0;while(j < str.length){int a1 = arr[k + 1][j - 1];int a2 = arr[k][j - 1];int a3 = arr[k + 1][j];int a4 = str[k] == str[j] ? 2 + arr[k + 1][j - 1] : 0;arr[k][j] = Math.max(Math.max(a1, a2), Math.max(a3, a4));j++;k++;}}}return arr[0][str.length-1];
}此時再提交就過了。?
?
)
