題目：

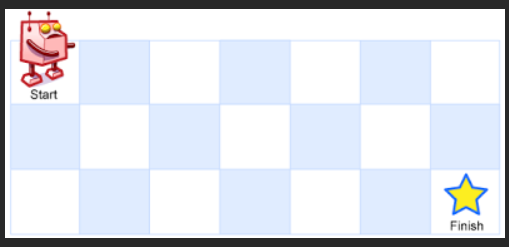
一個機器人位于一個?m x n?網格的左上角 （起始點在下圖中標記為 “Start” ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為 “Finish” ）。

問總共有多少條不同的路徑？

來源：力扣（LeetCode）
鏈接：力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

示例：

示例 1：

?

輸入：m = 3, n = 7
輸出：28

示例 2：

輸入：m = 3, n = 2
輸出：3

解釋：

從左上角開始，總共有 3 條路徑可以到達右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

輸入：m = 7, n = 3
輸出：28

示例4：

輸入：m = 3, n = 3

輸出：6

解法：

由于起點在右上角，終點在右下角，所以必然需要向右走n-1次，向下走m-1次，只是向右向下的順序不同，所以轉為組合問題。一共需要走n-1+m-1次，其中有n-1次是向右走，剩下都是向下走，所以C（n-1+m-1，n-1）。

知識點：

1.math.factorial(n)：n是正整數，返回給定數字n的階乘。

代碼：

class Solution:def uniquePaths(self, m: int, n: int) -> int:def CombinationNumber(n, m):if m <= n:return factorial(n) / (factorial(n - m) * factorial(m))return int(CombinationNumber(m - 1 + n - 1, m - 1))