面對需求的不確定性,報童模型是做庫存優化的常見模型。而標準報童模型假設價格是固定的,此時求解一個線性規劃問題,可以得到最優訂貨量,這種模型存在局限性。因為現實世界中價格與需求存在一定的關系,本文假設需求q是價格p的線性函數,基于歷史需求數據學習回歸直線的參數并計算擬合殘差,帶入到報童模型中,此時的報童模型變成一個二次規劃問題,其目標函數是關于價格p是二次的。
方法
為提高報童模型的準確性,使用SAA算法解決隨機優化問題,并與其他方法做對比。
對標準報童模型做的三個擴展
擴展1:允許rush order
當售賣當天需求量過高時,允許報童緊急訂報,只是價格g比一般訂購價格c稍高,即g>c;
如果定貨太多,那么每份報紙會產生持貨成本t,特別地,如果允許以一定價格回退給廠商,那么t<0 。但在這個文章中,僅考慮t>0的情況。
符號說明:
單份報紙的售價為p;
訂貨量是q;
目標函數是
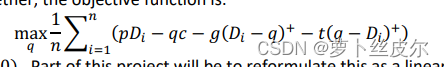
擴展2:需求與價格呈線性相關
假設需求與價格的線性回歸模型如下
D = β 0 + β 1 p + ? i D=\beta_0+\beta_1p+\epsilon_i D=β0?+β1?p+?i?
根據給定的數據集(含價格和需求量,即 { ( p i , D i ) ∣ i = 1 , 2 , . . . , n } \{(p_i,D_i)|i=1,2,...,n\} {(pi?,Di?)∣i=1,2,...,n}),找出最佳擬合線性回歸函數的參數。假設干擾項 ? i \epsilon_i ?i?具有隨機性,根據歷史數據 { ( p i , D i ) ∣ i = 1 , 2 , . . . , n } \{(p_i,D_i)|i=1,2,...,n\} {(pi?,Di?)∣i=1,2,...,n}學習到參數 β 0 , β 1 \beta_0,\beta_1 β0?,β1?,計算殘差值 { ? i ∣ i = 1 , 2 , . . . , n } \{\epsilon_i|i=1,2,...,n\} {?i?∣i=1,2,...,n}。
- 對于價格固定的標準報童模型,求最優訂貨量
如果新價格p出現,將計算好的殘差值 { ? i ∣ i = 1 , 2 , . . . , n } \{\epsilon_i|i=1,2,...,n\} {?i?∣i=1,2,...,n}和新價格p帶入模型 D = β 0 + β 1 p + ? i D=\beta_0+\beta_1p+\epsilon_i D=β0?+β1?p+?i?,可以得到新價格p所對應的需求量估計值 { D i ^ ∣ i = 1 , 2 , . . . , n } \{\hat{D_i}|i=1,2,...,n\} {Di?^?∣i=1,2,...,n},這些估計值會帶入到標準報童模型中,求解該線性規劃問題,從而得到最優訂貨量。
關于計算需求量估計值的進一步解釋,比如:估計參數 β 0 = 1000 , β 1 = ? 2 \beta_0=1000,\beta_1=-2 β0?=1000,β1?=?2,現有兩個樣本的擬合殘差是15和-9,對于新價格2來說,需求量估計值有
1000 ? 2 ? 2 + 15 = 1011 1000-2*2+15=1011 1000?2?2+15=1011,
1000 ? 2 ? 2 ? 9 = 987 1000-2*2-9=987 1000?2?2?9=987 - 對于價格不固定的擴展報童模型,求最優訂貨量和最優價格
此時,目標函數
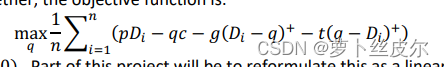
中 p ? D i p*D_i p?Di?就會變成 p ? ( β 0 + β 1 p + ? i ) p*(\beta_0+\beta_1p+\epsilon_i) p?(β0?+β1?p+?i?),這是價格p的二次函數。
注意:上面目標函數中的 D i D_i Di?指的是新價格p所對應的第i個需求估計值,而不是原數據集中第i個樣本的需求值。
我覺得沒有疑問了,這本身就是一個關于價格p的二次優化問題。
注:
為了求解這個問題,引入啞變量 h i h_i hi?,表示第i天成本的負值。如此一來,目標函數——利潤函數可以表示為收益+成本負值的平均,其中收益指 p ? D i p*D_i p?Di?,成本負值指 h i h_i hi?。


擴展3:分析數據集對最優訂貨量和最優價格的影響(最優訂購量、最優價格的敏感性分析)
對原數據集做重采樣,計算最優訂貨量、最優價格、對應的期望利潤值。
任務
- 根據給定數據集,估計出需求與價格之間的線性回歸方程;
- 給定參數c=0.5,g=0.75,t=0.15,利用殘差數據 { ? i ∣ i = 1 , 2 , . . . , n } \{\epsilon_i|i=1,2,...,n\} {?i?∣i=1,2,...,n},求價格p=1時的需求量估計值 { D i ^ ∣ i = 1 , 2 , . . . , n } \{\hat{D_i}|i=1,2,...,n\} {Di?^?∣i=1,2,...,n};
- 求價格p=1時的最優訂貨量(這是一個線性規劃問題);
- 假設價格不是固定的,將需求量與價格的線性回歸方程帶入到報童模型中,解QP(二次規劃問題,目標函數含價格的平方項),得最優訂貨量、最優價格;
- 分析最優價格、最優訂貨量是否對數據集敏感。對原數據集做重采樣,重新估計需求與價格之間的線性回歸函數參數 ,求最優價格和最優訂貨量;
- 重復上述重采樣、擬合操作,得到多組最優訂貨量和最優價格;為得到的最優訂貨量、最優價格、期望利潤繪制直方圖,觀察統計規律。
建模
價格固定時
下面是思路,我用黃色熒光筆標了步驟,即
如果新價格p出現,將計算好的殘差值 { ? i ∣ i = 1 , 2 , . . . , n } \{\epsilon_i|i=1,2,...,n\} {?i?∣i=1,2,...,n}和新價格p帶入模型 D = β 0 + β 1 p + ? i D=\beta_0+\beta_1p+\epsilon_i D=β0?+β1?p+?i?,可以得到新價格p所對應的需求量估計值 { D i ^ ∣ i = 1 , 2 , . . . , n } \{\hat{D_i}|i=1,2,...,n\} {Di?^?∣i=1,2,...,n},這些估計值會帶入到標準報童模型中,求解該線性規劃問題,從而得到最優訂貨量。
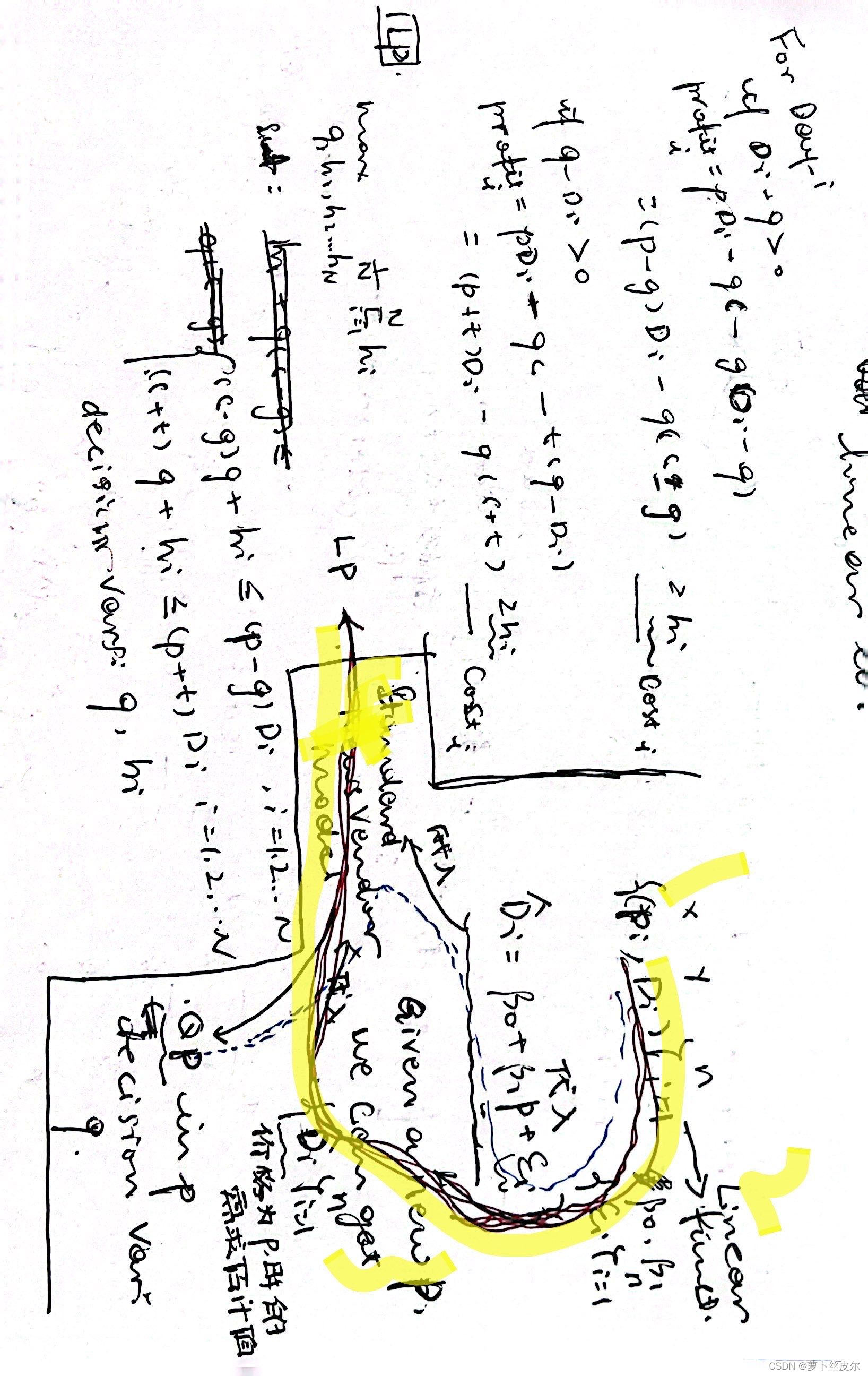

上述模型的含義:目標函數是最大化利潤,引入啞變量 h i h_i hi?表示第’i天的成本負值。
上面畫黃線的約束表示:不管需求量大于還是小于訂貨量,利潤都大于 h i h_i hi?。換言之,限制利潤(不管需求量大于還是小于訂貨量)大于等于一個變量,這個變量大于等于負無窮。
??為什么成本負值數組h的約束不是 0 > h > ? inf ? 0>h>-\inf 0>h>?inf 做實驗的時候,加上試試。會影響結果
將上述約束化簡成Gurobi建模所需要的形式(如下圖的藍筆)
注:“Gurobi建模所需要的形式”是指“明確哪些是決策變量,哪些是決策變量的系數,哪些是右端項”,這里的決策變量有 q , h 1 , . . . h N q,h_1,...h_N q,h1?,...hN?。
化簡步驟見圖中黑筆
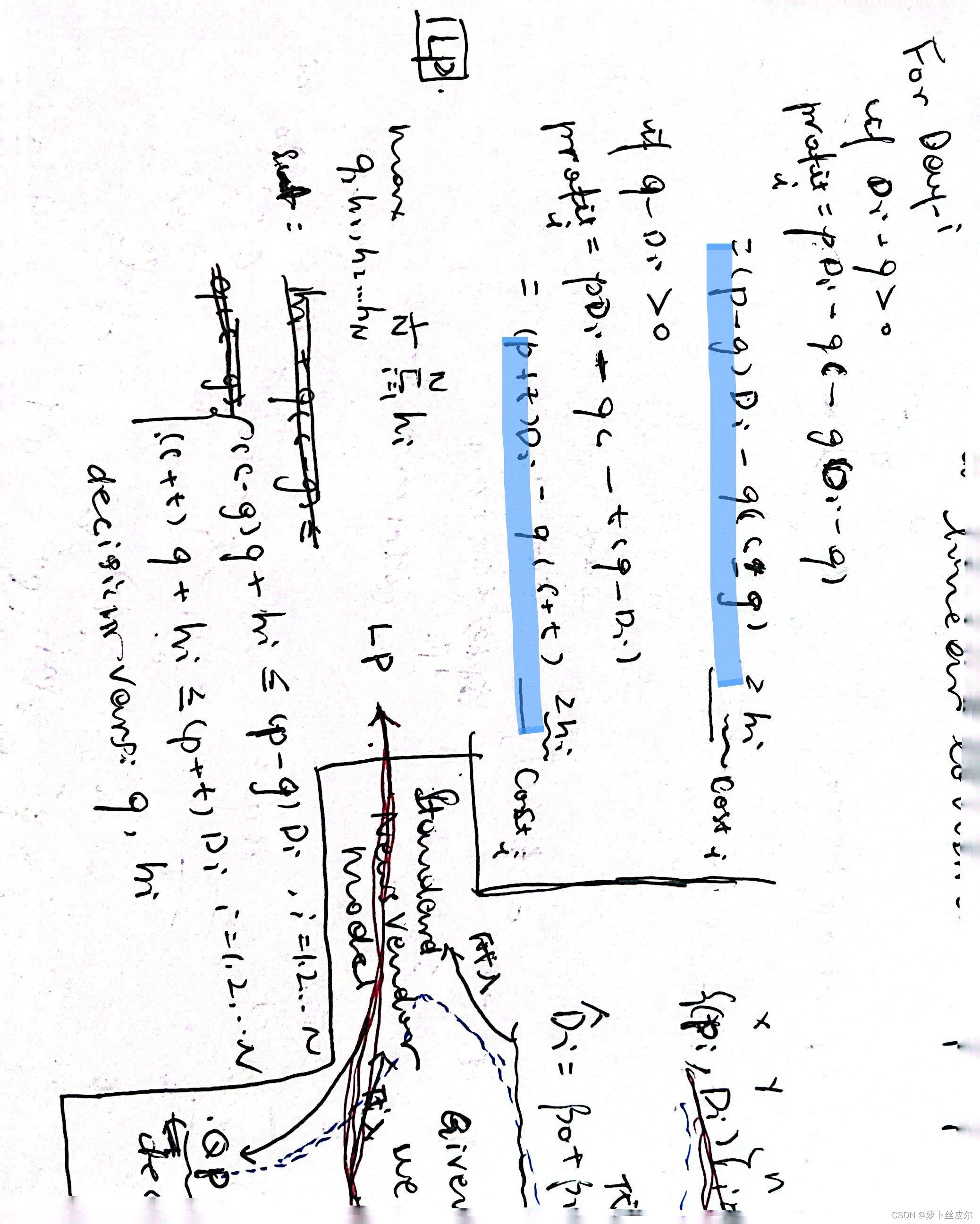
價格不固定時
我用藍筆標注了步驟:
首先,獲取需求-價格數據集,估計線性回歸參數并計算殘差數據;
接著,把 D = β 0 + β 1 p + ? i D=\beta_0+\beta_1p+\epsilon_i D=β0?+β1?p+?i?帶入到標準報童模型中,會得到一個二次規劃問題。
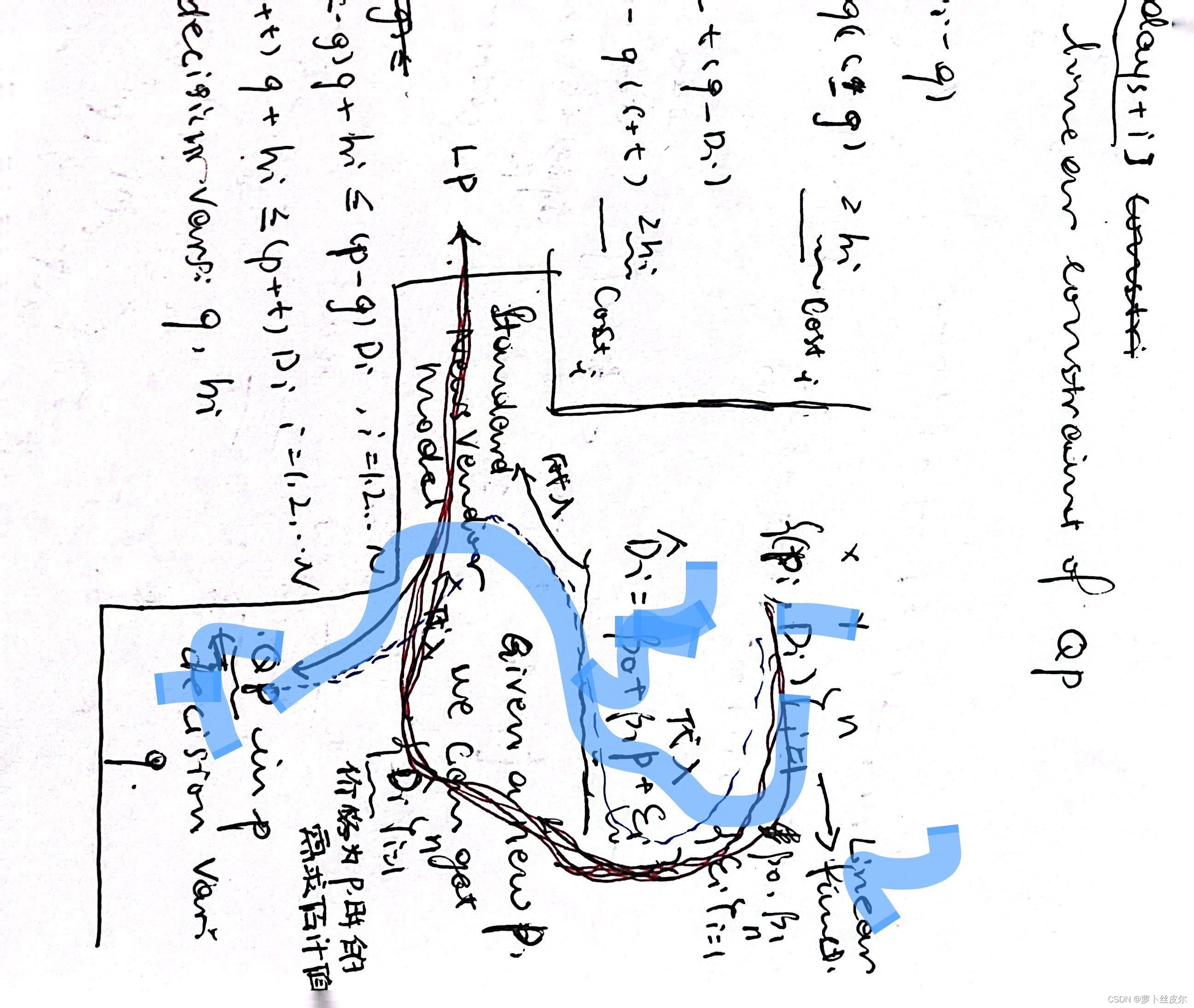
將之前的擬合結果——殘差數據、擬合函數參數等,帶入到上述模型中,得到需求量估計值 D i D_i Di?,得到如下模型:
記錄一個我沒看懂的地方。我覺得作者的轉換并沒有把二次約束轉成線性約束啊,難道是我對“二次規劃”的定義理解出錯了?我以為的二次規劃是,目標函數是二次的,約束是一次的 數學優化問題。

關于上圖的問題,我在紙上列了一下,作者的Gurobi模型應該是把上面兩個約束的二次項 p 2 p^2 p2拿掉了(用報告里面的話說:拿到目標函數中了)。
??為什么可以直接拿掉呢
關于上面的約束如何化簡成jupyter文件中Gurobi模型,我在草稿紙上簡單列了一下,藍色熒光筆標注的是Gurobi建模時所用的約束。
約束1:

約束2:

上圖還有一個問題是,目標函數中決策變量 h i h_i hi?的系數應該是1。這一點可以從兩個地方看出來:第一,老師給的作業說明(見上面“擴展2”中, h i h_i hi?的含義說明——成本負值);第二,作者的Gurobi建模obj數組中目標函數系數的指定。
最優解的穩定性分析
目標:探究使用不同的數據集是否會影響到最優解——最優價格和最優訂貨量
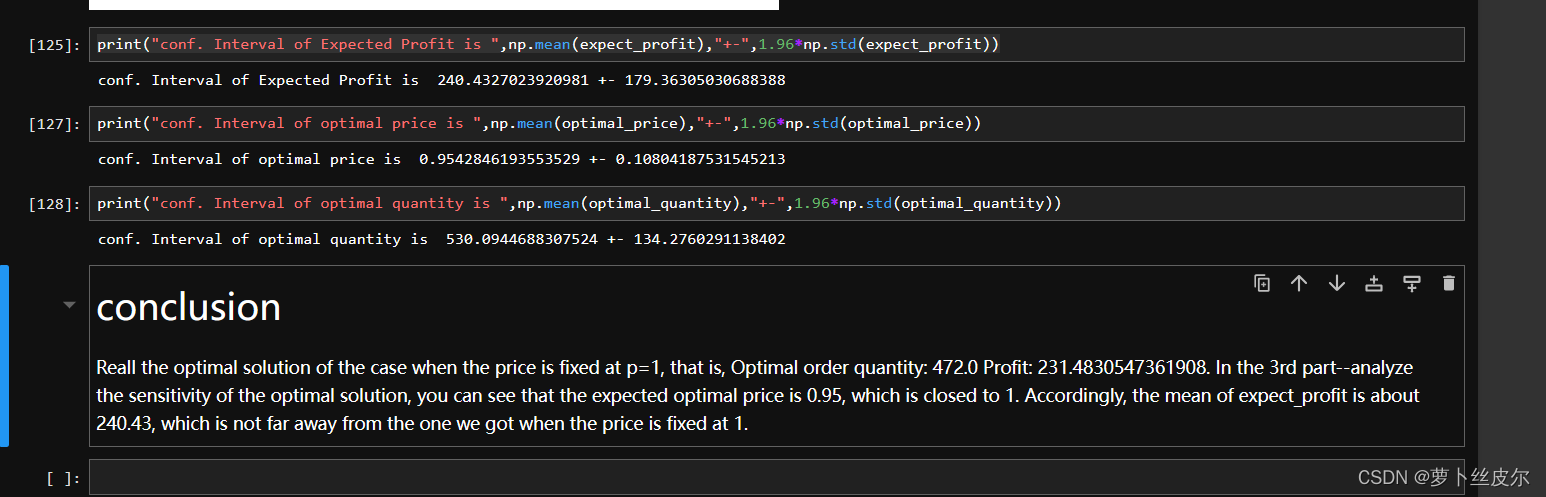
做法:對原數據集做1000次重采樣,每次采樣隨機抽取99組樣本形成新數據集。然后,針對新數據集,計算并收集最優訂貨量和最優價格,以及對應的最優利潤expect_profit。繪制最優訂貨量、最優價格、最優價格的分布直方圖,發現大致服從正態分布,且最優價格與之前LP中的預定價格1相差不大,expect_profit的均值也與之前LP的expect_profit相差不大。
注:新數據集與原數據集樣本順序是不同的。(我覺得這里有些不妥……應該設計新數據集是原數據集的子集,然后觀察最優解的統計規律)
我給這個報告添加了一個conclusion,如下圖