數據結構【第4章】——棧與隊列

隊列是只允許在一端進行插入操作、而在另-端進行刪除操作的線性表。

棧

棧與隊列：棧是限定僅在表尾進行插入和刪除操作的線性表。

我們把允許插入和刪除的一端稱為棧頂（top），另一端稱為棧底（bottom），不含任何數據元素的棧稱為空棧。棧又稱為后進先出（Last In First Out）的線性表，簡稱LIFO結構。
在這里插入圖片描述

問題：最先進棧的元素,是不是就只能是最后出棧呢?

不一定。棧對線性表的插入和刪除的位置進行了限制，并沒有對元素進出的時間進行限制，也就是說，在不是所有元素都進棧的情況下，事先進去的元素也可以出棧，只要保證是棧頂元素出棧就可以。

棧的抽象數據類型

對干棧來講，理論上線性表的操作特性它都具備，可由干它的特殊性，所以針對它在操作上會有些變化。特別是插入和刪除操作，我們改名為push和pop。
在這里插入圖片描述
由于棧本身就是一個線性表，因此線性表的順序存儲和鏈式存儲，對于棧來說，也是同樣適用。

棧的順序存儲結構及實現

棧是線性表的特例，因此棧的順序存儲也是線性表順序存儲的簡化，我們簡稱為順序棧。

線性表是用數組來實現的，用數組的下標0作為棧底比較好，因為首元素都會存在棧底，變化量小。

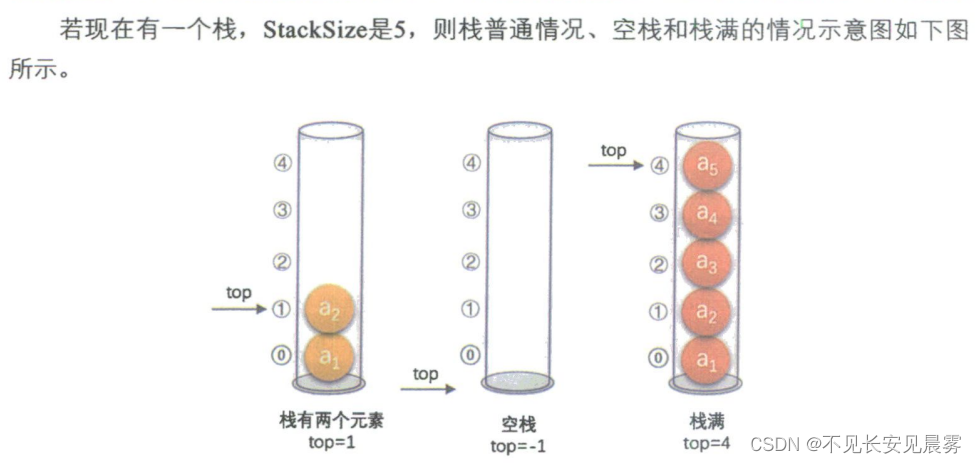
我們定義一個top變量來指示棧頂元素在數組中的位置，它可以來回移動，意味著棧頂的top可以變大變小，若存儲棧的長度為StackSize，則棧頂位置top必須小于StackSize。當棧存在—個元素時，top等于0，因此通常把空棧的判定條件定為top等于-1。
在這里插入圖片描述
在這里插入圖片描述

#include "stdio.h"    
#include "stdlib.h"   #include "math.h"  
#include "time.h"#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存儲空間初始分配量 */typedef int Status; 
typedef int SElemType; /* SElemType類型根據實際情況而定，這里假設為int *//* 順序棧結構 */
typedef struct
{SElemType data[MAXSIZE];int top; /* 用于棧頂指針 */
}SqStack;Status visit(SElemType c)
{printf("%d ",c);return OK;
}/*  構造一個空棧S */
Status InitStack(SqStack *S)
{ /* S.data=(SElemType *)malloc(MAXSIZE*sizeof(SElemType)); */S->top=-1;return OK;
}/* 把S置為空棧 */
Status ClearStack(SqStack *S)
{ S->top=-1;return OK;
}/* 若棧S為空棧，則返回TRUE，否則返回FALSE */
Status StackEmpty(SqStack S)
{ if (S.top==-1)return TRUE;elsereturn FALSE;
}/* 返回S的元素個數，即棧的長度 */
int StackLength(SqStack S)
{ return S.top+1;
}/* 若棧不空，則用e返回S的棧頂元素，并返回OK；否則返回ERROR */
Status GetTop(SqStack S,SElemType *e)
{if (S.top==-1)return ERROR;else*e=S.data[S.top];return OK;
}/* 插入元素e為新的棧頂元素 */
Status Push(SqStack *S,SElemType e)
{if(S->top == MAXSIZE -1) /* 棧滿 */{return ERROR;}S->top++;				/* 棧頂指針增加一 */S->data[S->top]=e;  /* 將新插入元素賦值給棧頂空間 */return OK;
}/* 若棧不空，則刪除S的棧頂元素，用e返回其值，并返回OK；否則返回ERROR */
Status Pop(SqStack *S,SElemType *e)
{ if(S->top==-1)return ERROR;*e=S->data[S->top];	/* 將要刪除的棧頂元素賦值給e */S->top--;				/* 棧頂指針減一 */return OK;
}/* 從棧底到棧頂依次對棧中每個元素顯示 */
Status StackTraverse(SqStack S)
{int i;i=0;while(i<=S.top){visit(S.data[i++]);}printf("\n");return OK;
}int main()
{int j;SqStack s;int e;if(InitStack(&s)==OK)for(j=1;j<=10;j++)Push(&s,j);printf("棧中元素依次為：");StackTraverse(s);Pop(&s,&e);printf("彈出的棧頂元素 e=%d\n",e);printf("棧空否：%d(1:空 0:否)\n",StackEmpty(s));GetTop(s,&e);printf("棧頂元素 e=%d 棧的長度為%d\n",e,StackLength(s));ClearStack(&s);printf("清空棧后，棧空否：%d(1:空 0:否)\n",StackEmpty(s));return 0;
}

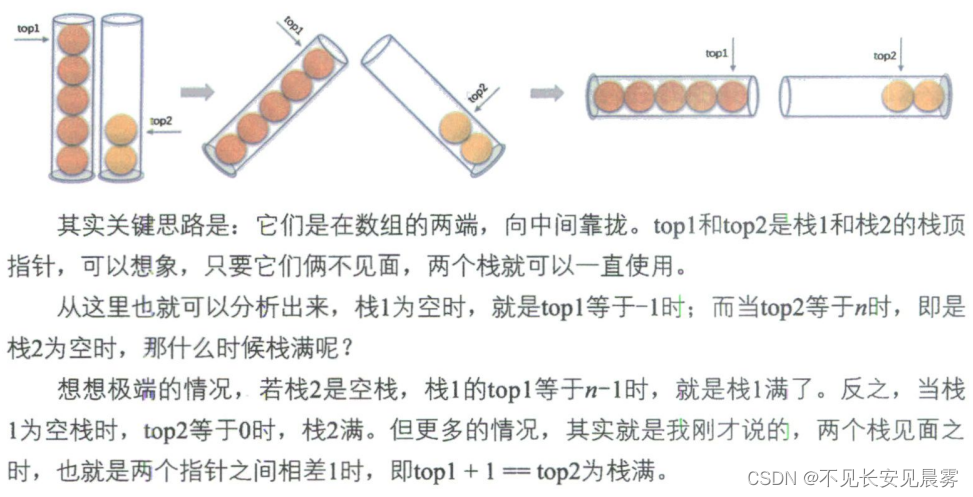
兩棧共享空間

前提：兩個棧中的數據類型相同
使用場景：通常是當兩個棧的空間需求有相反關系時，即一個棧增長時另一個棧在縮短。
在這里插入圖片描述

#include "stdio.h"    
#include "stdlib.h"   #include "math.h"  
#include "time.h"#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存儲空間初始分配量 */typedef int Status; typedef int SElemType; /* SElemType類型根據實際情況而定，這里假設為int *//* 兩棧共享空間結構 */
typedef struct 
{SElemType data[MAXSIZE];int top1;	/* 棧1棧頂指針 */int top2;	/* 棧2棧頂指針 */
}SqDoubleStack;Status visit(SElemType c)
{printf("%d ",c);return OK;
}/*  構造一個空棧S */
Status InitStack(SqDoubleStack *S)
{ S->top1=-1;S->top2=MAXSIZE;return OK;
}/* 把S置為空棧 */
Status ClearStack(SqDoubleStack *S)
{ S->top1=-1;S->top2=MAXSIZE;return OK;
}/* 若棧S為空棧，則返回TRUE，否則返回FALSE */
Status StackEmpty(SqDoubleStack S)
{ if (S.top1==-1 && S.top2==MAXSIZE)return TRUE;elsereturn FALSE;
}/* 返回S的元素個數，即棧的長度 */
int StackLength(SqDoubleStack S)
{ return (S.top1+1)+(MAXSIZE-S.top2);
}/* 插入元素e為新的棧頂元素 */
Status Push(SqDoubleStack *S,SElemType e,int stackNumber)
{if (S->top1+1==S->top2)	/* 棧已滿，不能再push新元素了 */return ERROR;	if (stackNumber==1)			/* 棧1有元素進棧 */S->data[++S->top1]=e; /* 若是棧1則先top1+1后給數組元素賦值。 */else if (stackNumber==2)	/* 棧2有元素進棧 */S->data[--S->top2]=e; /* 若是棧2則先top2-1后給數組元素賦值。 */return OK;
}/* 若棧不空，則刪除S的棧頂元素，用e返回其值，并返回OK；否則返回ERROR */
Status Pop(SqDoubleStack *S,SElemType *e,int stackNumber)
{ if (stackNumber==1) {if (S->top1==-1) return ERROR; /* 說明棧1已經是空棧，溢出 */*e=S->data[S->top1--]; /* 將棧1的棧頂元素出棧 */}else if (stackNumber==2){ if (S->top2==MAXSIZE) return ERROR; /* 說明棧2已經是空棧，溢出 */*e=S->data[S->top2++]; /* 將棧2的棧頂元素出棧 */}return OK;
}Status StackTraverse(SqDoubleStack S)
{int i;i=0;while(i<=S.top1){visit(S.data[i++]);}i=S.top2;while(i<MAXSIZE){visit(S.data[i++]);}printf("\n");return OK;
}int main()
{int j;SqDoubleStack s;int e;if(InitStack(&s)==OK){for(j=1;j<=5;j++)Push(&s,j,1);for(j=MAXSIZE;j>=MAXSIZE-2;j--)Push(&s,j,2);}printf("棧中元素依次為：");StackTraverse(s);printf("當前棧中元素有：%d \n",StackLength(s));Pop(&s,&e,2);printf("彈出的棧頂元素 e=%d\n",e);printf("棧空否：%d(1:空 0:否)\n",StackEmpty(s));for(j=6;j<=MAXSIZE-2;j++)Push(&s,j,1);printf("棧中元素依次為：");StackTraverse(s);printf("棧滿否：%d(1:否 0:滿)\n",Push(&s,100,1));ClearStack(&s);printf("清空棧后，棧空否：%d(1:空 0:否)\n",StackEmpty(s));return 0;
}

棧的鏈式存儲結構及實現

棧的鏈式存儲結構，簡稱為鏈棧。

棧只是棧頂來做插入和刪除操作，棧頂應該在鏈表的頭部還是尾部呢？由于單鏈表有頭指針，而棧頂指針也是必需的，所以好的辦法是把棧頂放在單鏈表的頭部。

因為已經有棧頂在頭部了，所以單鏈表中的頭結點也就失去了意義，通常對于鏈棧來說，是不需要頭結點的。

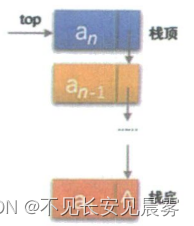
在這里插入圖片描述
對于空棧來說，鏈表原定義是頭指針指向空，那么鏈棧的空其實就是top＝NULL的時候。
在這里插入圖片描述

#include "stdio.h"    
#include "stdlib.h"   #include "math.h"  
#include "time.h"#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存儲空間初始分配量 */typedef int Status; 
typedef int SElemType; /* SElemType類型根據實際情況而定，這里假設為int *//* 鏈棧結構 */
typedef struct StackNode
{SElemType data;struct StackNode *next;
}StackNode,*LinkStackPtr;typedef struct
{LinkStackPtr top;int count;
}LinkStack;Status visit(SElemType c)
{printf("%d ",c);return OK;
}/*  構造一個空棧S */
Status InitStack(LinkStack *S)
{ S->top = (LinkStackPtr)malloc(sizeof(StackNode));if(!S->top)return ERROR;S->top=NULL;S->count=0;return OK;
}/* 把S置為空棧 */
Status ClearStack(LinkStack *S)
{ LinkStackPtr p,q;p=S->top;while(p){  q=p;p=p->next;free(q);} S->count=0;return OK;
}/* 若棧S為空棧，則返回TRUE，否則返回FALSE */
Status StackEmpty(LinkStack S)
{ if (S.count==0)return TRUE;elsereturn FALSE;
}/* 返回S的元素個數，即棧的長度 */
int StackLength(LinkStack S)
{ return S.count;
}/* 若棧不空，則用e返回S的棧頂元素，并返回OK；否則返回ERROR */
Status GetTop(LinkStack S,SElemType *e)
{if (S.top==NULL)return ERROR;else*e=S.top->data;return OK;
}/* 插入元素e為新的棧頂元素 */
Status Push(LinkStack *S,SElemType e)
{LinkStackPtr s=(LinkStackPtr)malloc(sizeof(StackNode)); s->data=e; s->next=S->top;	/* 把當前的棧頂元素賦值給新結點的直接后繼，見圖中① */S->top=s;         /* 將新的結點s賦值給棧頂指針，見圖中② */S->count++;return OK;
}/* 若棧不空，則刪除S的棧頂元素，用e返回其值，并返回OK；否則返回ERROR */
Status Pop(LinkStack *S,SElemType *e)
{ LinkStackPtr p;if(StackEmpty(*S))return ERROR;*e=S->top->data;p=S->top;					/* 將棧頂結點賦值給p，見圖中③ */S->top=S->top->next;    /* 使得棧頂指針下移一位，指向后一結點，見圖中④ */free(p);                    /* 釋放結點p */        S->count--;return OK;
}Status StackTraverse(LinkStack S)
{LinkStackPtr p;p=S.top;while(p){visit(p->data);p=p->next;}printf("\n");return OK;
}int main()
{int j;LinkStack s;int e;if(InitStack(&s)==OK)for(j=1;j<=10;j++)Push(&s,j);printf("棧中元素依次為：");StackTraverse(s);Pop(&s,&e);printf("彈出的棧頂元素 e=%d\n",e);printf("棧空否：%d(1:空 0:否)\n",StackEmpty(s));GetTop(s,&e);printf("棧頂元素 e=%d 棧的長度為%d\n",e,StackLength(s));ClearStack(&s);printf("清空棧后，棧空否：%d(1:空 0:否)\n",StackEmpty(s));return 0;
}

順序棧與鏈棧對比

對比一下順序棧與鏈棧，它們在時間復雜度上是一樣的，均為O(1)。對于空間性能，順序棧需要事先確定一個固定的長度，可能會存在內存空間浪費的問題，但它的優勢是存取時定位很方便，而鏈棧則要求每個元素都有指針域，這同時也增加了—些內存開銷，但對于棧的長度無限制。

所以它們的區別和線性表—樣，如果棧的使用過程中元素變化不可預料，有時很小，有時非常大，那么最好是用鏈棧。反之，如果它的變化在可控范圍內，建議使用順序棧會更好一些。

棧的作用

棧的引入簡化了程序設計的問題，劃分了不同關注層次，使得思考范圍縮小，更加聚焦于我們要解決的問題核心。

而像線性表順序存儲結構用到的數組，因為要分散精力去考慮數組的下標增減等細節問題反而掩蓋了問題的本質。

棧的應用——遞歸

斐波那契數列

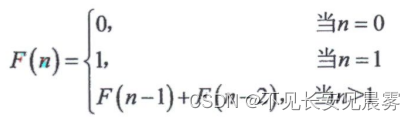
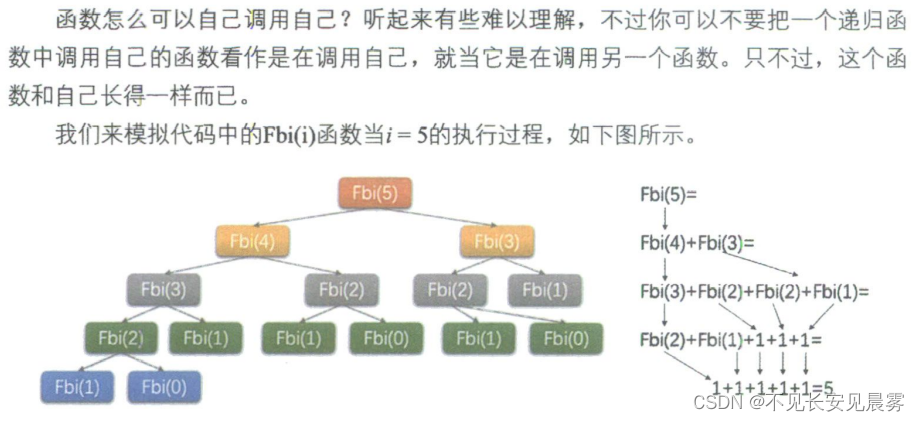
在這里插入圖片描述
在這里插入圖片描述

#include "stdio.h"/* 斐波那契的遞歸函數 */
int Fbi(int i)  
{if( i < 2 )return i == 0 ? 0 : 1;  return Fbi(i - 1) + Fbi(i - 2);  /* 這里Fbi就是函數自己，等于在調用自己 */
}  int main()
{int i;int a[40];  printf("迭代顯示斐波那契數列：\n");a[0]=0;a[1]=1;printf("%d ",a[0]);  printf("%d ",a[1]);  for(i = 2;i < 40;i++)  { a[i] = a[i-1] + a[i-2];  printf("%d ",a[i]);  } printf("\n");printf("遞歸顯示斐波那契數列：\n");for(i = 0;i < 40;i++)  printf("%d ", Fbi(i));  return 0;
}

迭代和遞歸的區別是：迭代使用的是循環結構，遞歸使用的是選擇結構。遞歸能使程序的結構更清晰、更簡潔、更容易讓人理解，從而減少讀懂代碼的時間。但是大量的遞歸調用會建立函數的副本，會耗費大量的時間和內存。迭代則不需要反復調用函數和占用額外的內存。因此我們應該視不同情況選擇不同的代碼實現方式。

遞歸過程退回的順序是它前行順序的逆序。在退回過程中，可能要執行某些動作，包括恢復在前行過程中存儲起來的某些數據。

這種存儲某些數據，并在后面又以存儲的逆序恢復這些數據，以提供之后使用的需求，顯然很符臺棧這樣的數據結構，因此，編譯器使用棧實現遞歸就沒什么好驚訝的了。

簡單地說，就是在前行階段，對于每一層遞歸，函數的局部變量、參數值以及返回地址都被壓入棧中。在退回階段，位于棧頂的局部變量、參數值和返回地址被彈出，用于返回調用層次中執行代碼的其余部分，也就是恢復了調用的狀態。

當然，對于現在的高級語言，這樣的遞歸問題是不需要用戶來管理這個棧的，一切都由系統代勞了。

棧的應用—四則運算表達式求值

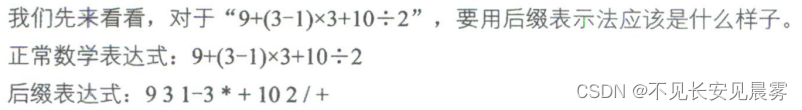
在這里插入圖片描述
"9 3 1 -3 *＋10 2／＋”，這樣的表達式稱為后綴表達式，叫后綴的原因在于所有的符號都是在要運算數字的后面出現。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/35083.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/35083.shtml
英文地址，請注明出處：http://en.pswp.cn/news/35083.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

VBA技術資料MF42：VBA_從Excel中上面的單元格復制公式

VBA技術資料MF42：VBA_從Excel中上面的單元格復制公式

【分享成果&#xff0c;隨喜正能量】唯有夢想才配讓你不安&#xff0c;唯有行動才能解除你的不安.繩鋸木斷&#xff0c;水滴石穿。也許你現在做的事情很小&#xff0c;只要你能日積月累的堅持下去&#xff0c;才會發現意義非凡。所謂的成功&#xff0c;便是別人失敗的時候你還在…
閱讀更多...
微服務與Nacos概述-2

微服務與Nacos概述-2

微服務間消息傳遞 微服務是一種軟件開發架構&#xff0c;它將一個大型應用程序拆分為一系列小型、獨立的服務。每個服務都可以獨立開發、部署和擴展&#xff0c;并通過輕量級的通信機制進行交互。 應用開發 common模塊中包含服務提供者和服務消費者共享的內容 provider模塊是…
閱讀更多...
10-1_Qt 5.9 C++開發指南_Data Visualization實現數據三維顯示

10-1_Qt 5.9 C++開發指南_Data Visualization實現數據三維顯示

Data Visualization 是 Qt 提供的用于數據三維顯示的模塊。在 Qt 5.7 以前只有商業版才有此模塊&#xff0c;而從Qt5.7 開始此模塊在社區版本里也可以免費使用了。Data Visualization 用于數據的三維顯示&#xff0c;包括三維柱狀圖、三維空間散點、三維曲面等。Data Visualiza…
閱讀更多...
鑒源實驗室丨汽車網絡安全攻擊實例解析（二）

鑒源實驗室丨汽車網絡安全攻擊實例解析（二）

作者 | 田錚 上海控安可信軟件創新研究院項目經理 來源 | 鑒源實驗室 社群 | 添加微信號“TICPShanghai”加入“上海控安51fusa安全社區” 引言&#xff1a;汽車信息安全事件頻發使得汽車行業安全態勢愈發緊張。這些汽車網絡安全攻擊事件&#xff0c;輕則給企業產品發布及產品…
閱讀更多...
高效數據傳輸：輕松上手將Kafka實時數據接入CnosDB

高效數據傳輸：輕松上手將Kafka實時數據接入CnosDB

本篇我們將主要介紹如何在 Ubuntu 22.04.2 LTS 環境下&#xff0c;實現一個KafkaTelegrafCnosDB 同步實時獲取流數據并存儲的方案。在本次操作中&#xff0c;CnosDB 版本是2.3.0&#xff0c;Kafka 版本是2.5.1&#xff0c;Telegraf 版本是1.27.1 隨著越來越多的應用程序架構轉…
閱讀更多...
無涯教程-Perl - redo函數

無涯教程-Perl - redo函數

描述 此函數將重新啟動當前循環,而不會強制判斷控制語句。塊中不再執行任何語句。如果存在繼續塊,將不會執行。如果指定了LABEL,則在LABEL標識的循環開始時重新開始執行。 語法 以下是此函數的簡單語法- redo LABELredo返回值 此函數不返回任何值。 例 以下是顯示其基本…
閱讀更多...
用友時空KSOA SQL注入漏洞復現（HW0day）

用友時空KSOA SQL注入漏洞復現（HW0day）

0x01 產品簡介 用友時空KSOA是建立在SOA理念指導下研發的新一代產品&#xff0c;是根據流通企業最前沿的I需求推出的統一的IT基礎架構&#xff0c;它可以讓流通企業各個時期建立的IT系統之間彼此輕松對話&#xff0c;幫助流通企業保護原有的IT投資&#xff0c;簡化IT管理&#…
閱讀更多...
以商業大數據技術助力數據合規流通體系建立，合合信息參編《數據經紀從業人員評價規范》團標

以商業大數據技術助力數據合規流通體系建立，合合信息參編《數據經紀從業人員評價規范》團標

經國務院批準&#xff0c;由北京市人民政府、國家發展和改革委員會、工業和信息化部、商務部、國家互聯網信息辦公室、中國科學技術協會共同主辦的2023 全球數字經濟大會于近期隆重召開。由數交數據經紀&#xff08;深圳&#xff09;有限公司為主要發起單位&#xff0c;合合信息…
閱讀更多...
深度剖析堆棧指針

深度剖析堆棧指針

為什么打印root的值與&root->value的值是一樣的呢 測試結果&#xff1a; *號一個變量到底取出來的是什么&#xff1f; 以前我寫過一句話&#xff0c;就是說&#xff0c;如果看到一個*變量&#xff0c;那就是直逼這個變量所保存的內存地址&#xff0c;然后取出里面保存的…
閱讀更多...
Skeleton-Aware Networks for Deep Motion Retargeting

Skeleton-Aware Networks for Deep Motion Retargeting

Skeleton-Aware Networks for Deep Motion Retargeting解析 摘要1. 簡介2. Related Work2.1 運動重定向&#xff08;Motion Retargeting&#xff09;2.2 Neural Motion Processing 3. 概述&#xff08;Overview&#xff09;4. 骨骼感知深度運動處理4.1 運動表征4.2 骨架卷積4.3…
閱讀更多...
Spring Boot + Vue3前后端分離實戰wiki知識庫系統＜十二＞--用戶管理單點登錄開發一

Spring Boot + Vue3前后端分離實戰wiki知識庫系統＜十二＞--用戶管理單點登錄開發一

目標&#xff1a; 在上一次Spring Boot Vue3前后端分離實戰wiki知識庫系統&#xff1c;十一&#xff1e;--文檔管理功能開發三我們已經完成了文檔管理的功能模塊開發&#xff0c;接下來則開啟新模塊的學習---用戶登錄&#xff0c;這塊還是有不少知識點值得學習的&#xff0c;…
閱讀更多...
指針與引用：C語言中的內存魔法

指針與引用：C語言中的內存魔法

開始本篇文章之前先推薦一個好用的學習工具&#xff0c;AIRIght&#xff0c;借助于AI助手工具&#xff0c;學習事半功倍。歡迎訪問&#xff1a;http://airight.fun/。 也把我學習過程中搜集的資料分享給大家&#xff0c;希望可以幫助大家少走彎路&#xff0c;鏈接&#xff1a;h…
閱讀更多...
機器人CPP編程基礎-02變量Variables

機器人CPP編程基礎-02變量Variables

機器人CPP編程基礎-01第一個程序Hello World 基礎代碼都可以借助人工智能工具進行學習。 C #include<iostream>using namespace std;main() {//Declaring an integer type variable A, allocates 4 bytes of memory.int A4;cout<<A <<endl;//Prints the a…
閱讀更多...
Matlab繪制圓形（rectangle函數、viscircles函數和圓的參數方程）

Matlab繪制圓形（rectangle函數、viscircles函數和圓的參數方程）

基于matlab繪制圓形 一、rectangle函數 對于繪制圓心坐標為&#xff08;x&#xff0c;y&#xff09;半徑為r的圓形&#xff0c;函數為&#xff1a; x0; y0; r1; rectangle(Position, [x-r,y-r,2*r,2*r], Curvature, [1 1],EdgeColor, r); axis equalEdgeColor表示顏色 二、…
閱讀更多...
多版本node環境搭建切換管理NVM

多版本node環境搭建切換管理NVM

Node.js NVM 全名 Node Version Management 一、Node 模塊對象 參考博客 Node 模塊對象 二、Node 多版本管理NVM &#xff08;1&#xff09;參考 Node 多版本管理 &#xff08;2&#xff09;github上NVM工具 nvm-windows mirrors / coreybutler / nvm-windows GitCode…
閱讀更多...
消息隊列(12) - 定義服務器類

消息隊列(12) - 定義服務器類

目錄 前言設計思想 前言 之前,我們寫了通信協議的具體設計,接下來我們設計服務器類 設計思想 我們先只考慮一個虛擬主機的情況下, 在一個虛擬主機的情況下,我們需要有一個session會話來幫助我們存儲信息,并且既然是網絡通信,那么socket關鍵字肯定也必不可少,我們在引入一個線…
閱讀更多...
解決lldb調試時可能出現的personality set failed: Function not implemented

解決lldb調試時可能出現的personality set failed: Function not implemented

最近在嘗試使用Visual Studio 2022遠程連接Linux進行C/C的開發&#xff0c;由于CentOS風波不斷&#xff0c;所以現在的開發基本上都是使用ubuntu了&#xff0c;但是目前VS2022有一些BUG&#xff0c;就是遠程調試時&#xff0c;如果目標系統是ubuntu則會出現啟動調試器很慢的問題…
閱讀更多...
mysql高并發下主鍵自增打來的問題

mysql高并發下主鍵自增打來的問題

在一般情況下&#xff0c;在新增領域對象后&#xff0c;都需要獲取對應的主鍵值。使用應用層來維護主鍵&#xff0c;在一定程度上有利于程序性能的優化和應用移植性的提高。在采用數據庫自增主鍵的方案里&#xff0c;如果JDBC驅動不能綁定新增記錄對應的主鍵&#xff0c;就需要…
閱讀更多...
LeetCode 1281. 整數的各位積和之差

LeetCode 1281. 整數的各位積和之差

【LetMeFly】1281.整數的各位積和之差 力扣題目鏈接&#xff1a;https://leetcode.cn/problems/subtract-the-product-and-sum-of-digits-of-an-integer/ 給你一個整數 n&#xff0c;請你幫忙計算并返回該整數「各位數字之積」與「各位數字之和」的差。 示例 1&#xff1a; …
閱讀更多...
學習筆記整理-JS-03-表達式和運算符

學習筆記整理-JS-03-表達式和運算符

[[toc]] 一、表達式和運算符 1. 表達式 表達式種類 算術、關系、邏輯、賦值、綜合 二、JS基本表達式 1. 算術運算符 意義運算符加減-乘*除/取余% 加減乘除 加減的符號和數學一致&#xff0c;乘號是*號&#xff0c;除法是/號默認情況&#xff0c;乘除法的優先級高于加法和…
閱讀更多...
最新文章

Copyright @ 2022~2023