AOE關鍵路徑編程

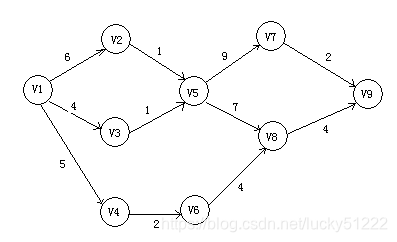
不難發現AOE圖最大特點是沒有回路，并且有向圖方向始終是從源點走向匯點，且源點匯點都是一個。

把圖1寫成鄰接矩陣文件，見文件P200G736.TXT，并在此復制G0.C到AOE.C，修改這個程序的讀文件名稱，使其正確讀出該文件的數據并構造圖。

分析圖1可知，該圖實際有以下路徑：

V1->V2->V5->V7->V9;
V1->V3->V5->V7->V9;
V1->V2->V5->V8->V9;
V1->V3->V5->V8->V9;
V1->V4->V6->V8->V9;

一共是5條路徑，這5條路徑上面的權值和最大者就是關鍵路徑。

很明顯，把上述5條路徑的V1合并成一個結點，則可以看這個結果實際是一個生成樹，這個生成樹上的結點或許是重復的，但要全部走完，則結果肯定是這樣的一棵樹，這樣的樹我們這里成為全路徑生成樹，或許N多教材沒這個稱謂，但要編程求解該問題則必然是要先解出該樹來、然后累計求和每個子樹上的權值和。

C#的程序上很容易做到這個樹，這個解就是：

這樣的樹，實際是一種特殊的深度優先遍歷生成的結果。

回顧我們在普通的圖上做的深度優先遍歷，由于一般意義上的圖中存在回路，所以我們需要一個Visited[]這樣的數組、標記已經走過的頂點，從而制止了在一個回路上無限循環，但我們分析AOE圖則不難發現：我們不需要標記已經走過的頂點，深度優先遍歷也可以順利從源點到匯點走完。

手工完成這樣的遍歷不是問題，所以我們可以編寫出以下的程序來遍歷：

void AOETrav (struct Graph *G,int n)
{int i;if(G==NULL) return;printf("%d\t%s\n",n,G->pV[n]);for(i=0;i<G->num;i++)if(G->pA[n][i]!=0)AOETrav(G,i);
}

對照我們前面的深度優先遍歷函數：

void DFS(struct Graph *G,int n)
{int i;if(G==NULL) return;if(n<0||n>G->num) return;G->Visited[n]=1;printf("%s ",G->pV[n]); for(i=0;i<G->num;i++)if(G->pA[n][i]!=0&&G->Visited[i]!=1) 
DFS(G,i);
}

執行AOE1.c程序，則結果是：

V1、 V2、V5、V7、 V9、V8、V9、V3、V5、V7、V9、 V8、V9、V4、V6、V8、V9  

分析表1的程序以及結果不難發現：

<1> 如AOETrav( )函數入口參數n是生成樹父結點的話、那么在第8行進入下一個頂點時所找到的第i個頂點、則就是第n個結點的孩子；

<2> 如果設到第n個結點的權值累計合是w，則該函數就是這樣的入口參數：

void AOETrav (struct Graph *G,int n,int w)

有這樣的函數后，則在表1的第9行就是：

AOETrav(G,i, w+G->pA[n][i]);

也就是說：到第n個頂點的權值如果是w的話，則到第n個后的第i個頂點，其權值合計是:

w+A[n][i];

然后，我們設計一個雙親表示法的表格，按：

void AOETrav (struct Graph *G,int n,int w)
{int i,nw;if(G==NULL) return;for(i=0;i<G->num;i++)if(G->pA[n][i]!=0){nw=w+G->pA[n][i]; printf("%d\t%d\t%s\t%d\n",i,n,G->pV[i],nw);AOETrav(G,i,nw);}
}

修改main()函數，使其從第0個頂點開始，就是：

main()
{int i,j;struct Stack *S;struct Graph *G;G=GraphCreat("p200G736.txt");printf("頂點名稱:\n");for(i=0;i<G->num;i++)printf("%s\t",G->pV[i]);printf("\n鄰接矩陣:\n");for(i=0;i<G->num;i++) {for(j=0;j<G->num;j++)printf("%d\t",G->pA[i][j]);printf("\n");}printf("\n");printf("ID\tPID\tV\tW\n");printf("%d\t%d\t%s\t%d\n",0,-1,G->pV[0],0);AOETrav(G,0,0);
}

運行這個程序，會有以下結果：

至此，AOE的問題基本解決，查看表6，其最大權值是18，見上表第4行、第6行，如是第4行，則是V9，回溯PID=6到第3行V7、從V7取PID=4回到第2行V5、再從PID=1回到V2、從V2取PID=0回到V1，全路程就是：

V1、V2、V5、V7、V9，全路程權值合計是18

同理在第6行也有一條路徑：

V1、V3、V5、V8、V9，全路程權值和也是18，這也是一條關鍵路徑。

表6需要注意的是：由于這個樹上、一個結點可能出現在好幾個子樹上，所以父結點編號要尋找上面最近的結點編號。

AOE完整求解程序

上述解法、對小的AOE圖是可行的，但在大的圖上，很明顯對表6也需要進行編程處理，所以一個完整的AOE處理程序，還需要設計一個順序表、保存表6的結果，然后通過順序表求解出完整的計算結果。這個工作就留給同學們自己解決。

AOE2.c是通過一種簡單的方式、把各個路徑上的權值累計合計和路徑顯示出來的程序，請同學們自己分析。