1965 年，Bresenham 為數字繪圖儀開發了一種繪制直線的算法，該算法同樣使用于光柵掃描顯示器，被稱為 Bresenham 算法。

原理

算法的目標是選擇表示直線的最佳光柵位置。Bresenhan 算法在主位移方向上每次遞增一個單位。另一個方向的增量為 0 或 1，取決于理想直線于最近網格點的距離，這一距離稱為誤差項，誤差項用 d 表示。

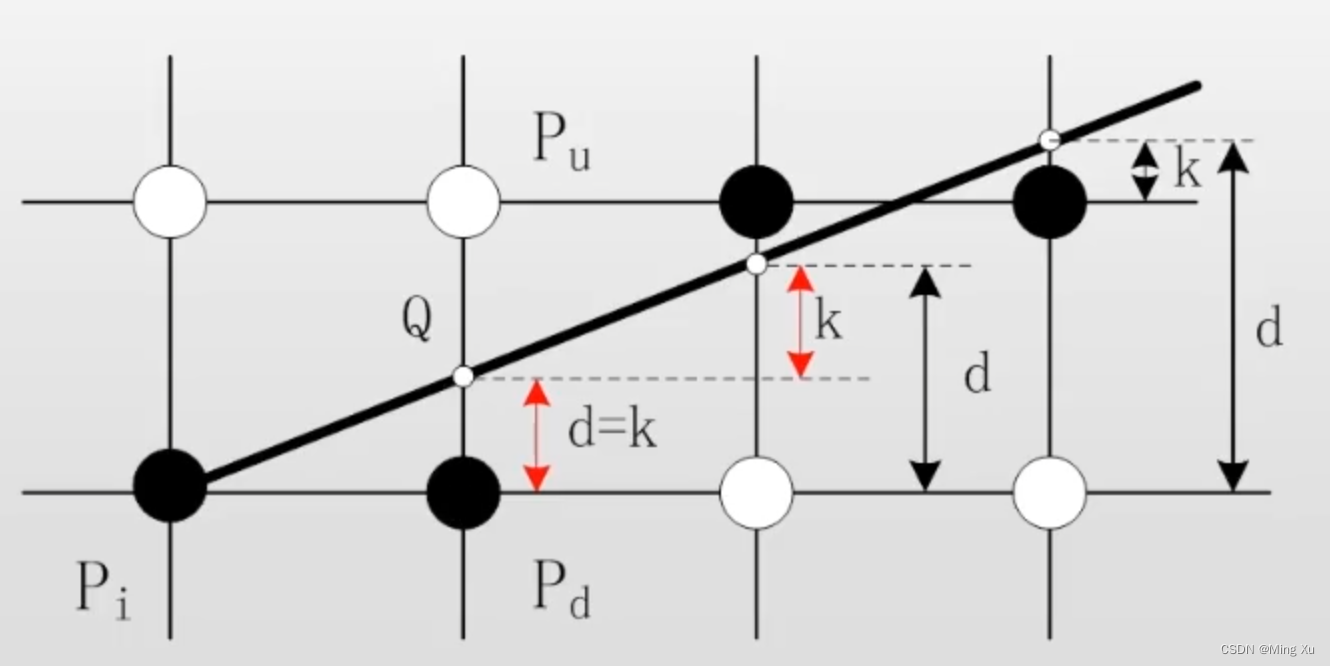
當 $x$ 方向遞增一個單位，有 $d=d+k$; 則

$$y_{i+1}=\{\begin{array}{ll}{y}_i+1;& d\ge 0.5\\ y_i& d<0.5\end{array}$$
誤差項初始值 $d_0=0$， 如果 $d\ge 0.5$， $y$ 方向遞增一個單位并且將 $d$ 減 1.

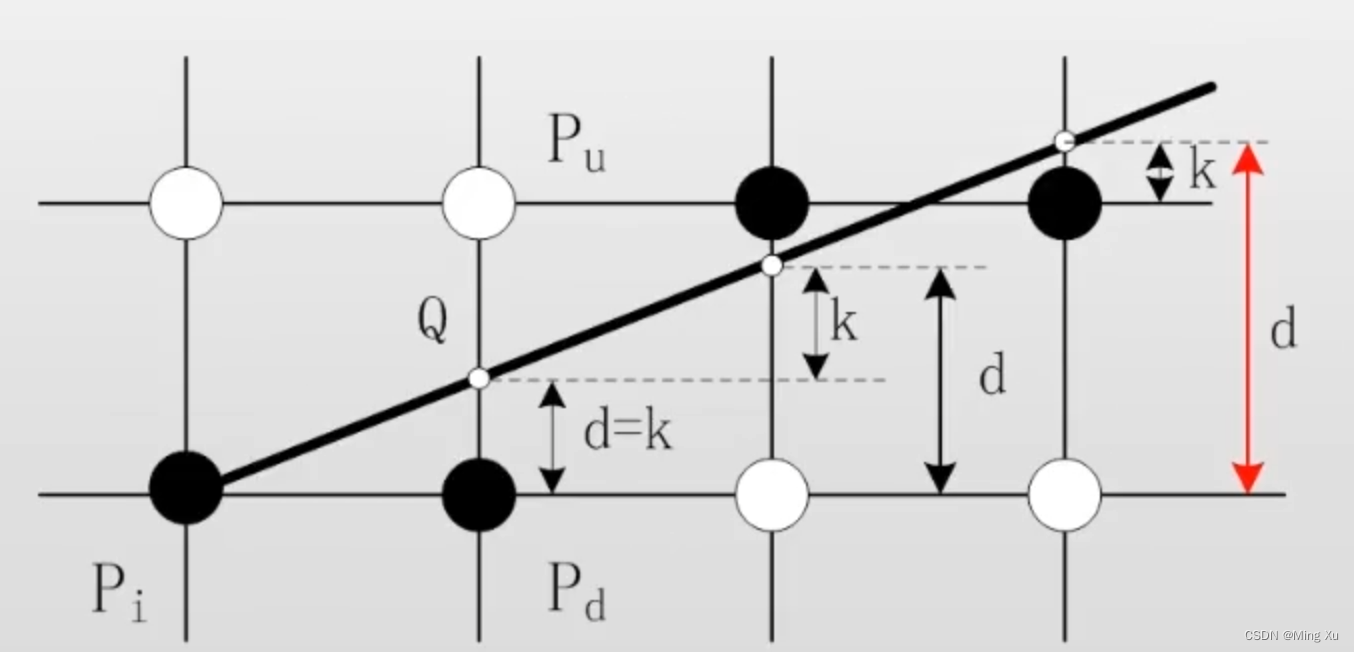
消除 0.5 的影響

令 $e=d?0.5$. 當 $x$ 方向走一步，有 $e=e+k$, 則

$$y_{i+1}=\{\begin{array}{ll}{y}_i+1;& e\ge 0\\ y_i& e<0.5\end{array}$$

$e_0=?0.5$ , 如果 $e\ge 0$, 則 $e=e?1$

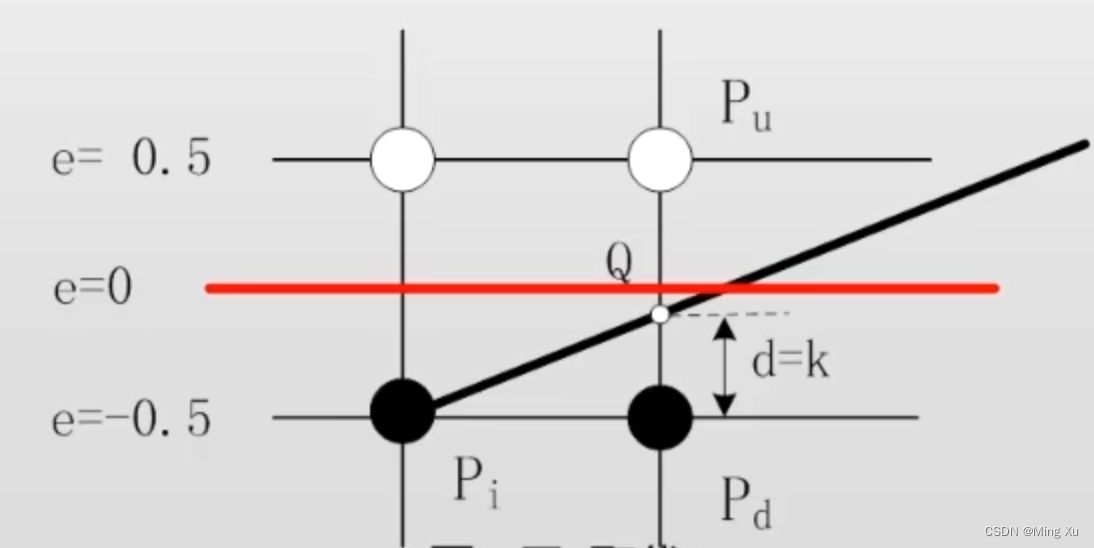
消除浮點數的影響，斜率和 $e$, 進行整數化

當 $0\le k\le 1$， $\Delta x$ 為正
$$e=2\Delta xe=2\Delta x(d?0.5)=?\Delta x+2\Delta xd$$
初始值 $e_0=?\Delta x$
當 x 方向走一步，有 $e+=2\Delta y$

如果 $e\ge 0$ 有

$$\begin{gathered} e=2\Delta x(e?1)=2\Delta xe?2\Delta x \\ e?=2\Delta x \end{gathered}$$

算法

• 設置像素點的顏色
• 讀入直線的兩個端點坐標
• 取 $e$ 的初始值為 $e_0=?0.5$
• 從起點開始，沿著 $x$ 軸方向每遞增一個單位，有 $e+=2\Delta y$
• 當 $\ge 0$ 時，下一個像素更新為 $(x_i+1,y_i+1)$, 同時將 $e$ 更新為 $e?=2\Delta x$, 否則，下一個像素更為 $(x_i+1,y_i+1)$
• 繪制像素點，執行 $x++$ 操作到終點

void BresenhamLine(CDC* pDC, CPoint P0, CPoint P1)
{COLORREF crColor = RGB(0, 0, 0);int dx = P1.x - P0.x;int dy = P1.y - P0.y;int e = - dx;for (int x=P0.x, y=P0.y; x < P1.x; x++) {pDC->SetPixelV(x, y, crColor);e += 2 * dy;if (e >= 0) {y++;e -= 2 * dx;}}
}

整數 Bresenham 算法是一種經典的直線光柵化算法, 使用了最小的計算量，使得單點生成算法已經沒有改進的余地。

參考 《計算幾何算法與實現》孔令德