題目:http://codeforces.com/contest/900/problem/D
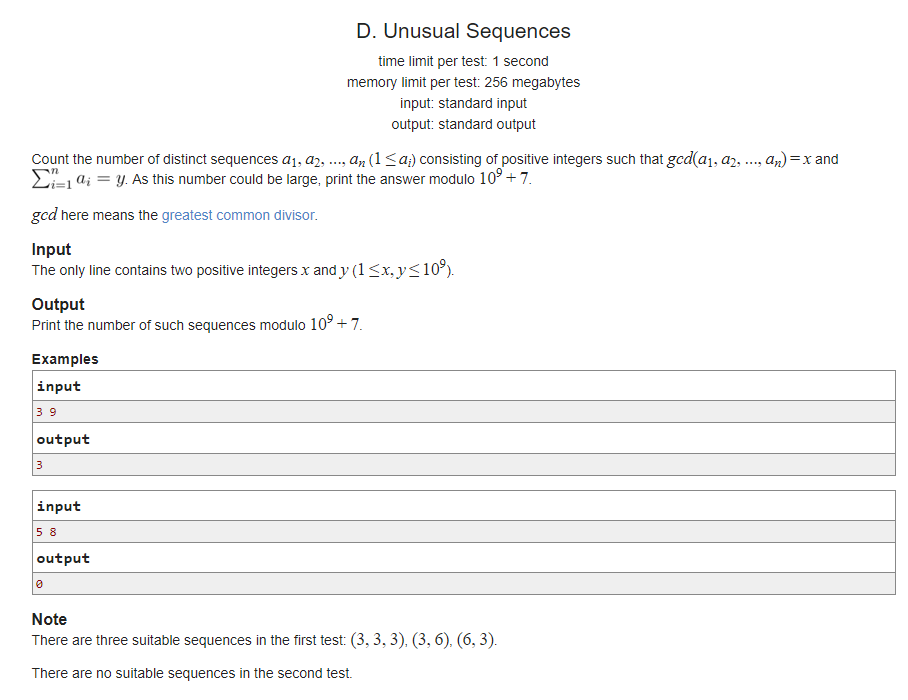
題意:找到加和為m的且gcd為n的數列種類數
分析:可以轉化為求gcd為1的加和為m/n的種類數,假設有m/n個1,則除了第一個以外的每個1可以選擇和前面一項合并,也可以獨立存在,故不考慮gcd總情況有$2^{(m/n-1)}$。
考慮過加和后,可以刪除gcd為2,3,4……的情況,gcd為2的情況則為2個相同的gcd為1且加和為n/2的序列組合,3同理。所以找出除1以外的所有x的因子,減去相應的情況,使用記憶化搜索。
代碼:
1 #define _CRT_SECURE_NO_DEPRECATE 2 #pragma comment(linker, "/STACK:102400000,102400000") 3 #include<iostream> 4 #include<cstdio> 5 #include<fstream> 6 #include<iomanip> 7 #include<algorithm> 8 #include<cmath> 9 #include<deque> 10 #include<vector> 11 #include<bitset> 12 #include<queue> 13 #include<string> 14 #include<cstring> 15 #include<map> 16 #include<stack> 17 #include<set> 18 #include<functional> 19 #define pii pair<int, int> 20 #define mod 1000000007 21 #define mp make_pair 22 #define pi acos(-1) 23 #define eps 0.00000001 24 #define mst(a,i) memset(a,i,sizeof(a)) 25 #define all(n) n.begin(),n.end() 26 #define lson(x) ((x<<1)) 27 #define rson(x) ((x<<1)|1) 28 #define inf 0x3f3f3f3f 29 typedef long long ll; 30 typedef unsigned long long ull; 31 using namespace std; 32 const int maxn = 1e5 + 5; 33 map<int, ll>dp; 34 ll poww(ll m, int n) 35 { 36 ll ans = 1; 37 ll temp = m%mod; 38 while (n) 39 { 40 if (n & 1) 41 ans *= temp; 42 ans %= mod; 43 temp *= temp; 44 temp %= mod; 45 n >>= 1; 46 } 47 return ans%mod; 48 } 49 ll getans(ll x) 50 { 51 if (dp.count(x))return dp[x]; 52 ll tempans = poww(2, x - 1); 53 for (int i = 2; i*i <= x; ++i) 54 { 55 if (x%i == 0)tempans = (tempans - getans(x / i) + mod) % mod; 56 if (x%i==0&&i*i != x)tempans = (tempans - getans(i) + mod) % mod; 57 } 58 tempans = (tempans - getans(1) + mod) % mod; 59 return dp[x]=tempans; 60 } 61 62 int main() 63 { 64 ios::sync_with_stdio(false); 65 cin.tie(0); cout.tie(0); 66 int i, j, k, m, n; 67 cin >> n >> m; 68 if (m%n) { cout << "0" << endl; return 0; } 69 dp[1] = 1; 70 m /= n; 71 ll ans = getans(m); 72 cout << ans << endl; 73 return 0; 74 }
















 功能,輕松限制請求數量)
)

