KMP算法配圖詳解
前言
KMP算法是我們數據結構串中最難也是最重要的算法。難是因為KMP算法的代碼很優美簡潔干練,但里面包含著非常深的思維。真正理解代碼的人可以說對KMP算法的了解已經相當深入了。而且這個算法的不少東西的確不容易講懂,很多正規的書本把概念一擺出直接勸退無數人。這篇文章將盡量以最詳細的方式配圖介紹KMP算法及其改進。文章的開始我先對KMP算法的三位創始人Knuth,Morris,Pratt致敬,懂得這個算法的流程后你真的不得不佩服他們的聰明才智。
KMP解決的問題類型
KMP算法的作用是在一個已知字符串中查找子串的位置,也叫做串的模式匹配。比如主串s=“goodgoogle”,子串t=“google”。現在我們要找到子串t 在主串s 中的位置。大家肯定覺得這還不簡單,不就在第五個嘛,一眼就看出來了。
當然,在字符串非常少時,“肉眼觀察法”不失為一個好方法。但如果要你在一千行文本里找一個單詞,我想一般人都會數得崩潰吧。這就讓我想起來考試的時候,如果一兩道選擇題不會。這時候,“肉眼觀察法”可能效果不錯,但是如果好幾道大題不會呢?“肉眼觀察法”就絲毫不起效了。所以打鐵還需自身硬,我們把這種枯燥的事以一定的算法交給計算機處理。
第一種我們容易想到的就是暴力求解法。
這種方法也叫樸素的模式匹配:
簡單來說就是:從主串s 和子串t 的第一個字符開始,將兩字符串的字符一一比對,如果出現某個字符不匹配,主串回溯到第二個字符,子串回溯到第一個字符再進行一一比對。如果出現某個字符不匹配,主串回溯到第三個字符,子串回溯到第一個字符再進行一一比對…一直到子串字符全部匹配成功。
下面我們通過圖片展示這個過程:
豎直線表示相等,閃電線表示不等
第一個過程:子串“goo”部分與主串相等,'g’不等,結束比對,進行回溯。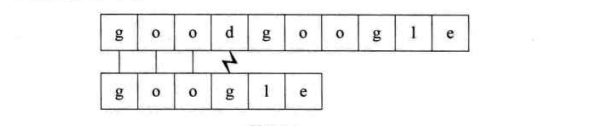
第二個過程:開始時就不匹配,直接回溯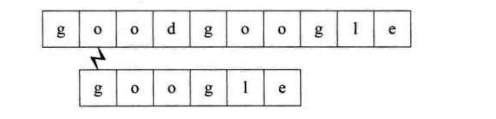
第三個過程:開始時即不匹配,直接回溯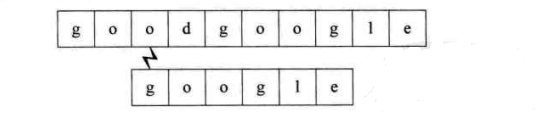
第四個過程:開始時即不匹配,直接回溯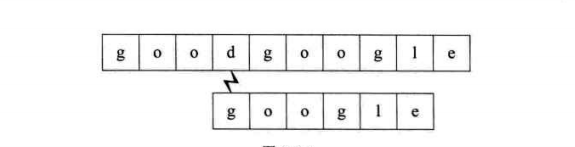
第五個過程:匹配成功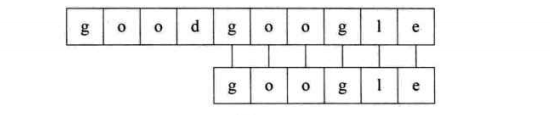
大家可能會想:這個方法也太慢了吧!求一個子串位置需要太多的步驟。而且很多步驟根本不必要進行。
這個想法非常好!!很多偉大的思想都是在一步步完善更正已有方法中誕生的。這種算法在最好情況下時間復雜度為O(n)。即子串的n個字符正好等于主串的前n個字符,而最壞的情況下時間復雜度為O(m*n)。相比而言這種算法空間復雜度為O(1),即不消耗空間而消耗時間。
下面就開始進入我們的正題:KMP算法是怎樣優化這些步驟的。其實KMP的主要思想是:“空間換時間”。
大家打起精神,認真看下面的內容。
首先,為什么樸素的模式匹配這么慢呢?
你再回頭看一遍就會發現,哦,原來是回溯的步驟太多了。所以我們應該盡量減少回溯的次數。
怎樣做呢?比如上面第一個圖:當字符’d’與’g’不匹配,我們保持主串的指向不變,
主串依然指向’d’,而把子串進行回溯,讓’d’與子串中’g’之前的字符再進行比對。
如果字符匹配,則主串和子串字符同時右移。
至于子串回溯到哪個字符,這個問題我們先放一放。
我先提出一個概念:一個字符串最長相等前綴和后綴。
教科書常用的手段是:在此處擺出一堆數學公式讓大家自行理解。
這也是為什么看計算機學科的書沒有較好的數學基礎會很痛苦。(當初我為什么不好好學數學T_T)
大家先不要強行理解數學公式,且聽我慢慢道來:
我給大家個例子。
字符串 abcdab
前綴的集合:{a,ab,abc,abcd,abcda}
后綴的集合:{b,ab,dab,cdab,bcdab}
那么最長相等前后綴不就是ab嘛.
做個小練習吧:
字符串:abcabfabcab中最長相等前后綴是什么呢:
對就是abcab
好了我們現在會求一個字符串的前綴,后綴以及最長相等前后綴了。
這個概念很重要。到這里如果都看懂了,可以鼓勵一下自己,然后回想一遍,再往下看。
之前留了一個問題,子串回溯到哪個字符,現在可以著手解決了。
圖解KMP
現在我們先看一個圖:第一個長條代表主串,第二個長條代表子串。紅色部分代表兩串中已匹配的部分,
綠色和藍色部分分別代表主串和子串中不匹配的字符。
再具體一些:這個圖代表主串"abcabeabcabcmn"和子串"abcabcmn"。
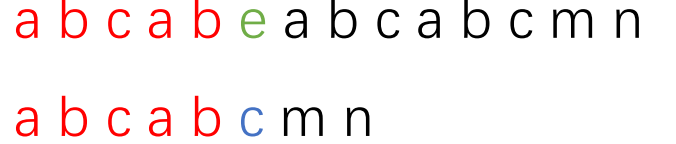
現在發現了不匹配的地方,根據KMP的思想我們要將子串向后移動,現在解決要移動多少的問題。
之前提到的最長相等前后綴的概念有用處了。因為紅色部分也會有最長相等前后綴。如下圖:
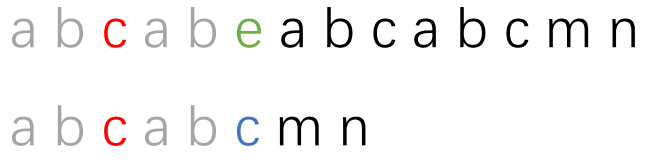
灰色部分就是紅色部分字符串的最長相等前后綴,我們子串移動的結果就是讓子串的紅色部分最長相等前綴和主串紅色部分最長相等后綴對齊。
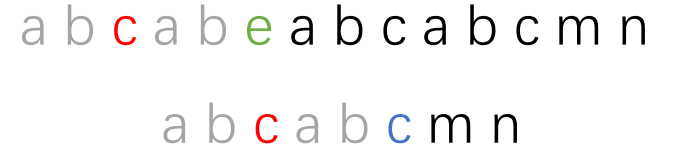
這一步弄懂了,KMP算法的精髓就差不多掌握了。接下來的流程就是一個循環過程了。事實上,每一個字符前的字符串都有最長相等前后綴,而且最長相等前后綴的長度是我們移位的關鍵,所以我們單獨用一個next數組存儲子串的最長相等前后綴的長度。而且next數組的數值只與子串本身有關。
所以next[i]=j,含義是:下標為i 的字符前的字符串最長相等前后綴的長度為j。
我們可以算出,子串t= "abcabcmn"的next數組為next[0]=-1(前面沒有字符串單獨處理)
next[1]=0;next[2]=0;next[3]=0;next[4]=1;next[5]=2;next[6]=3;next[7]=0;
| a | b | c | a | b | c | m | n |
|---|---|---|---|---|---|---|---|
| next[0] | next[1] | next[2] | next[3] | next[4] | next[5] | next[6] | next[7] |
| -1 | 0 | 0 | 0 | 1 | 2 | 3 | 0 |
本例中的藍色c處出現了不匹配(是s[5]!=t[5]),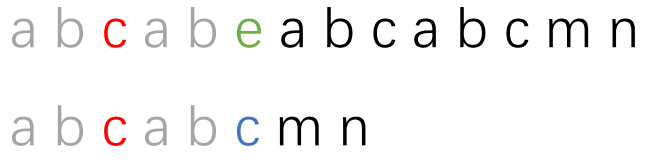
我們把子串移動,也就是讓s[5]與t[5]前面字符串的最長相等前綴后一個字符再比較,而該字符的位置就是t[?],很明顯這里的?是2,就是不匹配的字符前的字符串 最長相等前后綴的長度。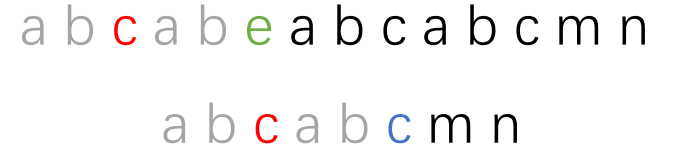
也是不匹配的字符處的next數組next[5]應該保存的值,也是子串回溯后應該對應的字符的下標。 所以?=next[5]=2。接下來就是比對是s[5]和t[next[5]]的字符。這里也是最奇妙的地方,也是為什么KMP算法的代碼可以那么簡潔優雅的關鍵。
我們可以總結一下,next數組作用有兩個:
一是之前提到的,
next[i]的值表示下標為i的字符前的字符串最長相等前后綴的長度。
二是:
表示該處字符不匹配時應該回溯到的字符的下標
next有這兩個作用的源頭是:之前提到的字符串的最長相等前后綴
想一想是不是覺得這個算法好厲害,從而不得不由衷佩服KMP算法的創始人們。
KMP算法的時間復雜度
現在我們分析一下KMP算法的時間復雜度:
KMP算法中多了一個求數組的過程,多消耗了一點點空間。我們設主串s長度為n,子串t的長度為m。求next數組時時間復雜度為O(m),因后面匹配中主串不回溯,比較次數可記為n,所以KMP算法的總時間復雜度為O(m+n),空間復雜度記為O(m)。相比于樸素的模式匹配時間復雜度O(m*n),KMP算法提速是非常大的,這一點點空間消耗換得極高的時間提速是非常有意義的,這種思想也是很重要的。
下面還有更厲害的,我們一起來分析具體的代碼。
求next數組的代碼
下面我們一起來欣賞計算機如何求得next數組的
typedef struct
{ char data[MaxSize];int length; //串長
} SqString;
//SqString 是串的數據結構
//typedef重命名結構體變量,可以用SqString t定義一個結構體。
void GetNext(SqString t,int next[]) //由模式串t求出next值
{int j,k;j=0;k=-1;next[0]=-1;//第一個字符前無字符串,給值-1while (j<t.length-1) //因為next數組中j最大為t.length-1,而每一步next數組賦值都是在j++之后//所以最后一次經過while循環時j為t.length-2{ if (k==-1 || t.data[j]==t.data[k]) //k為-1或比較的字符相等時{ j++;k++;next[j]=k;//對應字符匹配情況下,s與t指向同步后移//通過字符串"aaaaab"求next數組過程想一下這一步的意義//printf("(1) j=%d,k=%d,next[%d]=%d\n",j,k,j,k);}else{k=next[k];**//我們現在知道next[k]的值代表的是下標為k的字符前面的字符串最長相等前后綴的長度//也表示該處字符不匹配時應該回溯到的字符的下標//這個值給k后又進行while循環判斷,此時t.data[k]即指最長相等前綴后一個字符**//為什么要回退此處進行比較,我們往下接著看。其實原理和上面介紹的KMP原理差不多//printf("(2) k=%d\n",k);}}
}
解釋next數組構造過程中的回溯問題
大家來看下面的圖:
下面的長條代表子串,紅色部分代表當前匹配上的最長相等前后綴,藍色部分代表t.data[j]。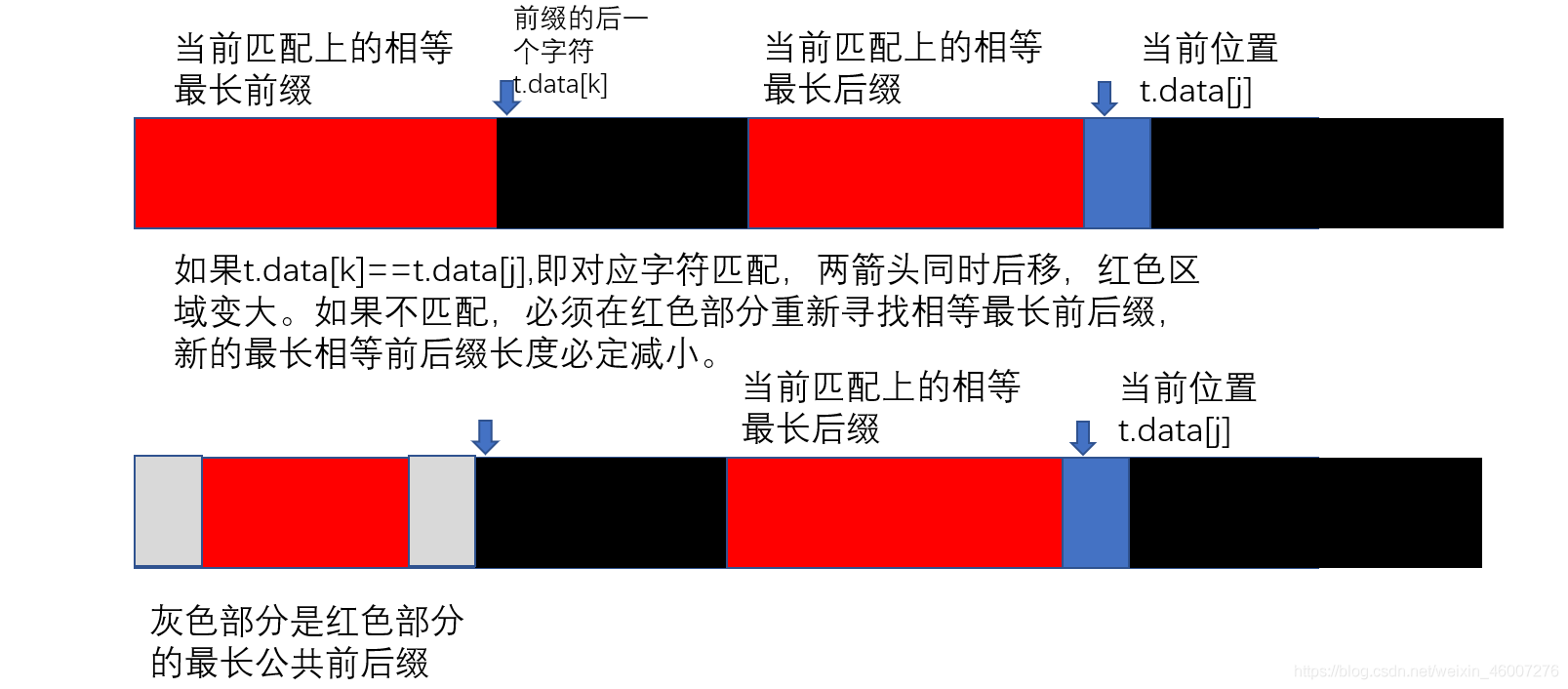
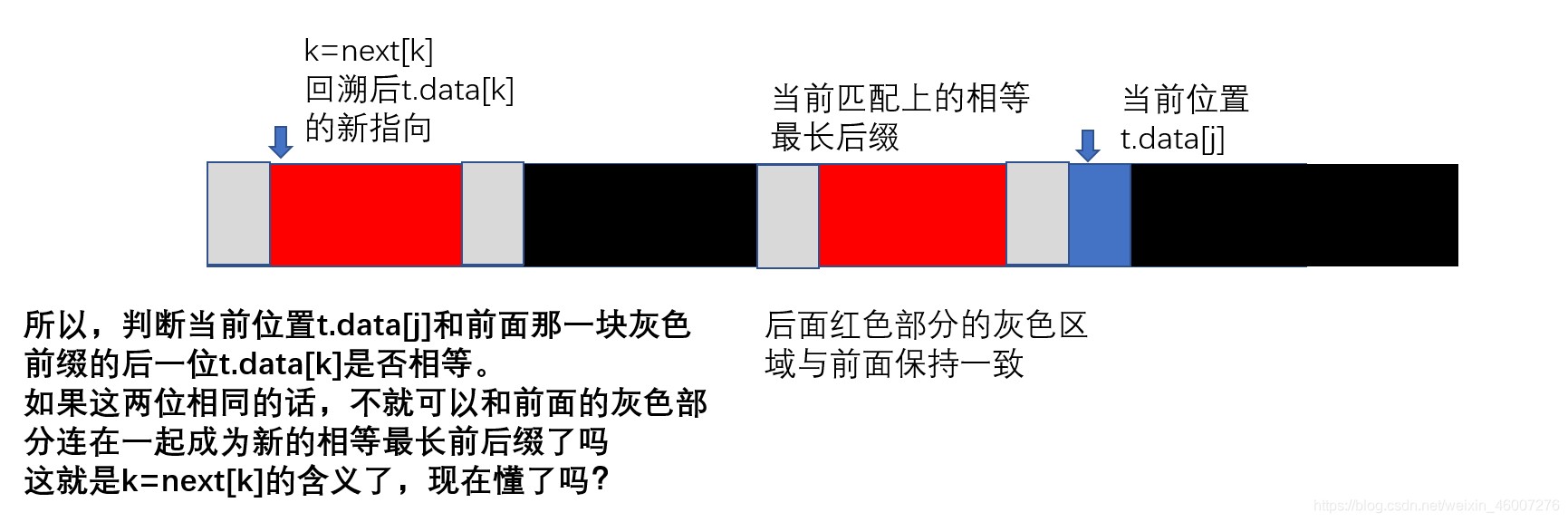
KMP算法代碼解釋
int KMPIndex(SqString s,SqString t) //KMP算法
{int next[MaxSize],i=0,j=0;GetNext(t,next);while (i<s.length && j<t.length) {if (j==-1 || s.data[i]==t.data[j]) {i++;j++; //i,j各增1}else j=next[j]; //i不變,j后退,現在知道為什么這樣讓子串回退了吧}if (j>=t.length)return(i-t.length); //返回匹配模式串的首字符下標else return(-1); //返回不匹配標志
}
KMP算法的改進
為什么KMP算法這么強大了還需要改進呢?
大家來看一個例子:
主串s=“aaaaabaaaaac”
子串t=“aaaaac”
這個例子中當‘b’與‘c’不匹配時應該‘b’與’c’前一位的‘a’比,這顯然是不匹配的。'c’前的’a’回溯后的字符依然是‘a’。
我們知道沒有必要再將‘b’與‘a’比對了,因為回溯后的字符和原字符是相同的,原字符不匹配,回溯后的字符自然不可能匹配。但是KMP算法中依然會將‘b’與回溯到的‘a’進行比對。這就是我們可以改進的地方了。我們改進后的next數組命名為:nextval數組。KMP算法的改進可以簡述為: 如果a位字符與它next值指向的b位字符相等,則該a位的nextval就指向b位的nextval值,如果不等,則該a位的nextval值就是它自己a位的next值。 這應該是最淺顯的解釋了。如字符串"ababaaab"的next數組以及nextval數組分別為:
| 下標 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 子串 | a | b | a | b | a | a | a | b |
| next | -1 | 0 | 0 | 1 | 2 | 3 | 1 | 1 |
| nextval | -1 | 0 | -1 | 0 | -1 | 3 | 1 | 0 |
我們來分析下代碼:
void GetNextval(SqString t,int nextval[])
//由模式串t求出nextval值
{int j=0,k=-1;nextval[0]=-1;while (j<t.length) {if (k==-1 || t.data[j]==t.data[k]) { j++;k++;if (t.data[j]!=t.data[k])
//這里的t.data[k]是t.data[j]處字符不匹配而會回溯到的字符
//為什么?因為沒有這處if判斷的話,此處代碼是next[j]=k;
//next[j]不就是t.data[j]不匹配時應該回溯到的字符位置嘛nextval[j]=k;else nextval[j]=nextval[k];
//這一個代碼含義是不是呼之欲出了?
//此時nextval[j]的值就是就是t.data[j]不匹配時應該回溯到的字符的nextval值
//用較為粗鄙語言表訴:即字符不匹配時回溯兩層后對應的字符下標}else k=nextval[k]; }}
int KMPIndex1(SqString s,SqString t)
//修正的KMP算法
//只是next換成了nextval
{int nextval[MaxSize],i=0,j=0;GetNextval(t,nextval);while (i<s.length && j<t.length) {if (j==-1 || s.data[i]==t.data[j]) { i++;j++; }else j=nextval[j];}if (j>=t.length) return(i-t.length);elsereturn(-1);
}
剩下的話
在寫這篇博客時,我想起了編譯原理老師講過的一些知識,其實KMP算法的步驟與自動機有不少相似之處,有興趣的朋友不妨聯系對比一下。
參考書籍
《數據結構教程》(第5版) 李春葆
《大話數據結構》 程杰
---------------------
作者:哈頓之光
來源:CSDN
原文:https://blog.csdn.net/weixin_46007276/article/details/104372119
版權聲明:本文為作者原創文章,轉載請附上博文鏈接!
內容解析By:CSDN,CNBLOG博客文章一鍵轉載插件

)
![[轉]LVS負載均衡(LVS簡介、三種工作模式、十種調度算法)](http://pic.xiahunao.cn/[轉]LVS負載均衡(LVS簡介、三種工作模式、十種調度算法))





![[轉]Docker超詳細基礎教程,快速入門docker](http://pic.xiahunao.cn/[轉]Docker超詳細基礎教程,快速入門docker)
)
)








