本章通過擴張紅黑樹構造出兩種數據結構:動態順序統計和區間樹。
1、動態順序統計:查找倒數第i小的數據 復雜度為 ?lg(n)
為什么是擴張紅黑樹而不是搜索二叉樹或者二叉樹?
相對于搜索二叉樹,紅黑樹的平衡性更好,高度在lg(n) 。這樣查找時的復雜度就是 lg(n)而不是n。在第9章順序統計量的時候列出了運行時間期望為線性和最壞運行時間為線性的
算法(http://www.cnblogs.com/NeilZhang/p/5650226.html) 。
struct的結點的結構: 與一般的紅黑樹相比,增加了 size ,對于任意一個結點 ?p.size = p.left->size + p.right->size + 1?
struct RBTreeNode {int key;int color;struct RBTreeNode *parent;struct RBTreeNode *left;struct RBTreeNode *right;int size; };
對于檢索具有給定排序的元素:逐層查找
OS_SELECT(x,i)r = size[left[x]]+1; //先計算x的處于的位置if i = r //x正好是第i小的關鍵字then return x;else if i < r //x比第i關鍵字大,則在其左子樹查找then return OS_SELECT(left[x],i)else return OS_SELECT(right[x],i-r) //x比第i關鍵字小,則在其右子樹查找
確定一個元素的秩(知道元素的值大小,確定它的 排序位數)
OS-RANK(T,x)r=x.left.size +1 y=xwhile y!=T.rootif y==y.p.rightr=r+y.p.left.size + 1y=y.p return r
樹的維護
主要是針對 插入 和刪除 操作的維護,在紅黑樹的插入刪除的基礎之上還要 在插入和刪除之后 維護 size的大小,(需要從這個分支一直到root結點)復雜度為 lg(n)
對于紅黑樹的旋轉操作也要在其中添加有關size的比變化。
?
2、如何擴張數據結構
對一種數據結構的擴張過程分為四個步驟:
1)選擇基礎數據結構
2)確定要在基礎數據結構中添加哪些信息
3)驗證可用基礎數據結構上的基本修改操作來維護這些新添加的信息
4)設計新的操作
書中給出了對紅黑樹進行擴張的定理,并給出了證明,這個看的時候有些難度,暫時跳過了。大概意思就是說當紅黑樹被選作基礎數據結構時,某些類型的附加信息總是可以用插入和刪除來進行有效地維護。
?
3、區間樹
這小結講的是擴張紅黑樹以支持由區間構成的動態集合上的操作。區間可以很方便的表示各占用一段連續時間的一些事情。區間樹是一種動態集合進行維護的紅黑樹,該集合中的每個元素x都包含在一個區間int[x]。區間樹支持下列操作:
INTERVAL_INSERT(T,x):將包含區間域int的元素x插入到區間樹T中
INTERVAL_DELETE(T,X):從區間樹T中刪除元素x
INTERVAL_SEARCH(T,i):返回一個指向區間樹T中元素x的指針,使int[x]與i重疊,若集合中無此元素存在,則返回nil[T]。
修改紅黑樹得到的區間樹如下圖所示:
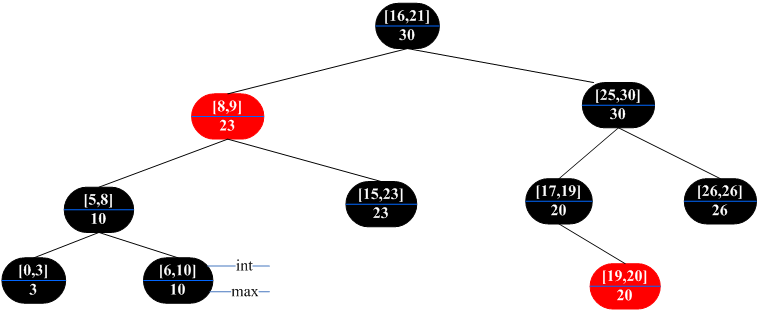
從圖可以看出,對區間樹以每個節點的左端點值進行中序變量即可得到有序的序列。有了區間樹的結果就很容易實現其相關操作。
?



)















