楔子

Plan_Phase(GC的計劃階段)很早就接觸了，但是后面一直沒用到，忘記了，此次又用到了，幾乎忘光了，費了很大力氣理解它，記錄下，以免又忘記了。

主題

計劃階段(plan_phase)主要就兩個部分，一個是堆里面的對象構建一顆龐大的二叉樹。但是，這個二叉樹如果過于龐大，則成了性能瓶頸。于是乎，第二個部分Brick_table出現了，它主要是分割這個龐大的二叉樹，以消弭性能瓶頸問題。

構建不規則二叉樹

構建二叉樹之前，先了解一些概念。當實例化一個對象之后，這個對象存儲在堆里面。堆實際上是一長串的內存地址，不受CPU棧的管控，所以導致了它不能自動釋放，需要手動。在這一長串的地址里面，可以分為固定對象和非固定對象。

1.固定對象概念

首先看下固定句柄，固定句柄就是把托管對象傳遞到費托管對象的堆棧里面去，固定句柄本身在托管里面進行管理，而它包含的對象就叫做固定對象。

至于非固定對象，就是普通的對象了，此處不再贅述。

在進行GC計劃階段的時候，會循環遍歷當前需要收集的垃圾的代（generation）里面包含的所有堆,然后區分出包含固定對象的堆段，和非固定對象的堆段。

區分規則是怎么樣的呢？非常簡單，具體的就是如果相鄰的兩個對象都是非固定對象或者都是固定對象，則把這兩個對象作為一個堆段，繼續查找后面的對象。如果后續的對象跟前面的對象相同，則跟前面的兩個對象放在一起形成一個堆段（如果后面還有相同的，則繼續放在一起），如果不同，則此堆段到此為止。后面繼續以同樣的邏輯遍歷，形成一個個的小堆段（以node表述）。

2.這里有一個特性：

固定堆段（也就是固定對象組成的堆段）的末尾必須跟一個非固定對象（這么做的原因，是避免固定對象的末尾被覆蓋，只覆蓋非固定對象的末尾）。

二叉樹的構建，就建立在這些固定對象堆段和非固定對象堆段上的。這些一個個的堆段作為二叉樹的根節點和葉子結點，構成了二叉樹的本身。

3.相關構建

一：plug_and_pair結構
plug_and_pair存在于上面被分割的堆段的前面，堆段以node(節點)表示，則此結構(plug_and_pair*)node)[-1]的位置

struct plug
{uint8_t *  skew[plug_skew / sizeof(uint8_t *)];
};class pair
{public:short left;short right;
};
struct plug_and_pair
{pair        m_pair;plug        m_plug;
};

pair的left和right成員分別表示當前堆段距離其前一個堆段和后一個堆段的距離長度。

二：構建邏輯
構建邏輯分為三種，數字一般可以分為奇數和偶數。計算機也是一樣，但是除了這兩種之外，偶數里面還可以分裂出另外一種情況，就是一個數字是2的次方數。舉個例子，比如：1,2,3,4,5,6,7,8,9,10。這十個數字里面，明顯的奇數：1,3,5,7,9。偶數：2,4,6,8,10。再分裂下二的次方數：2,4,8。注意看，最后分裂的結果2,4,8分別是2的1次方，2次方和3次方。剔除了6和10這兩個數字。
那么總結下，三種邏輯以上面試個數字舉例分別為：
遍歷循環以上十個數字。
第一種(if(true))：1,2,4,8 if(!(n&(n-1))) n分別為2,4,8。if里為true
第二種(if(true))：3,5,7,9 if(n&1) n分別為1,3,5,7,9。if里為true
第三種(if(true))：6,10 如果以上兩種不成立，則到第三種這里來。

三：構建樹身
如上所述，通過對堆里面的對象進行固定和非固定對象區分，變成一個個的小堆段(node)。這些小堆段從左至右依次編號：1,2,3,4,5,6,7,8,9.......N。然后通過構建邏輯這部分進入到if里面去。

1.(if(true))：

1,2,4,8編號的node會進入這里，主要是設置左節點和tree
set_node_left_child (new_node, (tree - new_node));tree = new_node;

2.(if(true))：

3,5,7,9編號的node會進入這里，主要是設置右節點
set_node_right_child (last_node, (new_node - last_node));

3.(if(true))：

6,10編號的會進入這里，主要是把原來的二叉樹的右子節點變成新的node(new_node)的左子節點，切斷二叉樹與它自己右子節點的聯系。然后把新的node(new_node）,變成原來二叉樹的右子節點。uint8_t*  earlier_node = tree;size_t imax = logcount(sequence_number) - 2;//這里是獲取需要變成的二叉樹的右子樹節點的層級。for (size_t i = 0; i != imax; i++)//如果層級不等于0，則獲取到二叉樹根節點到右子節點的距離，然后把根節點與右子節點相加得到二叉樹右子節點。如此循環遍歷，到二叉樹最底層的右子節點為止。{earlier_node = earlier_node + node_right_child (earlier_node);}獲取到最后一顆二叉樹的根節點的右子樹的距離int tmp_offset = node_right_child (earlier_node);assert (tmp_offset); // should never be empty把最后一顆二叉樹的根節點和最后一顆二叉樹的右子節點相加，設置為新的node(new_node)的左子樹。set_node_left_child (new_node, ((earlier_node + tmp_offset ) - new_node));把最后一顆二叉樹的右子樹節點設置為新的node(new_node)節點，同時也是斷了開與原來右子樹的聯系。set_node_right_child (earlier_node, (new_node - earlier_node));

GC plan_phase的二叉樹構建本身并不復雜，而是復雜的邏輯和詭異的思維方式。

最終的構建的二叉樹形式如下圖所示：

四.分割二叉樹
當以上二叉樹被構建之后，如有幾千個節點（node,小堆段）會形成龐大的一棵樹。所以需要分割功能，用以來保證性能。

當二叉樹包含的小堆段（node）的長度超過2的12次方（4kb），這棵二叉樹就會被分割。

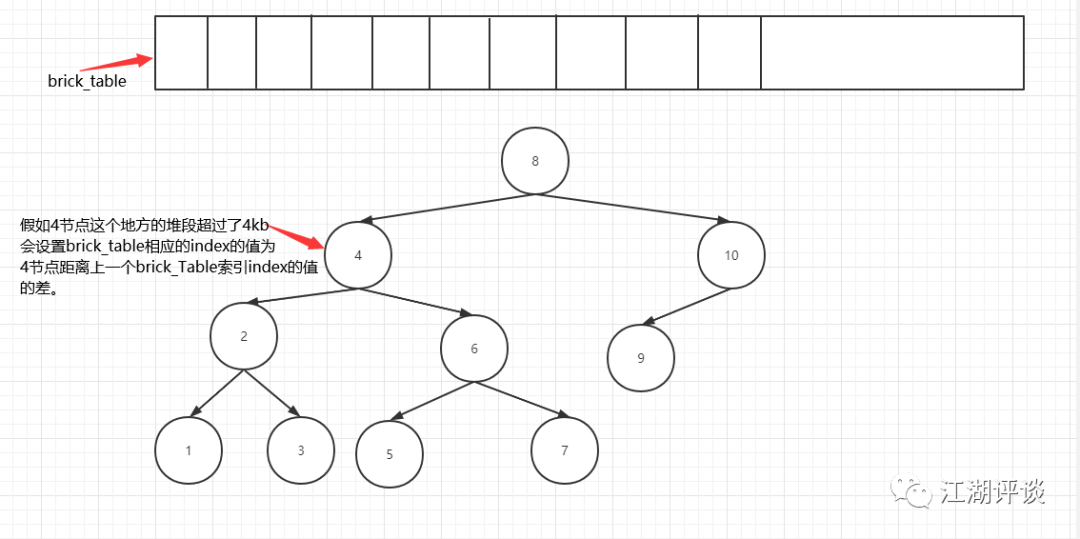
Brick_table里面屬于這個4節點范圍內的都是賦值為-1，表示你要在4節點上尋找你需要的節點。

源碼：

最后上一下源碼
1.構建二叉樹：

uint8_t* gc_heap::insert_node (uint8_t* new_node, size_t sequence_number,uint8_t* tree, uint8_t* last_node)
{dprintf (3, ("IN: %Ix(%Ix), T: %Ix(%Ix), L: %Ix(%Ix) [%Ix]",(size_t)new_node, brick_of(new_node),(size_t)tree, brick_of(tree),(size_t)last_node, brick_of(last_node),sequence_number));if (power_of_two_p (sequence_number)){set_node_left_child (new_node, (tree - new_node));dprintf (3, ("NT: %Ix, LC->%Ix", (size_t)new_node, (tree - new_node)));tree = new_node;}else{if (oddp (sequence_number)){set_node_right_child (last_node, (new_node - last_node));dprintf (3, ("%Ix RC->%Ix", last_node, (new_node - last_node)));}else{uint8_t*  earlier_node = tree;size_t imax = logcount(sequence_number) - 2;for (size_t i = 0; i != imax; i++){earlier_node = earlier_node + node_right_child (earlier_node);}int tmp_offset = node_right_child (earlier_node);assert (tmp_offset); // should never be emptyset_node_left_child (new_node, ((earlier_node + tmp_offset ) - new_node));set_node_right_child (earlier_node, (new_node - earlier_node));dprintf (3, ("%Ix LC->%Ix, %Ix RC->%Ix",new_node, ((earlier_node + tmp_offset ) - new_node),earlier_node, (new_node - earlier_node)));}}return tree;
}

2.切割二叉樹：

size_t gc_heap::update_brick_table (uint8_t* tree, size_t current_brick,uint8_t* x, uint8_t* plug_end)
{dprintf (3, ("tree: %Ix, current b: %Ix, x: %Ix, plug_end: %Ix",tree, current_brick, x, plug_end));if (tree != NULL){dprintf (3, ("b- %Ix->%Ix pointing to tree %Ix",current_brick, (size_t)(tree - brick_address (current_brick)), tree));set_brick (current_brick, (tree - brick_address (current_brick)));//brick_table索引處的值是：根節點tree距離當前current_brick對應的地址的距離}else{dprintf (3, ("b- %Ix->-1", current_brick));set_brick (current_brick, -1);}size_t  b = 1 + current_brick;ptrdiff_t  offset = 0;size_t last_br = brick_of (plug_end-1);//上一個plug節點的末尾current_brick = brick_of (x-1);//當前的plug_startdprintf (3, ("ubt: %Ix->%Ix]->%Ix]", b, last_br, current_brick));while (b <= current_brick){if (b <= last_br){set_brick (b, --offset);}else{set_brick (b,-1);}b++;}return brick_of (x);
}

以上參考：
https://github.com/dotnet/coreclr/blob/main/src/gc/gc.cpp