全向輪底盤上安裝兩條磁傳感器帶用于磁導軌尋跡
如簡圖所示，兩條與Y直線相交的黑色線條我們認為是兩條磁檢測傳感器帶
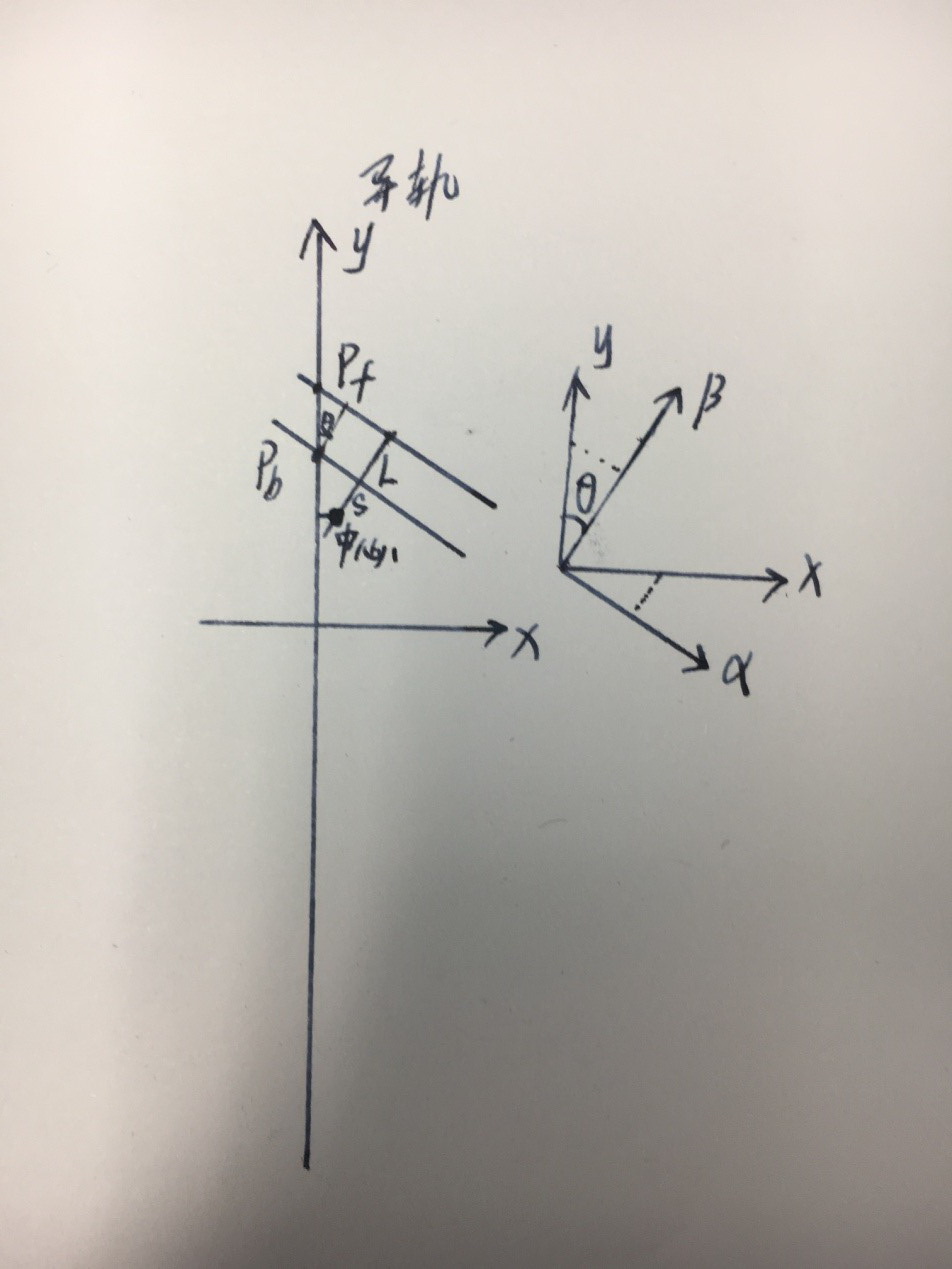
矢量方法修正車體位置
定義軌道左為負向，軌道右為正向。傳感器左檢測為負，右檢測為正；
定義底盤坐標系為αβ，軌道坐標系為XY，車體與軌道坐標系的偏轉角度為θ；
設前傳感器檢測為值為Pf，后傳感器檢測位置為Pb，兩傳感器距離為L，后傳感器與機器人中心點的距離為S（如中心在兩傳感器中間，S符號為負，如中心在后傳感器后面，S符號為正）。中心點旋轉偏角為θ，橫向偏移為Poff。
由幾何關系可得出θ = tan-1((Pb-Pf)/L)
Poff??= (-Pb/tanθ-S)sinθ?
然后通過轉換關系（諸如PID，模糊等方式）將θ 轉換為對應的底盤自旋速度Vθ?（注意正反轉符號），Poff 轉換為對應的磁導軌X軸速度矢量Voff? （注意Voff 帶有方向），再分解為建立到車體上的αβ速度坐標系Voff?sinθ 、Voff cosθ 。
此外底盤還有沿磁導軌Y軸方向的運動速度V，該速度同樣由建立到車體上的αβ速度坐標系合成，V?sinθ 、V?cosθ
則傳遞到電機速度解算函數的速度參數
Vβ?= -Voff?sinθ + V?cosθ
Vα = -Voff?cosθ - V?sinθ
Vω = Vθ?
上面的分析只考慮了底盤實際位置的橫移與旋轉，沒有考慮當前畸變的速度方向的影響，對于車體沿導軌的主速度采用了直接修正的方式去處理，這里忽略了一個情況，速度不是瞬變的，車體受慣性仍會沿當前主速度方向運動，這樣即使修正了主速度矢量與導軌Y方向對齊，但原來偏離了θ'角度的主速度仍會影響車體運動。一般來說θ'會在0到θ之間，要具體求出需要獲取當前各個輪子的速度，然后通過坐標換算反求。為了抵消這個原主速度的影響并簡化計算，我們可以在Voff上再疊加一個修正速度，這個速度受上一個主速度大小和θ影響。
這樣新的Voffsum =Voff?+kVlastsinθ
k為修正系數
這樣修正上面的傳遞到電機速度解算函數的速度參數
Vβ?= -Voffsum?sinθ + V?cosθ
Vα?= -Voffsum?cosθ - V?sinθ
Vω?= Vθ?
?
)
)
)
