tarjan算法詳解

https://blog.csdn.net/jeryjeryjery/article/details/52829142?locationNum=4&fps=1

以防鏈接失效，特此轉載此博，如有侵權請見諒

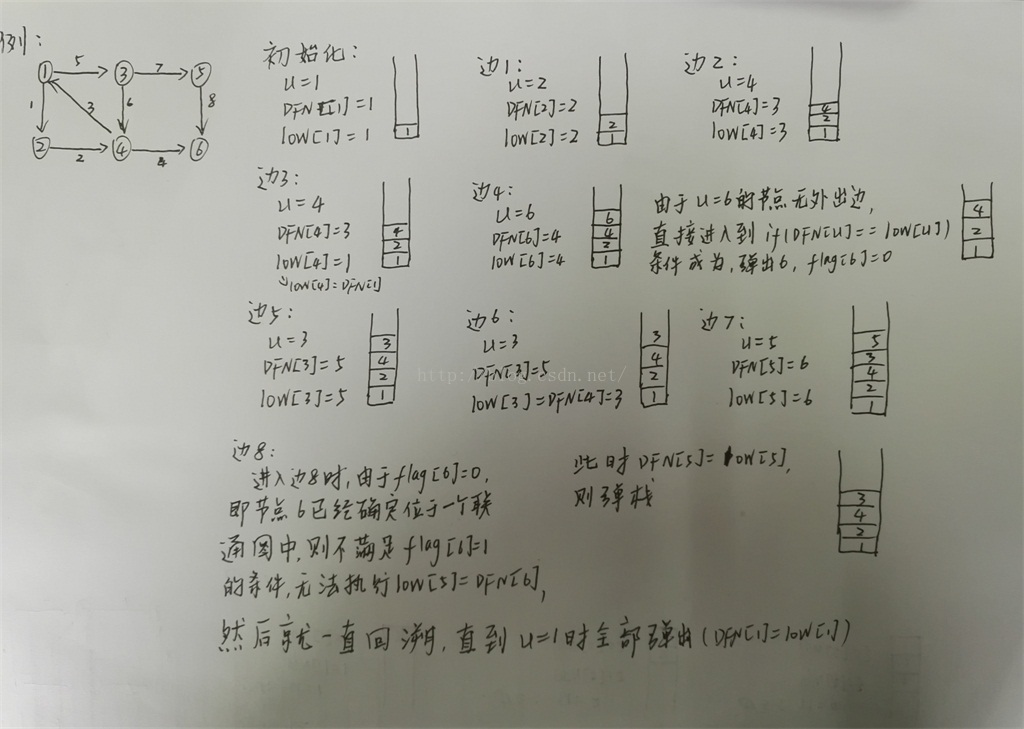
?在有向圖G中，如果兩個頂點間至少存在一條路徑，稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通，稱G是一個強連通圖。非強連通圖有向圖的極大強連通子圖，稱為強連通分量(strongly connected components)。如下圖中，強連通分量有：{1,2,3,4}，{5}，{6}

? ? ? ?Tarjan算法是基于對圖深度優先搜索的算法，每個強連通分量為搜索樹中的一棵子樹。搜索時，把當前搜索樹中未處理的節點加入一個堆棧，回溯時可以判斷棧頂到棧中的節點是否為一個強連通分量。Tarjan算法有點類似于基于后序的深度遍歷搜索和并查集的組合，充分利用回溯來解決問題。
在Tarjan算法中為每個節點i維護了以下幾個變量：
DFN[i]：深度優先搜索遍歷時節點i被搜索的次序。
low[i]：節點i能夠回溯到的最早位于棧中的節點。
flag[i]：標記幾點i是否在棧中。

Tarjan算法的運行過程：
（1）.首先就是按照深度優先搜索算法搜索的次序對圖中所有的節點進行搜索。
（2）.在搜索過程中，對于任意節點u和與其相連的節點v，根據節點v是否在棧中來進行不同的操作：
*節點v不在棧中，即節點v還沒有被訪問過，則繼續對v進行深度搜索。
*節點v已經在棧中，即已經被訪問過，則判斷節點v的DFN值和節點u的low值的大小來更新節點u的low值。如果節點v的?DFN值要小于節點u的low值，根據low值的定義（能夠回溯到的最早的已經在棧中的節點），我們需要用DFN值來更新u?的low值。
（3）.在回溯過程中，對于任意節點u用其子節點v(其實不能算是子節點，只是在深度遍歷的過程中，v是在u之后緊挨著u的節點)的? ?low值來更新節點u的low值。因為節點v能夠回溯到的已經在棧中的節點，節點u也一定能夠回溯到。因為存在從u到v的直接路徑，所以v能夠到的節點u也一定能夠到。

（4）.對于一個連通圖，我們很容易想到，在該連通圖中有且僅有一個節點u的DFN值和low值相等。該節點一定是在深度遍歷的過程中，該連通圖中第一個被訪問過的節點，因為它的DFN值和low值最小，不會被該連通圖中的其他節點所影響。

? ? ? 下面我們證明為什么僅有一個節點的DFN和low值相等。假設有兩個節點的DFN值和low值相等，由于這兩個節點的DFN值一定不相同?（DFN值的定義就是深度遍歷時被訪問的先后次序），所以兩個的low值也絕對不相等。由于位于同一個連通圖中，所以兩個節點必定相互可達，那么兩者的low值一定會被另外一個所影響（要看誰的low值更小），所以不可能存在兩對DFN值和low值相等的節點。

? ? ? ?所以我們在回溯的過程中就能夠通過判斷節點的low值和DFN值是否相等來判斷是否已經找到一個子連通圖。由于該連通圖中的DFN值和low值相等的節點是該連通圖中第一個被訪問到的節點，又根據棧的特性(先壓入? 棧的節點在棧的更里面)，則該節點在最里面。所以能夠通過不停的彈棧，直到彈出該DFN值和low值相同的節點來彈出該連通圖中所有的節點。

Tarjan算法的C++實現代碼如下，可以配合上面的圖加以理解：

[cpp]?view plaincopy

1. #include<iostream>??
2. using?namespace?std;??
3. int?DFN[105];??????????????????????????????????//記錄在做dfs時節點的搜索次序??
4. int?low[105];??????????????????????????????????//記錄節點能夠找到的最先訪問的祖先的記號??
5. int?count=1;???????????????????????????????????//標記訪問次序，時間戳??
6. int?stack[105];????????????????????????????????//壓入棧中??
7. int?top=-1;??
8. int?flag[105];?????????????????????????????????//標記節點是否已經在棧中??
9. int?number=0;??
10. int?j;??
11. int?matrix[105][105]={{0,1,1,0,0,0},{0,0,0,1,0,0},{0,0,0,1,1,0},{1,0,0,0,0,1},{0,0,0,0,0,1},{0,0,0,0,0,0}};??
12. int?length;????????????????????????????????????//圖的長度??
13. void?tarjan(int?u){??
14. ????DFN[u]=low[u]=count++;?????????????????????//初始化兩個值，自己為能找到的最先訪問的祖先??
15. ????stack[++top]=u;??
16. ????flag[u]=1;?????????????????????????????????//標記為已經在棧中??
17. ??
18. ????for(int?v=0;v<length;v++){??
19. ????if(matrix[u][v]){??
20. ????????if(!DFN[v]){???????????????????????//如果點i沒有被訪問過??
21. ????????tarjan(v);?????????????????????//遞歸訪問??
22. ????????if(low[v]<low[u])??
23. ????????????low[u]=low[v];?????????????//更新能找的到祖先??
24. ????????}??
25. ????????else{??????????????????????????????//如果訪問過了，并且該點的DFN更小，則??
26. ????????if(DFN[v]<low[u]&&flag[v])?????//flag[v]這個判斷條件很重要，這樣可以避免已經確定在其他聯通圖的v,因為u到v的單向邊而影響到u的low??
27. ????????low[u]=DFN[v];?????????????????//也就是已經確定了的聯通圖要剔除掉，剔除的辦法就是判斷其還在棧中，因為已經確定了的連通圖的點??
28. ????????}??????????????????????????????????//flag在下面的do?while中已經設為0了(即已經從棧中剔除了)??
29. ????}??
30. ????}??
31. ??
32. ????//往后回溯的時候，如果發現DFN和low相同的節點，就可以把這個節點之后的節點全部彈棧，構成連通圖??
33. ????if(DFN[u]==low[u]){??
34. ????number++;???????????????????????????????//記錄連通圖的數量??
35. ????do{??
36. ????????j=stack[top--];?????????????????????//依次取出，直到u??
37. ????????cout<<j<<"?";??
38. ????????flag[j]=0;??????????????????????????//設置為不在棧中??
39. ????}while(j!=u);??
40. ????????cout<<endl;??
41. ????}??
42. }??
43. int?main(){??
44. ??????
45. ????memset(DFN,0,sizeof(DFN));??????????????????//數據的初始化??
46. ????memset(low,0,sizeof(low));??
47. ????memset(flag,0,sizeof(flag));??
48. ??????
49. ????length=6;??
50. ????tarjan(0);??
51. ??
52. ????cout<<endl;??
53. ????for(int?i=0;i<6;i++){??
54. ????cout<<"DFN["<<i<<"]:"<<DFN[i]<<"?low["<<i<<"]:"<<low[i]<<endl;??
55. ????}??
56. ????return?0;??
57. } ?

轉載于:https://www.cnblogs.com/cglongge/p/8722202.html

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/280702.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/280702.shtml
英文地址，請注明出處：http://en.pswp.cn/news/280702.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！