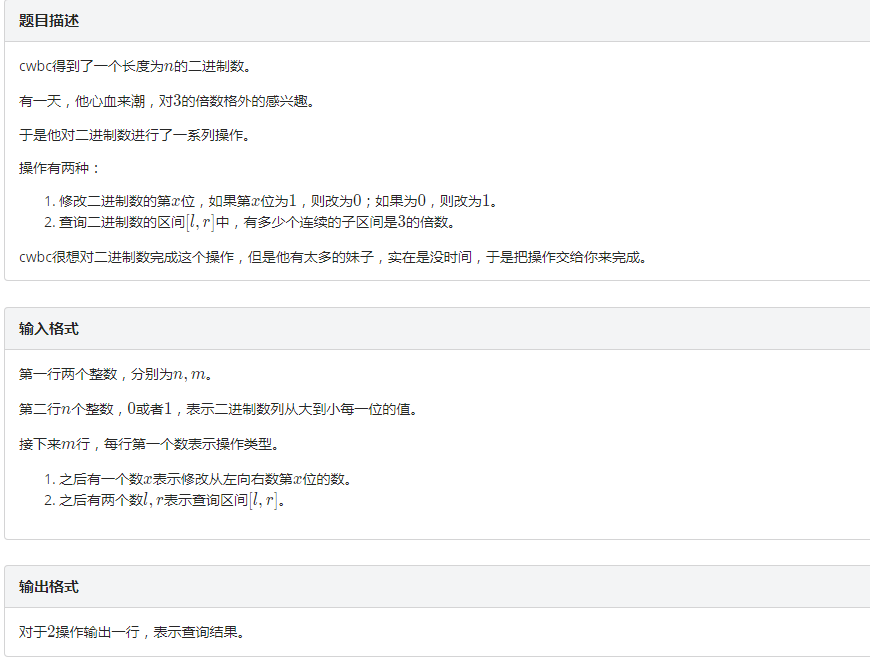
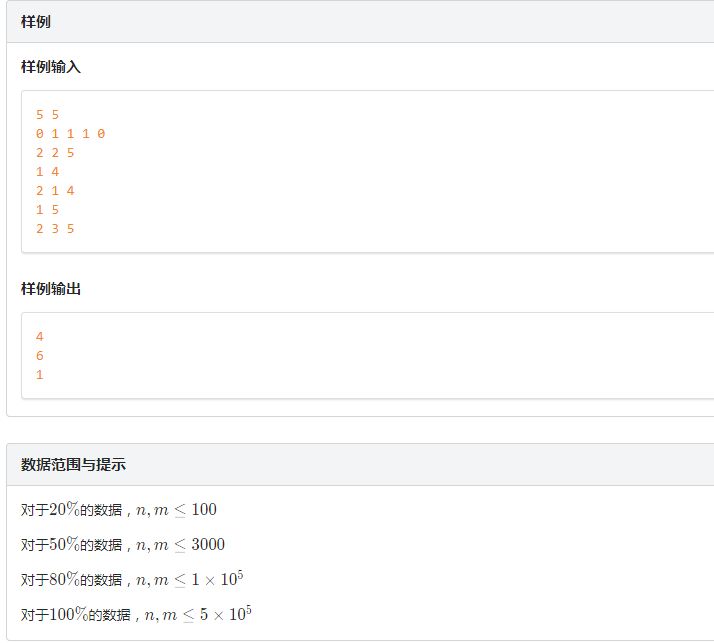
?
? ? 發現一個區間[L,R]代表的2進制數是3的倍數,當且僅當從L開始的后綴二進制值 - 從R+1開始的后綴二進制值 是 3 的倍數 (具體證明因為太簡單而被屏蔽)。
? ? 于是我們就可以在每個點維護從它開始的后綴二進制數的值,因為在%3同余系下只有3個數,所以我們可以很容易的用線段樹進行區間維護,然后答案就是 C(num[0],2) + C(num[1],2) + C(num[2],2)? ? [注意如果查詢區間是 [l,r]的話那么 在線段樹中查找的區間是 [l,r+1] ,因為區間[x,y]對應 x和y+1后綴相減]。
? ? 但是有修改咋辦呢?
? ? 給每個位置設一個權值,后綴長度是奇數的權值是1,反之則是2。
? ? 然后稍微動腦子想一下,如果? 一個位置修改前是 1? 和? 這個位置權值是 1? 這兩個條件只滿足其中一個,那么就是對前綴區間 +1;否則就是對前綴區間+2。
? ? 所以隨便寫個線段樹打打標記就好啦。
?
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=500005;
int a[maxn],val[maxn],tag[maxn*4];
int n,m,sum[maxn*4][3],hz[maxn];
int le,ri,W,opt,ans[3];inline int read(){int x=0; char ch=getchar();for(;!isdigit(ch);ch=getchar());for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';return x;
}inline int add(int x,int y){ x+=y; return x>=3?x-3:x;}inline void maintain(int o,int lc,int rc){sum[o][0]=sum[lc][0]+sum[rc][0];sum[o][1]=sum[lc][1]+sum[rc][1];sum[o][2]=sum[lc][2]+sum[rc][2];
}inline void CG(int o,int VAL){int T=sum[o][0];tag[o]=add(tag[o],VAL);if(VAL==1){sum[o][0]=sum[o][2];sum[o][2]=sum[o][1];sum[o][1]=T;}else{sum[o][0]=sum[o][1];sum[o][1]=sum[o][2];sum[o][2]=T;}
}inline void pushdown(int o,int lc,int rc){if(tag[o]){CG(lc,tag[o]),CG(rc,tag[o]);tag[o]=0;}
}void build(int o,int l,int r){if(l==r){sum[o][hz[l]]++;return;}int mid=l+r>>1,lc=o<<1,rc=(o<<1)|1;build(lc,l,mid),build(rc,mid+1,r);maintain(o,lc,rc);
}void update(int o,int l,int r){if(l>=le&&r<=ri){CG(o,W);return;}int mid=l+r>>1,lc=o<<1,rc=(o<<1)|1;pushdown(o,lc,rc);if(le<=mid) update(lc,l,mid);if(ri>mid) update(rc,mid+1,r);maintain(o,lc,rc);
}void query(int o,int l,int r){if(l>=le&&r<=ri){ans[0]+=sum[o][0];ans[1]+=sum[o][1];ans[2]+=sum[o][2];return;}int mid=l+r>>1,lc=o<<1,rc=(o<<1)|1;pushdown(o,lc,rc);if(le<=mid) query(lc,l,mid);if(ri>mid) query(rc,mid+1,r);
}inline ll getC(int x){ return x?x*(ll)(x-1)>>1:0;}inline void solve(){while(m--){opt=read();if(opt==1){le=1,ri=read();if(a[ri]+val[ri]==2) W=2; else W=1;a[ri]^=1,update(1,1,n);}else{le=read(),ri=read(),ri++;ans[0]=ans[1]=ans[2]=0;query(1,1,n);printf("%lld\n",getC(ans[0])+getC(ans[1])+getC(ans[2]));}}
}int main(){n=read(),m=read();for(int i=1;i<=n;i++) a[i]=read();n++,val[n]=2,hz[n]=0;for(int i=n-1;i;i--){val[i]=3-val[i+1];hz[i]=add(hz[i+1],val[i]*a[i]);}build(1,1,n);solve();return 0;
}









)




)




