線性回歸是一種回歸分析技術，回歸分析本質上就是一個函數估計的問題（函數估計包括參數估計和非參數估計），就是找出因變量和自變量之間的因果關系。回歸分析的因變量是應該是連續變量，若因變量為離散變量，則問題轉化為分類問題，回歸分析是一個有監督學習問題。
線性其實就是一系列一次特征的線性組合，在二維空間中是一條直線，在三維空間中是一個平面，然后推廣到n維空間，可以理解維廣義線性吧。
例如對房屋的價格預測，首先提取特征，特征的選取會影響模型的精度，比如房屋的高度與房屋的面積，毫無疑問面積是影響房價的重要因素，二高度基本與房價不相關
下圖中挑選了 面積、我是數量、層數、建成時間四個特征，然后選取了一些train Set{x(i)?, y(i)}。
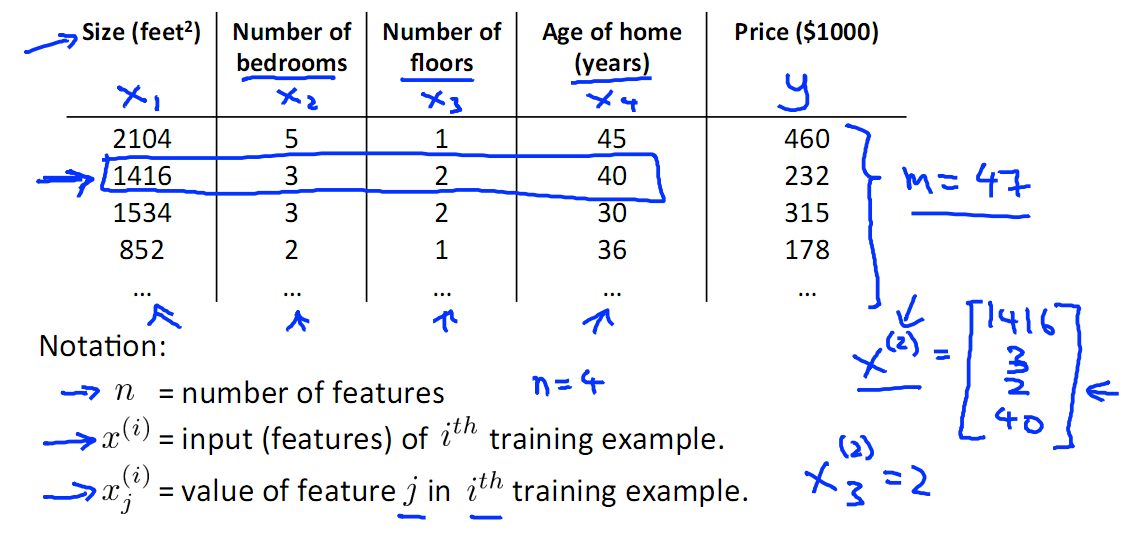
?有了這些數據之后就是進行訓練，下面附一張有監督學習的示意圖
Train Set 根據 學習算法得到模型h，對New Data x，直接用模型即可得到預測值y，本例中即可得到房屋大小，其實本質上就是根據歷史數據來發現規律，事情總是偏向于向歷史發生過次數多的方向發展。
下面就是計算模型了，才去的措施是經驗風險最小化，即我們訓練模型的宗旨是，模型訓練數據上產生結果
,?要與實際的y(i)越接近越好（假定x0?=1），定義損失函數J(θ)如下,即我們需要損失函數越小越好，本方法定義的J(θ)在最優化理論中稱為凸（Convex）函數，即全局只有一個最優解，然后通過梯度下降算法找到最優解即可，梯度下降的形式已經給出。
?
?
梯度下降的具體形式：關于梯度下降的細節，請參閱?梯度下降詳解
局部加權回歸
有時候樣本的波動很明顯，可以采用局部加權回歸，如下圖，紅色的線為局部加權回歸的結果，藍色的線為普通的多項式回歸的結果。藍色的線有一些欠擬合了。
局部加權回歸的方法如下，首先看線性或多項式回歸的損失函數“
很明顯，局部加權回歸在每一次預測新樣本時都會重新確定參數，以達到更好的預測效果。當數據規模比較大的時候計算量很大，學習效率很低。并且局部加權回歸也不是一定就是避免underfitting，因為那些波動的樣本可能是異常值或者數據噪聲。
?
在求解線性回歸的模型時，有兩個需要注意的問題
一就是特征組合問題，比如房子的長和寬作為兩個特征參與模型的構造，不如把其相乘得到面積然后作為一個特征來進行求解，這樣在特征選擇上就做了減少維度的工作。
二就是特征歸一化（Feature Scaling），這也是許多機器學習模型都需要注意的問題。
有些模型在各個維度進行不均勻伸縮后，最優解與原來等價，例如logistic regression。對于這樣的模型，是否標準化理論上不會改變最優解。但是，由于實際求解往往使用迭代算法，如果目標函數的形狀太“扁”，迭代算法可能收斂得很慢甚至不收斂。所以對于具有伸縮不變性的模型，最好也進行數據標準化。
歸一化后有兩個好處：
1. 提升模型的收斂速度
如下圖，x1的取值為0-2000，而x2的取值為1-5，假如只有這兩個特征，對其進行優化時，會得到一個窄長的橢圓形，導致在梯度下降時，梯度的方向為垂直等高線的方向而走之字形路線，這樣會使迭代很慢，相比之下，右圖的迭代就會很快
?
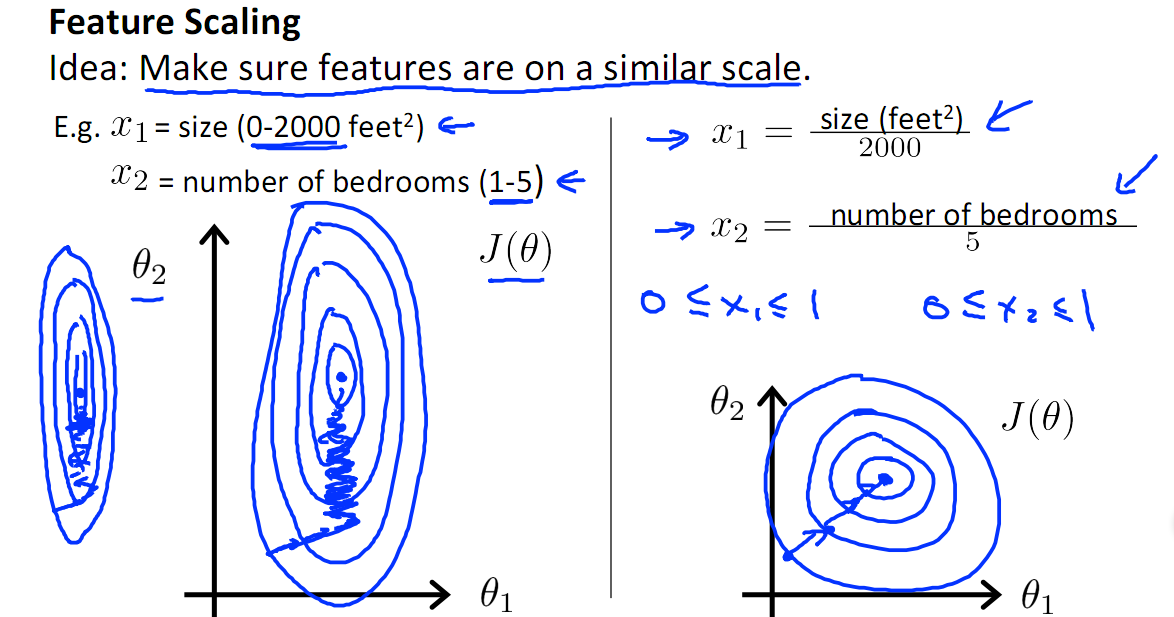
2.提升模型的精度
歸一化的另一好處是提高精度，這在涉及到一些距離計算的算法時效果顯著，比如算法要計算歐氏距離，上圖中x2的取值范圍比較小，涉及到距離計算時其對結果的影響遠比x1帶來的小，所以這就會造成精度的損失。所以歸一化很有必要，他可以讓各個特征對結果做出的貢獻相同。
下邊是常用歸一化方法
1）. 線性歸一化，線性歸一化會把輸入數據都轉換到[0 1]的范圍，公式如下
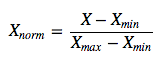
該方法實現對原始數據的等比例縮放，其中Xnorm為歸一化后的數據，X為原始數據，Xmax、Xmin分別為原始數據集的最大值和最小值。
2）.?0均值標準化，0均值歸一化方法將原始數據集歸一化為均值為0、方差1的數據集，歸一化公式如下：
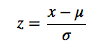
其中，μ、σ分別為原始數據集的均值和方法。該種歸一化方式要求原始數據的分布可以近似為高斯分布，否則歸一化的效果會變得很糟糕。
關于歸一化方法的選擇
1） 在分類、聚類算法中，需要使用距離來度量相似性的時候、或者使用PCA技術進行降維的時候，第二種方法(Z-score standardization)表現更好。
2） 在不涉及距離度量、協方差計算、數據不符合正太分布的時候，可以使用第一種方法或其他歸一化方法。比如圖像處理中，將RGB圖像轉換為灰度圖像后將其值限定在[0 255]的范圍。
選擇方法是參考自http://blog.csdn.net/zbc1090549839/article/details/44103801，至于為什么，我現在也還不清楚
線性回歸，我用java實現的，源碼地址?https://github.com/ooon/toylib
?
參考文獻：
http://www.cnblogs.com/LBSer/p/4440590.html
