用三角函數表示周期函數
傅里葉的相關理論始于下面假設:對于周期為1的信號$f(t)$,可以由不同頻率的三角函數組成,
$f(t) = \frac{a_0}{2}+\displaystyle{\sum^{\infty}_{k=1}}(a_kcos(2\pi kt)+b_ksin(2\pi kt))$
組成的基礎波形為一個信號對,分別為$cos(2\pi t)$以及$sin(2\pi t)$,波形的頻率覆蓋范圍為$k=1,2,3,\cdots$(角頻率為$2\pi k$),在這些頻率上的系數(即振幅)對為$(a_1,b_1),(a_2,b_2),(a_3,b_3),\cdots$。
?
?
傅里葉級數
上面的式子可以進一步推導成傅里葉級數形式:
$f(t) = \displaystyle{\sum^{\infty}_{k=-\infty}C_ke^{2\pi ikt} }$
從這個表現形式看出,組成的基礎波形為$e^{2\pi it}$,波形的頻率覆蓋范圍是$k=0,\pm 1,\pm 2,\pm 3,\cdots$(角頻率為$2\pi k$),在這些頻率上的系數為$C_0, C_{\pm 1}, C_{\pm 2}, C_{\pm 3}, \cdots$,這些系數由下面的式子得到:
$C_k = \displaystyle{\int_{0}^{1}f(t)e^{-2\pi ikt}dt}$
如果我們把記錄信號在時間上的值的函數$f(t)$稱作該信號在時域上的表現的話,那么該信號在頻率$k$上的系數$C_k$就是該信號在頻域上的表現。傅里葉系數的物理意義就是信號在對應頻率上的振幅。
?
?
傅里葉變換
為了把傅里葉的理論應用到一般信號,我們把周期擴展到$T\to\infty$,那么信號$f(t)$的傅里葉級數變成:
$f(t) = \displaystyle{\lim_{T\to\infty}\sum_{k=-\infty}^{\infty}C_ke^{2\pi i\frac{k}{T}t} }$
此時的傅里葉系數變成:
$C_k = \displaystyle{\lim_{T\to\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-2\pi i\frac{k}{T}t}dt }$
可以看到由于信號$f(t)$在$(-\infty,\infty)$上是可積的,當$T$被擴展到無窮的時候傅里葉系數$C_k$被稀釋成$0$了,因此可以認為一般信號在各個頻率上的傅里葉系數(振幅)為$0$。這種結果對于我們進行傅里葉分析是沒有用處的,因此有了如下傅里葉變換:
令
$\displaystyle{\mathcal{F} f(s) =C_k \times T = \int_{-\infty}^{\infty}e^{-2\pi i st}f(t)dt }$
其中$s = \frac{k}{T}$,即原本是離散的頻率$k$被擴展成了覆蓋$(-\infty,\infty)$的連續變量$s$,因此可以得到
$f(t) = \displaystyle{\int_{-\infty}^{\infty}\mathcal{F} f(s)e^{2\pi ist}ds }$
其中$ds = \frac{1}{T}$,$s$是可以覆蓋所有頻率的變量。
$\displaystyle{\mathcal{F} f(s) }$就是信號$f(t)$的傅里葉變換。但此時傅里葉變換不再具有傅里葉系數的物理意義。
?
?
傅里葉變換的物理意義
Plancherel's Formula
Plancherel's Formula有如下定義:
$\displaystyle{\int_{-\infty}^{\infty}f(t)\overline{g(t)}\,dt=\int_{-\infty}^{\infty}F(s)\overline{G(s)}\,ds}$
證明:
$\begin{align*}\int_{-\infty}^{\infty}f(t)\overline{g(t)}\,dt
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}F(s)e^{2\pi ist}\,ds \right )\overline{\left(\int_{-\infty}^{\infty}G(s')e^{2\pi is't}\,ds' \right )}\,dt \\
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}F(s)e^{2\pi ist}\,ds \right )\left(\int_{-\infty}^{\infty}\overline{G(s')}e^{-2\pi is't}\,ds' \right )\,dt \\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(s)\overline{G(s')}\int_{-\infty}^{\infty}e^{2\pi i(s-s')t}\,dt\,ds'\,ds \\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(s)\overline{G(s')}\delta(s'-s)\,ds'\,ds\qquad \mathcal{F}e^{2\pi ist} = \delta(s'-s)\ ,variable\ is\ s'\\
&=\int_{-\infty}^{\infty}F(s)\int_{-\infty}^{\infty}\overline{G(s')}\delta(s'-s)\,ds'\,\,ds \\
&=\int_{-\infty}^{\infty}F(s)\,\overline{G(s)}\,ds \qquad \delta\ shift\ theorem\\
\end{align*}$
?
Energy Spectral Density
根據Plancherel's Formula,可以得到
$\begin{align*}
\int_{-\infty}^{\infty}|f(t)|^2\,dt
&=\int_{-\infty}^{\infty}f(t)\overline{f(t)}\,dt\\
&=\int_{-\infty}^{\infty}F(s)\overline{F(s)}\,ds\\
&=\int_{-\infty}^{\infty}|F(s)|^2\,ds
\end{align*}$
假設有一個物理實驗,目的是測量電流通過某個電阻時所產生的能量,已知電阻兩端的電勢差會隨著時間變化,為$V(t)$,電阻的阻抗為$R$,那么所產生的能量為:
$\displaystyle{\int_{-\infty}^{\infty}\frac{V(t)^2}{R}dt}$
此時回顧上面所得到的式子
$\displaystyle{\int_{-\infty}^{\infty}|f(t)|^2\,dt=\int_{-\infty}^{\infty}|F(s)|^2\,ds}$
首先是等號左邊:其中信號$f(t)$可以認為是電勢差隨著時間的變化,如果我們忽略電阻抗后,可以認為產生的能量為$\displaystyle{\int_{-\infty}^{\infty}|f(t)|^2\,dt}$。等號右邊的$s$,按照我們前面的討論,$s$代表的就是頻率,因此$|F(s)|^2$可以看作信號的能量在頻域上的能量密度函數(Energy Spectral Density)。如下圖,寬度為$ds$的頻率所蘊含的能量大小為$|F(s)|^2ds$
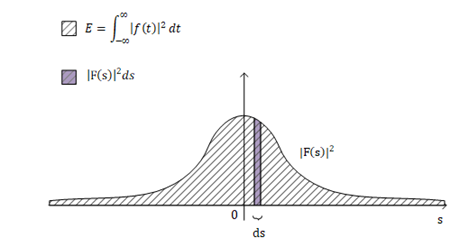
如果我們對信號進行帶通濾波,那么被過濾掉的頻率就無法再繼續貢獻能量,ESD上就會缺少被過濾掉的頻率所對應的區域,相應地傅里葉變換也會缺少被過濾掉的頻率所對應的區域。







)


)








