Sometimes you may need a quick and easy way to access Internet Explorer’s cache. Today we take a look at IECacheView which is a great application to get the job done.

有時，您可能需要一種快速簡便的方法來訪問Internet Explorer的緩存。 今天，我們來看一下IECacheView，它是完成工作的絕佳應用程序。

Setup

建立

There is no installation for you to worry about. Simply unzip the program zip file, place the two files inside (IECacheView.exe and IECacheView.chm) in their own folder in Program Files, and create a shortcut. Everything will be all ready to go.

沒有安裝讓您擔心。 只需解壓縮程序zip文件，然后將兩個文件(IECacheView.exe和IECacheView.chm)放在“程序文件”中其各自的文件夾中，然后創建快捷方式。 一切都準備就緒。

Once you open IECacheView, this is what it will look like…

一旦打開IECacheView，它的外觀將是…

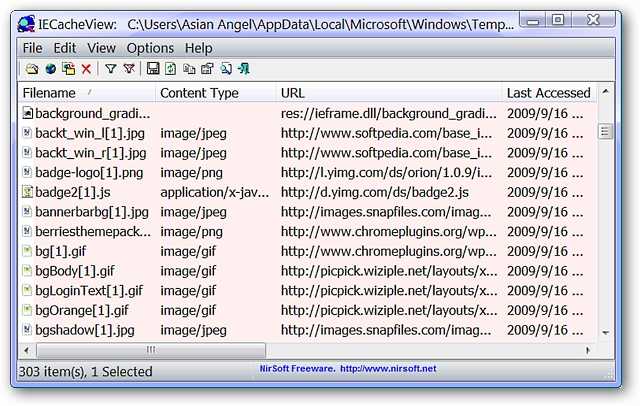
Scroll over to the right of the app and you get additional information and it’s easy to customize what columns are displayed based on your personal needs.

滾動到應用程序的右側，您將獲得更多信息，并且可以輕松地根據您的個人需求自定義顯示哪些列。

Menus

選單

Time for a look at the menu system for IECacheView…here you can see the “File, Edit, & View Menus”. Each one provides a multitude of options that you can apply to folders, the cache, sub-folders, URL opening, saving, deleting, & copying, display (i.e. grid lines and columns), html reports, and more (very nice!).

是時候來看一下IECacheView的菜單系統了……在這里您可以看到“文件，編輯和查看菜單”。 每個選項都提供許多選項，您可以將它們應用于文件夾，緩存，子文件夾，URL打開，保存，刪除和復制，顯示(即網格線和列)，html報告等等(非常好！ ) 。

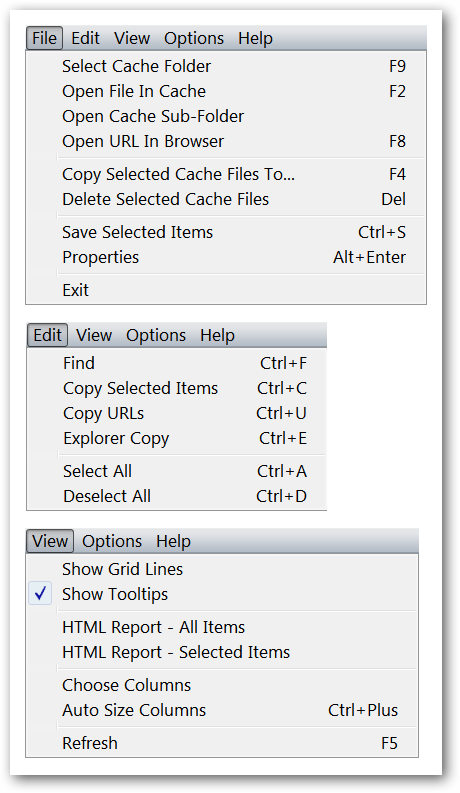
The “Options and Help Menus”. Notice that you can specify the types of files that you would like to have displayed (very convenient!).

“選項和幫助菜單”。 請注意，您可以指定要顯示的文件類型(非常方便！ )。

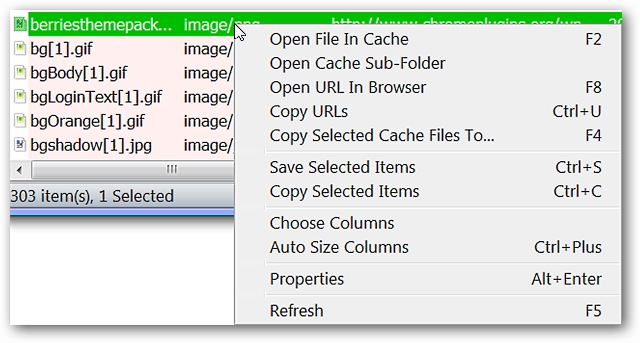
These are the options available in the “Right Click Menu”.

這些是“右鍵菜單”中可用的選項。

Conclusion

結論

IECacheView makes a nice little utility to have around if you ever need a quick and easy way to dig into Internet Explorer’s cache.

如果您需要一種快速簡便的方法來挖掘Internet Explorer的緩存，IECacheView會提供一個不錯的小實用程序。

Links

鏈接

Download IECacheView (version 1.31)

下載IECacheView(1.31版)

Note: Download link is at the bottom of the page.

注意：下載鏈接位于頁面底部。

Works On: Windows 98 – Vista, Internet Explorer 6 – 8

適用于： Windows 98 – Vista，Internet Explorer 6 – 8

Installed On: Windows Vista (32 bit), Service Pack 2

安裝于： Windows Vista(32位)，Service Pack 2

翻譯自: https://www.howtogeek.com/howto/4592/view-internet-explorer-cache-files-the-easy-way/