堆排序

目錄

• 一、定義
• 二、算法分析
• 三、代碼地址

一、定義

1.1 堆

? 此處的堆，指數據結構中的堆。而不是內存中的那種內存堆，內存堆是基于數據結構的一種實現。堆的數據結構是一棵完全二叉樹，它有如下特點：（具體參考下文鏈接）

• 堆是一棵完全二叉樹
• 它總是最小值在根節點（或最大值在根節點）
• 它上一層比下一層小（大）
• 必定有快速刪除根節點，并返回根節點元素的方法
• 在刪除根節點（最小元或者最大元）之后，自動調節使之依然保持堆結構。
• 插入節點依然保持堆結構

? 綜上，堆結構的基本操作是插入和刪除根節點，在操作過程中還會保持堆結構不會被破壞。所以我們可以用堆排序，我們可以通過刪除根節點得到最小值，再刪除根節點，得到第二小值，如此類推，只要一直取根節點，就能得到從小到大的序列。

堆的數據結構：https://www.cnblogs.com/dhcao/p/10591282.html

1.2 堆排序

? 對一個含有N個元素的數組a，我們利用堆排序的做法：

• 首先建立一個二叉堆（最小元在根節點）。根據二叉堆的特性，此過程運行時間\(O(N)\)。
• 然后執行\(N\)次刪除最小元（deleteMin）操作，按照順序，最小的元素先離開堆。
• 將這些元素記錄到第二個數組中，得到一個排序之后的數組（可避免使用第二個數組）。
• 再將這些數組拷貝回來，得到\(N\)個元素的排序。

? 圖解：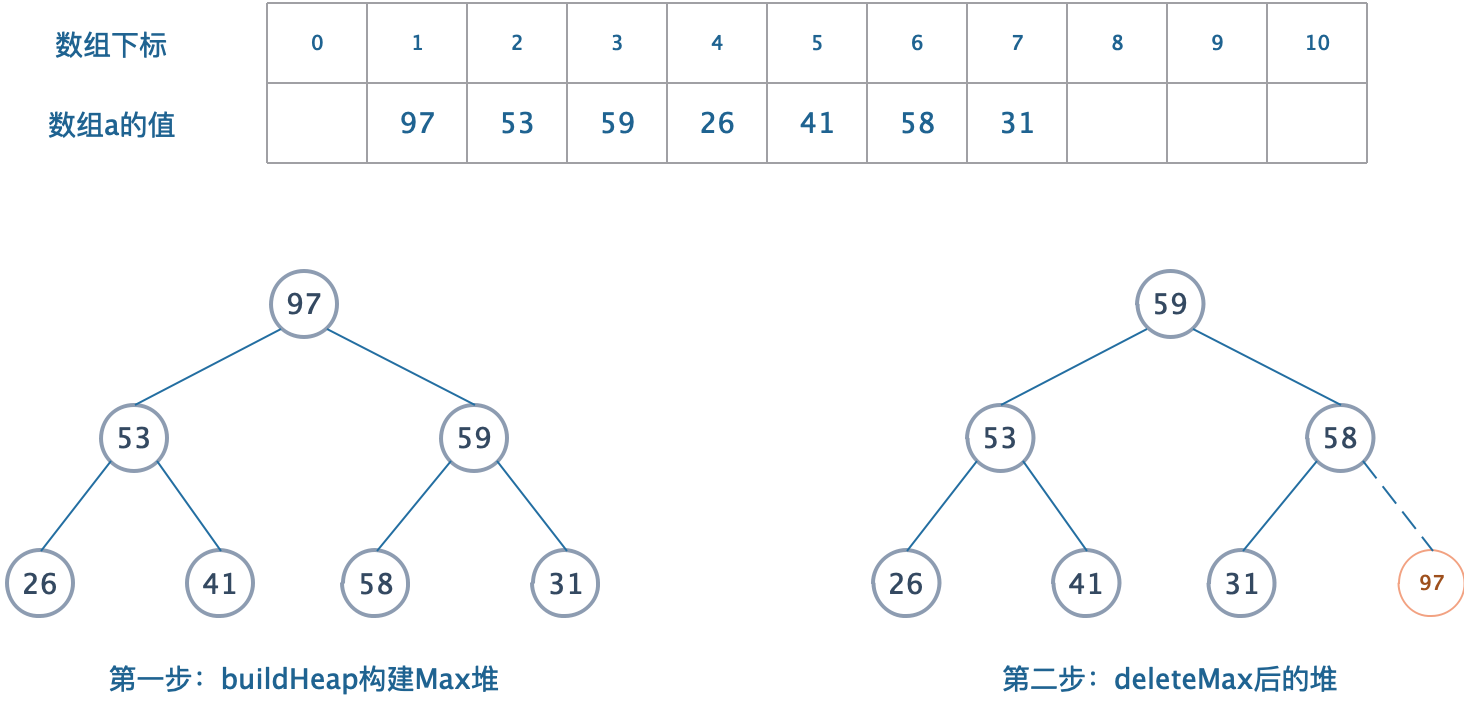

圖解描述

? 我們對數組a進行堆排序，采用根節點存放最大值（最大最小都一樣）并且避免使用第二個數組。

• 構建一個Max堆，最大值在根節點，父節點必定比子節點大。
• deleteMax，堆縮小1。
• 將剛剛刪除的元素放在空出來的位置。
• 依次類推，我們借助二叉堆一個重要的特性：刪除時，總是空出最后一個元素。這是為了保持它是一個完全二叉樹。
  

以上做法，我們避免使用第二個數組，而是直接在第一個數組中構建一個堆。然后將堆排序！

二、算法分析

? 堆排序耗費的時間可以分為2個部分。第一階段構建堆，第二階段是循環刪除根元素(deleteMax)。

? 第一階段：從堆的性質我們可以知道，構建N個元素的堆，需要2N次比較。（這是因為堆的性質是父節點大于子節點，所以要選出父節點，需要根左右子節點相互比較）

? 第二階段：循環deleteMax。第\(i\)次deleteMax最多用到\(2\lfloor logi \rfloor\)次比較，這個時間來自于堆的deleteMax時間分析，刪除最大值之后，我們需要重新構建堆，那么就需要最后一個位置放入根節點所在的空穴（根節點作為最大值已經被刪除，只剩下空穴一個）中，然后采用下沉的方式，將它放到合適的位置，重新構建堆只需要滿足父節點大于子節點，所以下沉過程只需要根左子節點和右子節點比較，而二叉樹的高是\(logN\)。

? 所以總時間是:
\[ 第二階段+第一階段時間 \\ 2(\sum_{i=1}^{N}logi )+2N\\ =2(log1+log2+···+logN)+2N\\ =2(log(1*2*3*···*N))+2N\\ =2(logN!)+2N\\ =2(log(\sqrt{2\pi N}\frac{N^N}{e^N})+2N\\ =2(\frac{1}{2}log(2\pi)+\frac{1}{2}logN + NlogN -Nloge)+2N \\ =O(2NlogN-O(N)) \]

關于堆的構建和刪除可以參照：https://www.cnblogs.com/dhcao/p/10591282.html

?

? 堆排序的時間是：\(O(2NlogN-O(N))\)

三、代碼地址

https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterSeven/HeasportEx.java