經典排序算法在面試中占有很大的比重,也是基礎,為了未雨綢繆,在寒假里整理并用Python實現了七大經典排序算法,包括冒泡排序,插入排序,選擇排序,希爾排序,歸并排序,快速排序,堆排序。希望能幫助到有需要的同學。之所以用Python實現,主要是因為它更接近偽代碼,能用更少的代碼實現算法,更利于理解。
本篇博客所有排序實現均默認從小到大。
一、冒泡排序 BubbleSort
介紹:
冒泡排序的原理非常簡單,它重復地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。
步驟:
- 比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
- 對第0個到第n-1個數據做同樣的工作。這時,最大的數就“浮”到了數組最后的位置上。
- 針對所有的元素重復以上的步驟,除了最后一個。
- 持續每次對越來越少的元素重復上面的步驟,直到沒有任何一對數字需要比較。
源代碼:(python實現)
1 | def bubble_sort(arry): |
?
運行上面的代碼有錯誤,
下面是自己寫的,經過驗證:
__author__ = 'xy'
def bubble_sort(arry):
n=len(arry)
for i in range(n-1,0,-1):
flag=1
for j in range(0,i):
if arry[j] > arry[j+1]:
arry[j],arry[j+1] = arry[j+1],arry[j]
flag=0
if flag:
break
return arry
arry=[5,4,5,7,9,3,2,3,4]
print arry
bubble_sort(arry)
print arry
?
不過針對上述代碼還有兩種優化方案。
優化1:某一趟遍歷如果沒有數據交換,則說明已經排好序了,因此不用再進行迭代了。用一個標記記錄這個狀態即可。
優化2:記錄某次遍歷時最后發生數據交換的位置,這個位置之后的數據顯然已經有序,不用再排序了。因此通過記錄最后發生數據交換的位置就可以確定下次循環的范圍了。
這兩種優化方案的實現可以詳見這里。
二、選擇排序 SelectionSort
介紹:
選擇排序無疑是最簡單直觀的排序。它的工作原理如下。
步驟:
- 在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
- 再從剩余未排序元素中繼續尋找最小(大)元素,然后放到已排序序列的末尾。
- 以此類推,直到所有元素均排序完畢。
源代碼:(python實現)
1 | def select_sort(ary): |
?
三、插入排序 InsertionSort
介紹:
插入排序的工作原理是,對于每個未排序數據,在已排序序列中從后向前掃描,找到相應位置并插入。
步驟:
- 從第一個元素開始,該元素可以認為已經被排序
- 取出下一個元素,在已經排序的元素序列中從后向前掃描
- 如果被掃描的元素(已排序)大于新元素,將該元素后移一位
- 重復步驟3,直到找到已排序的元素小于或者等于新元素的位置
- 將新元素插入到該位置后
- 重復步驟2~5
排序演示:
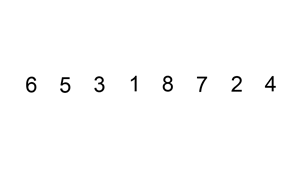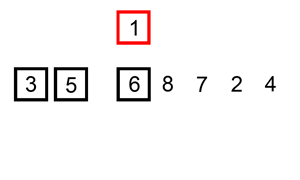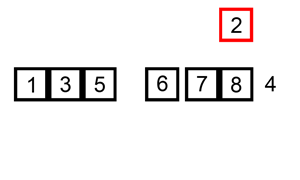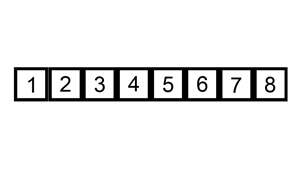
源代碼:(python實現)
1 | def insert_sort(ary): |
?
四、希爾排序 ShellSort
介紹:
希爾排序,也稱遞減增量排序算法,實質是分組插入排序。由 Donald Shell 于1959年提出。希爾排序是非穩定排序算法。
希爾排序的基本思想是:將數組列在一個表中并對列分別進行插入排序,重復這過程,不過每次用更長的列(步長更長了,列數更少了)來進行。最后整個表就只有一列了。將數組轉換至表是為了更好地理解這算法,算法本身還是使用數組進行排序。
例如,假設有這樣一組數[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我們以步長為5開始進行排序,我們可以通過將這列表放在有5列的表中來更好地描述算法,這樣他們就應該看起來是這樣:
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
然后我們對每列進行排序:
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
將上述四行數字,依序接在一起時我們得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。這時10已經移至正確位置了,然后再以3為步長進行排序:
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
排序之后變為:
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
最后以1步長進行排序(此時就是簡單的插入排序了)。
源代碼:(python實現)
1 | def shell_sort(ary): |
?
上面源碼的步長的選擇是從n/2開始,每次再減半,直至為0。步長的選擇直接決定了希爾排序的復雜度。在維基百科上有對于步長串行的詳細介紹。
五、歸并排序 MergeSort
介紹:
歸并排序是采用分治法的一個非常典型的應用。歸并排序的思想就是先遞歸分解數組,再合并數組。
先考慮合并兩個有序數組,基本思路是比較兩個數組的最前面的數,誰小就先取誰,取了后相應的指針就往后移一位。然后再比較,直至一個數組為空,最后把另一個數組的剩余部分復制過來即可。
再考慮遞歸分解,基本思路是將數組分解成left和right,如果這兩個數組內部數據是有序的,那么就可以用上面合并數組的方法將這兩個數組合并排序。如何讓這兩個數組內部是有序的?可以再二分,直至分解出的小組只含有一個元素時為止,此時認為該小組內部已有序。然后合并排序相鄰二個小組即可。
排序演示:
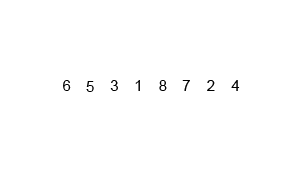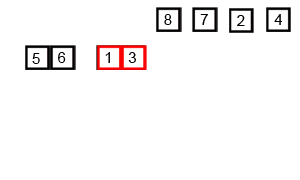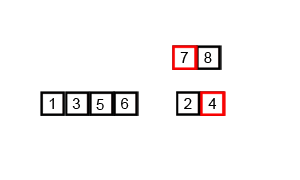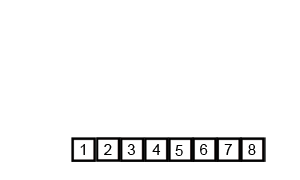
源代碼:(python實現)
1 | def merge_sort(ary): |
?
六、快速排序 QuickSort
介紹:
快速排序通常明顯比同為Ο(n log n)的其他算法更快,因此常被采用,而且快排采用了分治法的思想,所以在很多筆試面試中能經常看到快排的影子。可見掌握快排的重要性。
步驟:
- 從數列中挑出一個元素作為基準數。
- 分區過程,將比基準數大的放到右邊,小于或等于它的數都放到左邊。
- 再對左右區間遞歸執行第二步,直至各區間只有一個數。
排序演示:
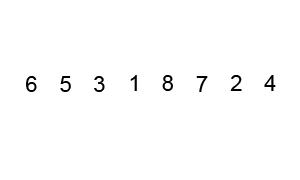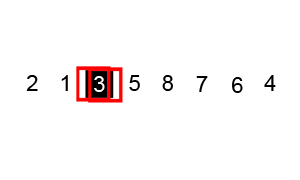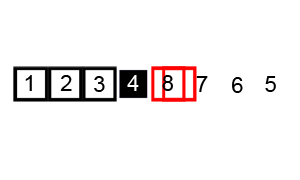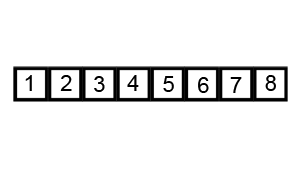
源代碼:(python實現)
1 | def quick_sort(ary): |
?
七、堆排序 HeapSort
介紹:
堆排序在 top K 問題中使用比較頻繁。堆排序是采用二叉堆的數據結構來實現的,雖然實質上還是一維數組。二叉堆是一個近似完全二叉樹 。
二叉堆具有以下性質:
- 父節點的鍵值總是大于或等于(小于或等于)任何一個子節點的鍵值。
- 每個節點的左右子樹都是一個二叉堆(都是最大堆或最小堆)。
步驟:
-
構造最大堆(Build_Max_Heap):若數組下標范圍為0~n,考慮到單獨一個元素是大根堆,則從下標
n/2開始的元素均為大根堆。于是只要從n/2-1開始,向前依次構造大根堆,這樣就能保證,構造到某個節點時,它的左右子樹都已經是大根堆。 -
堆排序(HeapSort):由于堆是用數組模擬的。得到一個大根堆后,數組內部并不是有序的。因此需要將堆化數組有序化。思想是移除根節點,并做最大堆調整的遞歸運算。第一次將
heap[0]與heap[n-1]交換,再對heap[0...n-2]做最大堆調整。第二次將heap[0]與heap[n-2]交換,再對heap[0...n-3]做最大堆調整。重復該操作直至heap[0]和heap[1]交換。由于每次都是將最大的數并入到后面的有序區間,故操作完后整個數組就是有序的了。 -
最大堆調整(Max_Heapify):該方法是提供給上述兩個過程調用的。目的是將堆的末端子節點作調整,使得子節點永遠小于父節點 。
排序演示:

源代碼:(python實現)
1 | def heap_sort(ary) : |
?
總結
下面為七種經典排序算法指標對比情況:








)






)


)

