HMM簡介
對于算法愛好者來說，隱馬爾可夫模型的大名那是如雷貫耳。那么，這個模型到底長什么樣？具體的原理又是什么呢？有什么具體的應用場景呢？本文將會解答這些疑惑。
本文將通過具體形象的例子來引入該模型，并深入探究隱馬爾可夫模型及Viterbi算法，希望能對大家有所啟發。
隱馬爾可夫模型（HMM，hidden Markov model）是可用于標注問題的統計學模型，描述由隱藏的馬爾可夫鏈隨機生成觀測序列的過程，屬于生成模型。HMM模型在實際的生活和生產中有著廣泛的應用，包括語音識別，自然語言處理，生物信息，模式識別等領域。
?
引入
某天，你的女神告訴你說，她放假三天，將要去上海游玩，準備去歡樂谷、迪士尼和外灘（不一定三個都會去）。
她呢，會選擇在這三個地方中的某幾個逗留并決定是否購物，而且每天只待在一個地方。根據你對她的了解，知道她去哪個地方，僅取決于她去的上一個地方，且是否購物的概率僅取決于她去的地方。已知她去的三個地方的轉移概率表如下：
?
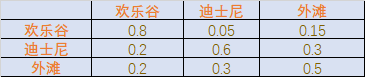
稍微對這個表格做些說明，比如第一行，前一天去了歡樂谷后，第二天還待在歡樂谷的概率為0.8，去迪士尼的概率為0.05，去外灘的概率為0.15。
??她在每個地方的購物概率為：
?
| 地點 | 購物概率 |
|---|---|
| 歡樂谷 | 0.1 |
| 迪士尼 | 0.8 |
| 外灘 | 0.3 |
在出發的時候，她跟你說去每個地方的可能性相同。后來，放假回來后，你看了她的朋友圈，發現她的購物情況如下：第一天不購物，第二三天都購物了。于是，你很好奇，她這三天都去了哪些地方。
??怎么樣，聰明的你能求解出來嗎？
HMM的模型參數
接下來，我們將會介紹隱馬爾可夫模型（HMM）。
??隱馬爾可夫模型是關于時序的概率模型，描述由一個隱藏的馬爾可夫鏈隨機生成不可觀測的狀態隨機序列，再由各個狀態生成一個觀測而產生觀測隨機序列的過程。隱藏的馬爾可夫鏈隨機生成的狀態的序列，稱為狀態序列；每個狀態生成一個觀測，而由此產生的觀測的隨機序列，稱為觀測序列。序列的每一個位置又可以看作是一個時刻。
??隱馬爾可夫模型由初始概率分布、狀態轉移概率分布以及觀測概率分布確定。隱馬爾可夫模型的形式定義如下：
??設Q是所有可能的狀態的集合，V是所有可能的觀測的集合，也就是說，Q是不可見的，而V是可見的，是我們觀測到的可能結果。
? ? ? ? ? ? ? ? ? ? ? ?
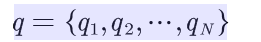
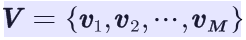
其中，N是可能的狀態數，M是可能的觀測數。
??在剛才的例子中，Q是不可見的狀態集合，應為
，而V是可以觀測的集合，應為V={購物，不購物}。
??I是長度為T的狀態序列，O是對應的觀測序列。
在剛才的例子中，I這個序列是我們需要求解的，即女生去了哪些地方，而O是你知道的序列，O={不購物，購物，購物}。
??A是狀態轉移概率矩陣：
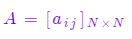其中，
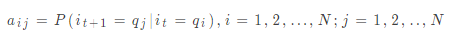
是在時刻t處于狀態q_i的條件下在時刻t+1轉移到狀態q_j的概率。在剛才的例子中，轉移概率矩陣為：
?
?
?
?
?
B是觀測概率矩陣：
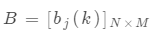
其中，
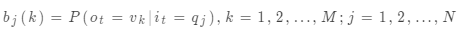
是在時刻t處于狀態q_j的條件下生成觀測v_k的概率。在剛才的例子中：
?
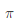是初始狀態概率向量
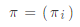,其中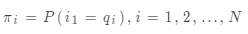
是時刻t=1處于狀態q_j的概率。在剛才的例子中，?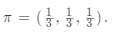
綜上，我們已經講完HMM中的基本概念。同時，我們可以知道，隱馬爾可夫模型由初始狀態概率向量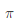，狀態轉移概率矩陣A，和觀測概率矩陣B決定。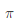和A決定狀態序列，B決定觀測序列。因此，隱馬爾可夫模型
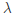可用三元符號表示，即
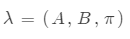
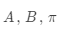稱為HMM的三要素。
當然，隱馬爾可夫模型之所以被稱為馬爾可夫模型，是因為它使用了兩個基本的假設，其中之一為馬爾可夫假設。它們分別是：
-
齊次馬爾科夫假設，即假設隱藏的馬爾可夫鏈在任意時刻t的狀態只依賴于其前一時刻的狀態，與其他時刻的狀態及觀測無關，也與時刻t無關。
-
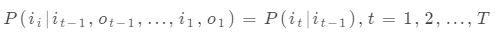
觀測獨立性假設，即假設任意時刻的觀測只依賴于該時刻的馬爾可夫鏈的狀態，與其他觀測及狀態無關。
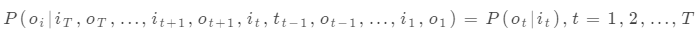
??在剛才的假設中，我們對應的兩個假設分別為：她去哪個地方，僅取決于她去的上一個地方；是否購物的概率僅取決于她去的地方。前一個條件為齊次馬爾科夫假設，后一個條件為觀測獨立性假設。
??以上，我們就介紹了HMM的基本概念及假設。而HMM的三個基本問題如下：
1. 概率計算問題。給定模型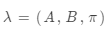
和觀測序列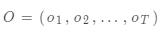
,計算在模型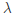下觀測序列O出現的概率
.
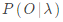2. 學習問題。已知觀測序列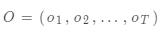，估計模型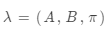參數，使得在該模型下觀測序列概率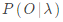最大。
3. 預測問題。已知模型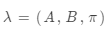和觀測序列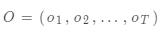，求對給定觀測序列條件概率
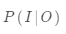最大的狀態序列
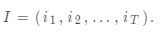即給定觀測序列，求最有可能的對應的狀態序列。
??上面的例子即為HMM的第三個基本問題，也就是，給定觀測序列{不購物，購物，購物}，結果最有可能的狀態序列，即游玩的地方。
Viterbi算法
求解HMM的第三個基本問題，會用到大名鼎鼎的維特比算法（Viterbi Algorithm）。
??維特比算法以安德魯·維特比（Andrew Viterbi）命名，是現代數字通信中最常用的算法，同時也是很多自然語言處理采用的解碼算法。可以毫不夸張地講，維特比是對我們的生活影音力最大的科學家之一，因為基于CDMA的3G移動通信標準主要就是他和厄文·雅各布（Irwin Mark Jacobs）創辦的高通公司（Qualcomm）指定的。
??維特比算法是一個特殊但應用最廣的動態規劃（dynamic programming）算法，利用動態規劃，可以解決任何一個圖中的最短路徑問題，同時，它也是求解HMM描述的第三個基本問題的算法。
??在維特比算法中，需要引入兩個變量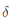
和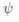
。定義在時刻t狀態i的所有單個路徑
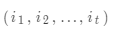中概率最大值為
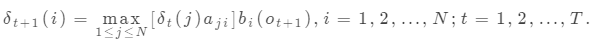
定義在時刻t狀態為i的所有單個路徑
中概率最大的路徑的第i-1個節點為
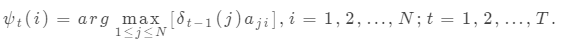
??下面是維特比算法在HMM的第三個基本問題的算法：
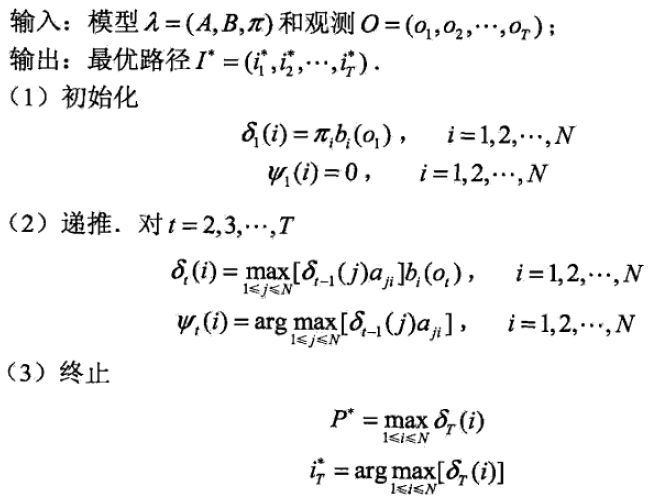
Python代碼實現
#?-*-?coding:?utf-8?-*-
#?HMM.py
#?Using?Vertibi?algorithmimport?numpy?as?npdef?Viterbi(A,?B,?PI,?V,?Q,?obs):N?=?len(Q)T?=?len(obs)delta?=?np.array([[0]?*?N]?*?T,?dtype=np.float64)phi?=?np.array([[0]?*?N]?*?T,?dtype=np.int64)#?初始化for?i?in?range(N):delta[0,?i]?=?PI[i]*B[i][V.index(obs[0])]phi[0,?i]?=?0#?遞歸計算for?i?in?range(1,?T):for?j?in?range(N):tmp?=?[delta[i-1,?k]*A[k][j]?for?k?in?range(N)]delta[i,j]?=?max(tmp)?*?B[j][V.index(obs[i])]phi[i,j]?=?tmp.index(max(tmp))#?最終的概率及節點P?=?max(delta[T-1,?:])I?=?int(np.argmax(delta[T-1,?:]))#?最優路徑pathpath?=?[I]for?i?in?reversed(range(1,?T)):end?=?path[-1]path.append(phi[i,?end])hidden_states?=?[Q[i]?for?i?in?reversed(path)]return?P,?hidden_statesdef?main():#?狀態集合Q?=?('歡樂谷',?'迪士尼',?'外灘')#?觀測集合V?=?['購物',?'不購物']#?轉移概率:?Q?->?QA?=?[[0.8,?0.05,?0.15],[0.2,?0.6,?0.2],[0.2,?0.3,?0.5]]#?發射概率,?Q?->?VB?=?[[0.1,?0.9],[0.8,?0.2],[0.3,?0.7]]#?初始概率PI?=?[1/3,?1/3,?1/3]#?觀測序列obs?=?['不購物',?'購物',?'購物']P,?hidden_states?=?Viterbi(A,B,PI,V,Q,obs)print('最大的概率為:?%.5f.'%P)print('隱藏序列為：%s.'%hidden_states)main() ?
輸出結果如下：
最大的概率為:?0.02688.
隱藏序列為：['外灘',?'迪士尼',?'迪士尼']. ?
現在，你有很大的把握可以確定，你的女神去了外灘和迪士尼。
?
參考文獻
-
一文搞懂HMM（隱馬爾可夫模型）：https://www.cnblogs.com/skyme/p/4651331.html
-
李航《統計學習方法》 清華大學出版社
-
HMM與分詞、詞性標注、命名實體識別：http://www.hankcs.com/nlp/hmm-and-segmentation-tagging-named-entity-recognition.html
-
Hidden Markov Models 1: http://docplayer.net/21306742-Hidden-markov-models-1.html
-
吳軍 《數學之美》 人民郵電出版社
)