一、▽ 算子、點積、叉積
l▽ 算子叫“del”算子，即<< span="">?/?x,?/?y,?/?z>,可以理解為一個符號向量，向量里的元素是偏微分運算符號，沒有任何具體意義，只是一個表示方法。
ln維向量的內積定義如下：
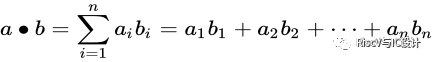
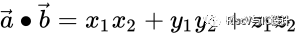(常用的3維空間定義)
?? 對于二維和三維空間，點積的幾何定義為：
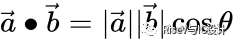
這個運算可以簡單地理解為：在點積運算中，第一個向量投影到第二個向量上
l向量積，數學中又稱外積、叉積，物理中稱矢積、叉乘，是一種在向量空間中向量的二元運算。與點積不同，它的運算結果是一個向量而不是一個標量,其常見的各種定義如下:
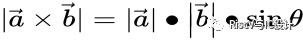
名稱 | 標積/內積/數量積/點積 | 矢積/外積/向量積/叉積 |
運算式 | a·b=|a||b|·cosθ | a×b=c，其中|c|=|a||b|·sinθ，c的方向遵守右手定則 |
幾何意義 | 向量a在向量b方向上的投影與向量b的模的乘積 | c是垂直a、b所在平面，且以|b|·sinθ為高、|a|為底的平行四邊形的面積 |
運算結果的區別 | 標量(常用于物理)/數量(常用于數學) | 矢量(常用于物理)/向量(常用于數學) |
二、梯度、散度、旋度
有了▽算子，梯度、散度、旋度都可以用▽向量來表示。
1.梯度 gradient
函數f(x,y,z)(標量)的梯度可以理解為▽向量與函數f的乘積,即：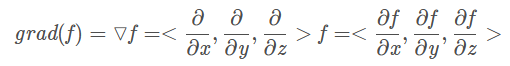
梯度的定義:在標量場f中的一點處存在一個矢量grad(f),該矢量方向為f在該點處變化率最大的方向,其模也等于這個最大變化率的數值,則矢量grad(f)稱為標量場f的梯度。因此,梯度是矢量。
2.散度 divergence
散度可用于表征空間各點矢量場發散的強弱程度，物理上，散度的意義是場的有源性。當div F>0 ，表示該點有散發通量的正源(發散源)；當div F<0 表示該點有吸收通量的負源(洞或匯)；當div F=0，表示該點無源。
散度可以表示為▽向量與矢量場F的點積,散度是標量：
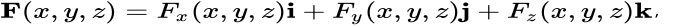
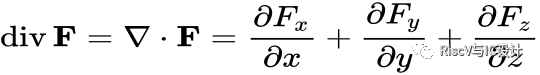
l運算法則
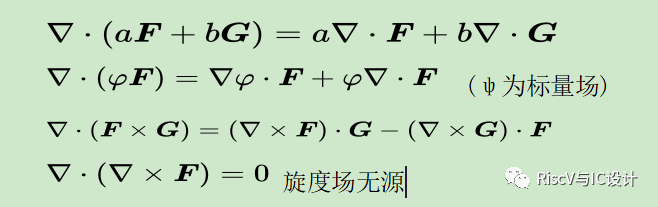
l不同坐標系下的散度表達式
矢量V的散度在笛卡爾坐標(直角坐標系)下的表達式：
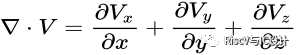
矢量V的散度在球坐標下的表達式：
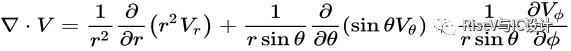
矢量V的散度在柱坐標下的表達式：
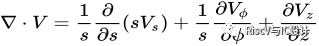
3.旋度 curl
定義向量場的旋度，首先要引入環量(或稱為旋渦量)的概念。給定一個三維空間中的向量場u以及一個簡單閉合有向(平面)曲線L,u沿著曲線的環量就是u沿著路徑的閉合曲線L的點積的積分：
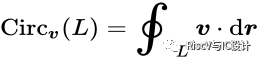
其中曲線上的線元 dr是矢量，方向是曲線的切線方向，其正方向規定為使得閉合曲線所包圍的面積在它的左側。
環量和通量一樣，是描述向量場的重要參數。某個區域中的環量不等于零，說明這個區域中的向量場表現出環繞某一點或某一區域旋轉的特性。旋度則是局部地描述這一特性的方法。為了描述一個向量場在一點附近的環量，將閉合曲線收小，使它包圍的面元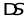
的面積趨于零。向量場u沿著L的環量和面元的比值在趨于零時候的極限值：
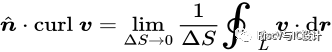
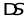為的所在平面的法向量
向量場的旋度記作：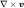
l直角坐標系
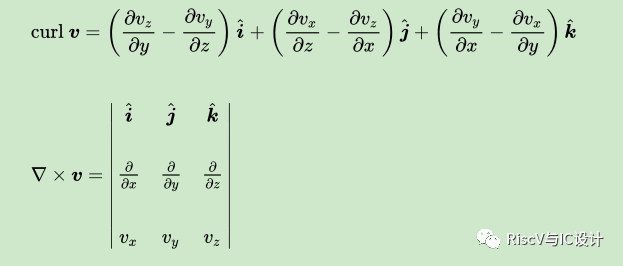
l圓柱坐標系
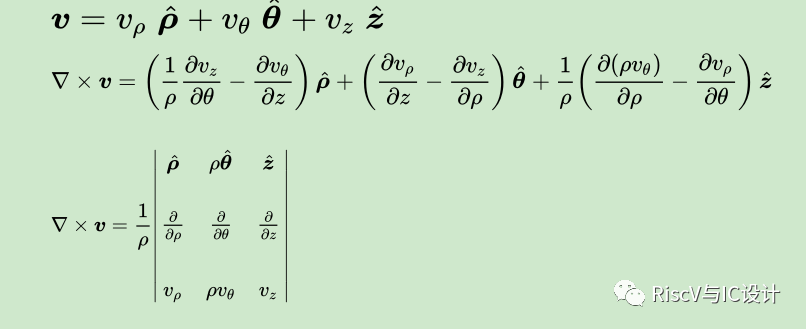
l球坐標系
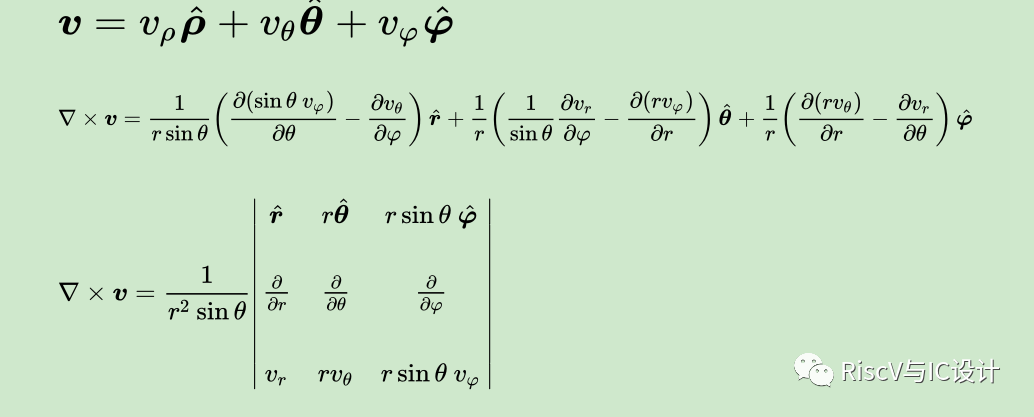
三、線積分、面積分、散度定律、斯托克斯定理
l線積分
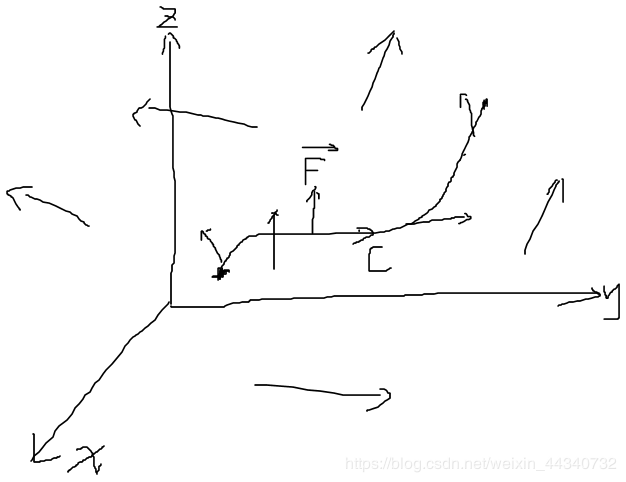
上圖中，F是空間中的矢量場， C是含有方向的線段。則?F對C的積分(理解為物理上的功)可以表示為：
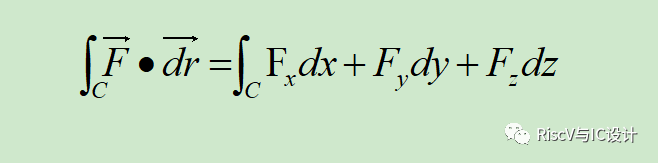
l面積分
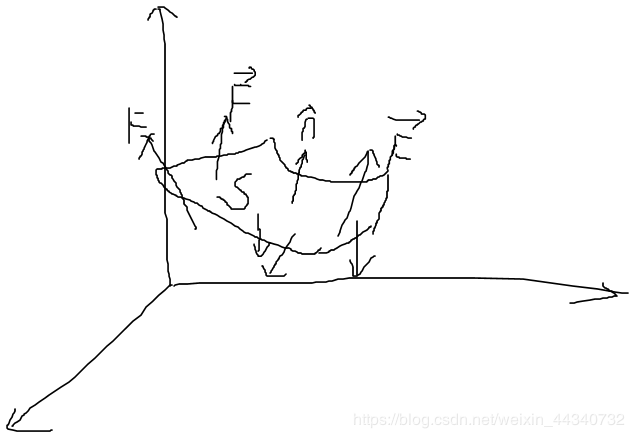
上圖中，S表示空間中一個曲面，n?表示曲面的法向量(兩個方向中選一個)。則矢量?F對曲面S的積分表示通量(Flux)，即：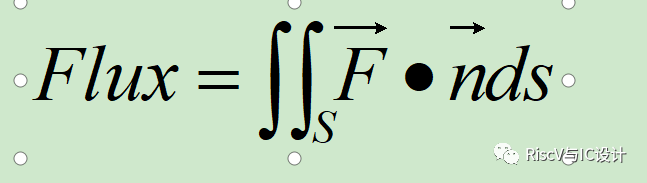
lGauss-Green 定理(散度定理)
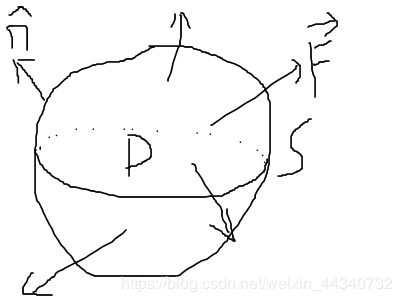
如果S是空間中的封閉曲面，包裹了一個區域D，法向量n?
n^向外，?F在D的每一個區域都定義且可微，則下式成立：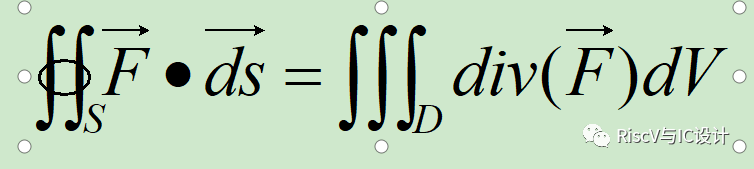
l斯托克斯定理(Stokes)定理
如果C是一個封閉曲線，S是以C為邊的任意曲面，F在S上有定義，n?為滿足右手定則方向向外，則有如下公式：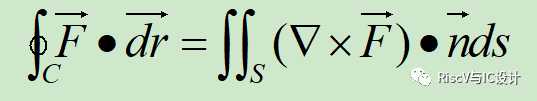
四、麥克斯韋方程組
1. 積分形式的麥克斯韋方程組是描述電磁場在某一體積或某一面積內的數學模型。表達式為：
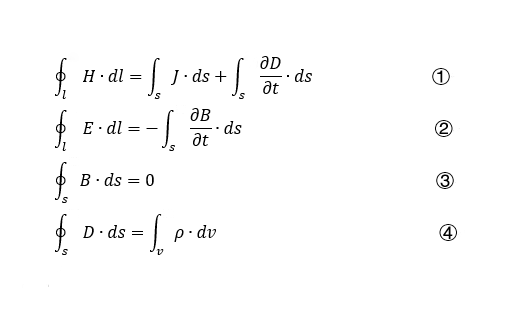
l式①是由安培環路定律推廣而得的全電流定律，其含義是：磁場強度H沿任意閉合曲線的線積分，等于穿過此曲線限定面積的全電流。等號右邊第一項是傳導電流．第二項是位移電流。
l式②是法拉第電磁感應定律的表達式，它說明電場強度E沿任意閉合曲線的線積分等于穿過由該曲線所限定面積的磁通對時間的變化率的負值。這里提到的閉合曲線，并不一定要由導體構成，它可以是介質回路，甚至只是任意一個閉合輪廓。
l式③表示磁通連續性原理，說明對于任意一個閉合曲面，有多少磁通進入曲面就有同樣數量的磁通離開。即B線是既無始端又無終端的；同時也說明并不存在與電荷相對應的磁荷。
l式④是高斯定律的表達式，說明在時變的條件下，從任意一個閉合曲面出來的D的凈通量，應等于該閉曲面所包圍的體積內全部自由電荷之總和。
2. 微分形式的麥克斯韋方程組。微分形式的麥克斯韋方程是對場中每一點而言的。應用del算子，可以把它們寫成
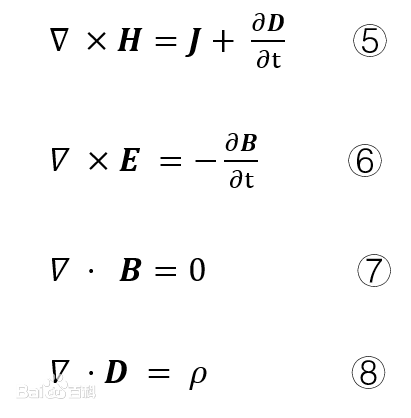
l式⑤是全電流定律的微分形式，它說明磁場強度H的旋度等于該點的全電流密度(傳導電流密度J與位移電流密度之和)，即磁場的漩渦源是全電流密度，位移電流與傳導電流一樣都能產生磁場。
l式⑥是法拉第電磁感應定律的微分形式，說明電場強度E的旋度等于該點磁通密度B的時間變化率的負值，即電場的渦旋源是磁通密度的時間變化率。
l式⑦是磁通連續性原理的微分形式，說明磁通密度B的散度恒等于零，即B線是無始無終的。也就是說不存在與電荷對應的磁荷。
l式⑧是靜電場高斯定律的推廣，即在時變條件下，電位移D的散度仍等于該點的自由電荷體密度。
除了上述四個方程外，還需要有媒質的本構關系式，才能最終解決場量的求解問題。式中ε是媒質的介電常數，μ是媒質的磁導率，σ是媒質的電導率：
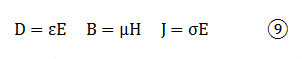
麥克斯韋方程組表格：
