什么是m叉樹_不懂數據庫索引的底層原理？那是因為你心里沒點b樹

前幾天下班回到家后正在處理一個白天沒解決的bug，廁所突然傳來對象的聲音：
對象：xx，你有《時間簡史》嗎？
我：我去！妹子，你這啥癖好啊，我有時間也不會去撿屎啊！
對象：...人家說的是霍金的科普著作《時間簡史》，是一本書啦！
我：哦，那我沒有...
對象：人家想看誒，你明天幫我去圖書館借一本吧...
我：我明天還要改...
對象：你是不是不愛我了，分手！
我：我一大早就去~

第二天一大早我就到了圖書館，剛進門就看到一個索引牌，標識著不同樓層的功能，這樣我很快能定位到我要找的目標所在的樓層了。

我到樓上后又看到每排的書架上又對書的分類進行了細分，這樣我能更快的定位到我要找的書具體在哪個書架！

并且每個樓層都有一臺查詢終端，輸入書名就能查到對應的唯一標識“索書號”，類似于P159-49/164這樣的一個編碼，書架上的書都是按照這個編碼進行排序的！有了這個編碼再去對應的書架上，很快就能找到對應的書在書架的具體位置了。

不到十分鐘，我就從圖書館借好書出來了。

這么大的圖書館，我為什么能在這么短的時間內找到我要的書？如果這些書是雜亂無章的堆放，或者沒有任何標識的放在書架，我還能這么快的找到嗎？

這不禁讓我想到了我們開發中用到的數據庫，圖書館的書就類似我們數據表中的數據，樓層索引牌、書架分類標識、索書號就類似我們查找數據的索引。

那我們常用的數據庫的索引底層的一個數據結構是什么樣的呢？想到這里我又回到圖書館借了一本《數據庫從入門到放棄》！

要了解數據庫索引的底層原理，我們就得先了解一種叫樹的數據結構，而樹中很經典的一種數據結構就是二叉樹！所以下面我們就從二叉樹到平衡二叉樹，再到B-樹，最后到B+樹來一步一步了解數據庫索引底層的原理！

二叉樹（Binary Search Trees）

二叉樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”（left subtree）和“右子樹”（right subtree）。二叉樹常被用于實現二叉查找樹和二叉堆。二叉樹有如下特性：

1、每個結點都包含一個元素以及n個子樹，這里0≤n≤2。
2、左子樹和右子樹是有順序的，次序不能任意顛倒。左子樹的值要小于父結點，右子樹的值要大于父結點。

光看概念有點枯燥，假設我們現在有這樣一組數[35 27 48 12 29 38 55]，順序的插入到一個數的結構中，步驟如下：

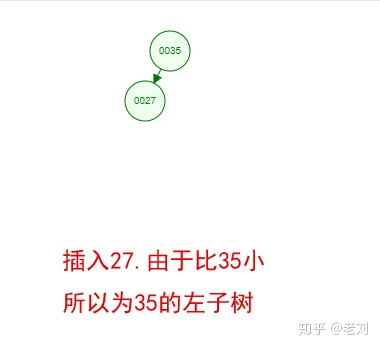
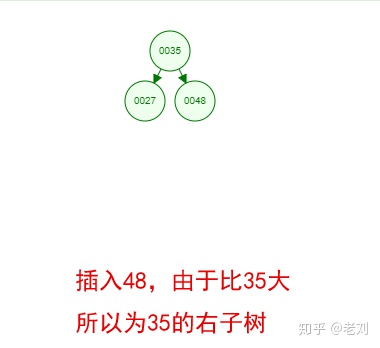
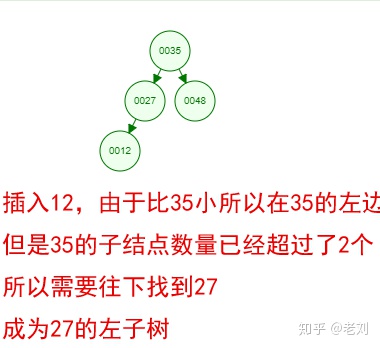
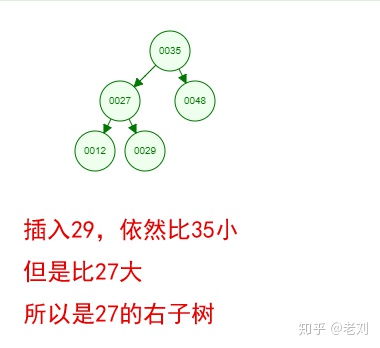
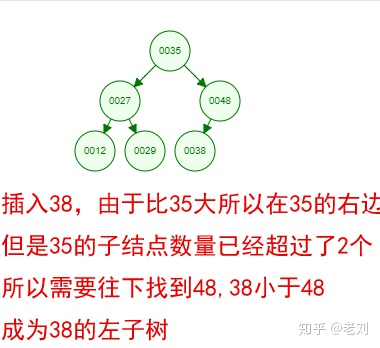
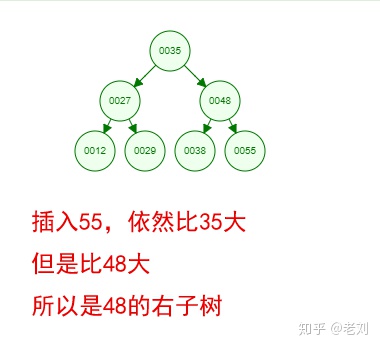
好了，這就是一棵二叉樹啦！我們能看到，經通過一系列的插入操作之后，原本無序的一組數已經變成一個有序的結構了，并且這個樹滿足了上面提到的兩個二叉樹的特性！

但是如果同樣是上面那一組數，我們自己升序排列后再插入，也就是說按照[12 27 29 35 38 48 55]的順序插入，會怎么樣呢？

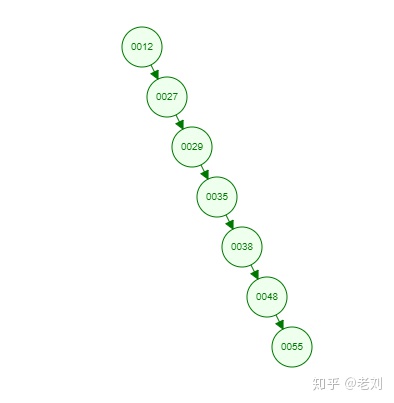
由于是升序插入，新插入的數據總是比已存在的結點數據都要大，所以每次都會往結點的右邊插入，最終導致這棵樹嚴重偏科！！！上圖就是最壞的情況，也就是一棵樹退化為一個線性鏈表了，這樣查找效率自然就低了，完全沒有發揮樹的優勢了呢！
為了較大發揮二叉樹的查找效率，讓二叉樹不再偏科，保持各科平衡，所以有了平衡二叉樹！

平衡二叉樹 (AVL Trees)

平衡二叉樹是一種特殊的二叉樹，所以他也滿足前面說到的二叉樹的兩個特性，同時還有一個特性：

它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一棵平衡二叉樹。

大家也看到了前面[35 27 48 12 29 38 55]插入完成后的圖，其實就已經是一顆平衡二叉樹啦。

那如果按照[12 27 29 35 38 48 55]的順序插入一顆平衡二叉樹，會怎么樣呢？我們看看插入以及平衡的過程：

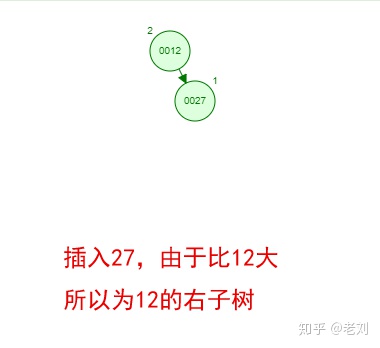
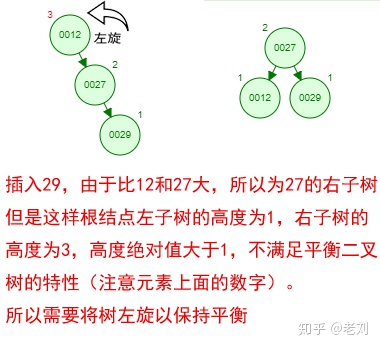
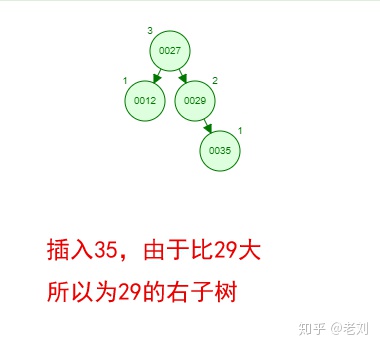
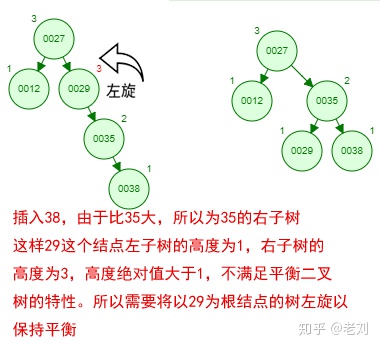
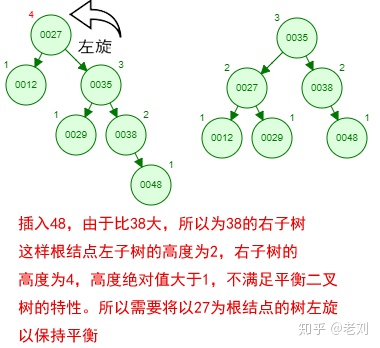
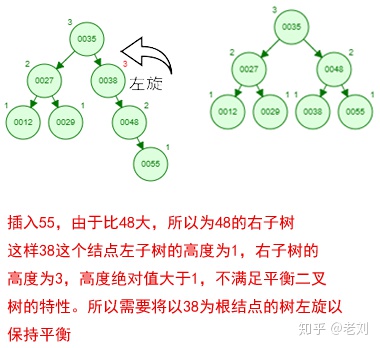
這棵樹始終滿足平衡二叉樹的幾個特性而保持平衡！這樣我們的樹也不會退化為線性鏈表了！我們需要查找一個數的時候就能沿著樹根一直往下找，這樣的查找效率和二分法查找是一樣的呢！

一顆平衡二叉樹能容納多少的結點呢？這跟樹的高度是有關系的，假設樹的高度為h，那每一層最多容納的結點數量為2^(n-1)，整棵樹最多容納節點數為2^0+2^1+2^2+...+2^(h-1)。這樣計算，100w數據樹的高度大概在20左右，那也就是說從有著100w條數據的平衡二叉樹中找一個數據，最壞的情況下需要20次查找。如果是內存操作，效率也是很高的！但是我們數據庫中的數據基本都是放在磁盤中的，每讀取一個二叉樹的結點就是一次磁盤IO，這樣我們找一條數據如果要經過20次磁盤的IO？那性能就成了一個很大的問題了！那我們是不是可以把這棵樹壓縮一下，讓每一層能夠容納更多的節點呢？雖然我矮，但是我胖啊...

B-Tree

這顆矮胖的樹就是B-Tree，注意中間是杠精的杠而不是減，所以也不要讀成B減Tree了~

那B-Tree有哪些特性呢？一棵m階的B-Tree有如下特性：

1、每個結點最多m個子結點。
2、除了根結點和葉子結點外，每個結點最少有m/2（向上取整）個子結點。
3、如果根結點不是葉子結點，那根結點至少包含兩個子結點。
4、所有的葉子結點都位于同一層。
5、每個結點都包含k個元素（關鍵字），這里m/2≤k<m，這里m/2向下取整。
6、每個節點中的元素（關鍵字）從小到大排列。
7、每個元素（關鍵字）字左結點的值，都小于或等于該元素（關鍵字）。右結點的值都大于或等于該元素（關鍵字）。

是不是感覺跟丈母娘張口問你要彩禮一樣，列一堆的條件，而且每一條都讓你很懵逼！下面我們以一個[0,1,2,3,4,5,6,7]的數組插入一顆3階的B-Tree為例，將所有的條件都串起來，你就明白了！

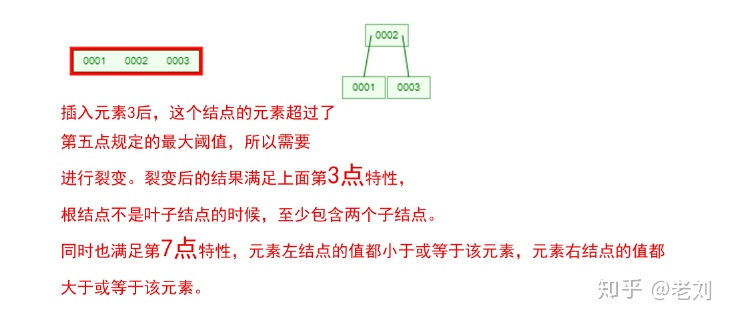
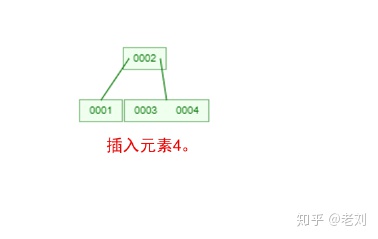
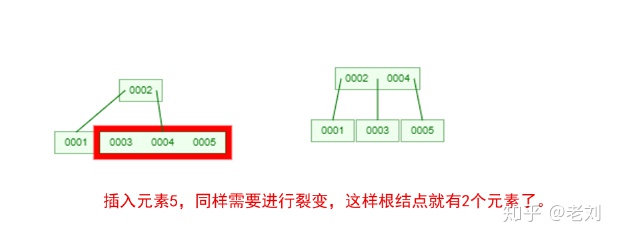
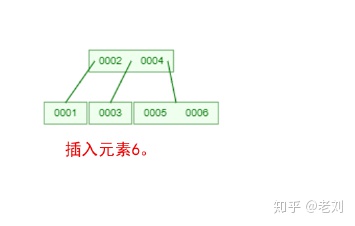
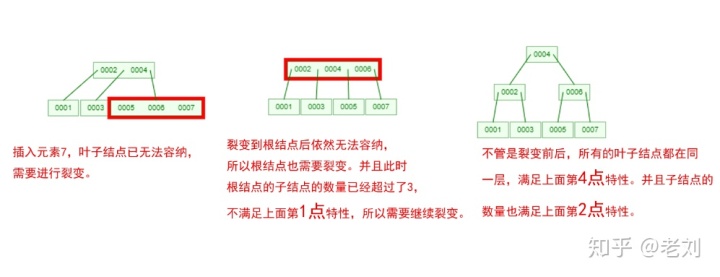
那么，你是否對B-Tree的幾點特性都清晰了呢？在二叉樹中，每個結點只有一個元素。但是在B-Tree中，每個結點都可能包含多個元素，并且非葉子結點在元素的左右都有指向子結點的指針。

如果需要查找一個元素，那流程是怎么樣的呢？我們看下圖，如果我們要在下面的B-Tree中找到關鍵字24，那流程如下：

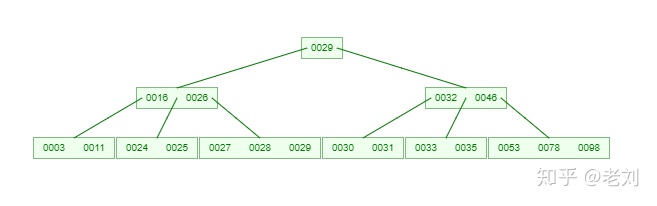
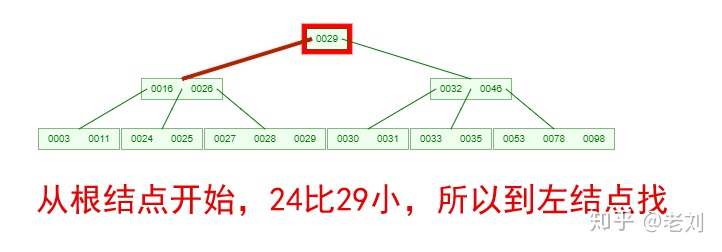
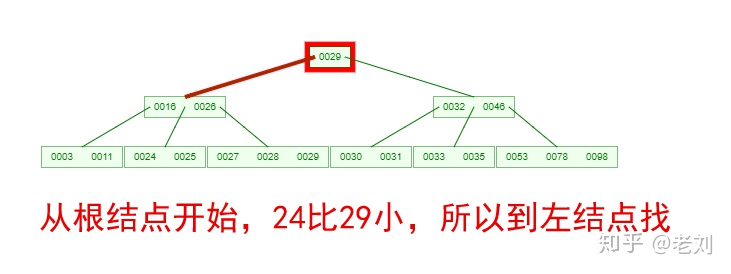
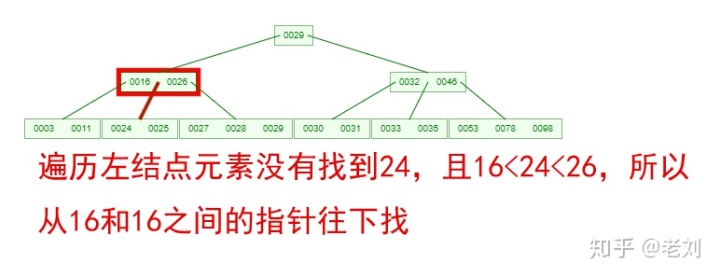
從這個流程我們能看出，B-Tree的查詢效率好像也并不比平衡二叉樹高。但是查詢所經過的結點數量要少很多，也就意味著要少很多次的磁盤IO，這對
性能的提升是很大的。

前面對B-Tree操作的圖我們能看出來，元素就是類似1、2、3這樣的數值，但是數據庫的數據都是一條條的數據，如果某個數據庫以B-Tree的數據結構存儲數據，那數據怎么存放的呢？我們看下一張圖：

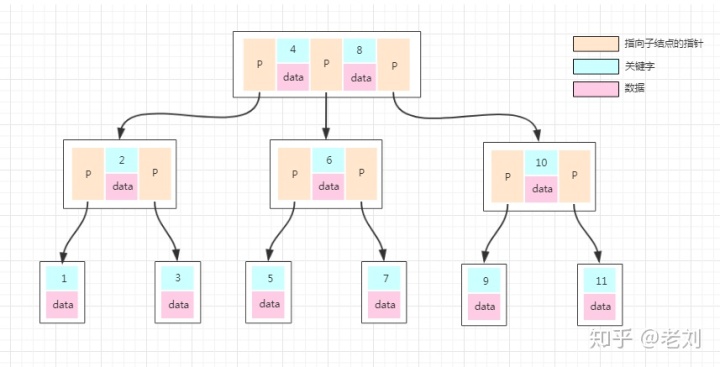
普通的B-Tree的結點中，元素就是一個個的數字。但是上圖中，我們把元素部分拆分成了key-data的形式，key就是數據的主鍵，data就是具體的數據。這樣我們在找一條數的時候，就沿著根結點往下找就ok了，效率是比較高的。

B+Tree

B+Tree是在B-Tree基礎上的一種優化，使其更適合實現外存儲索引結構。B+Tree與B-Tree的結構很像，但是也有幾個自己的特性：

1、所有的非葉子節點只存儲關鍵字信息。
2、所有衛星數據（具體數據）都存在葉子結點中。
3、所有的葉子結點中包含了全部元素的信息。
4、所有葉子節點之間都有一個鏈指針。

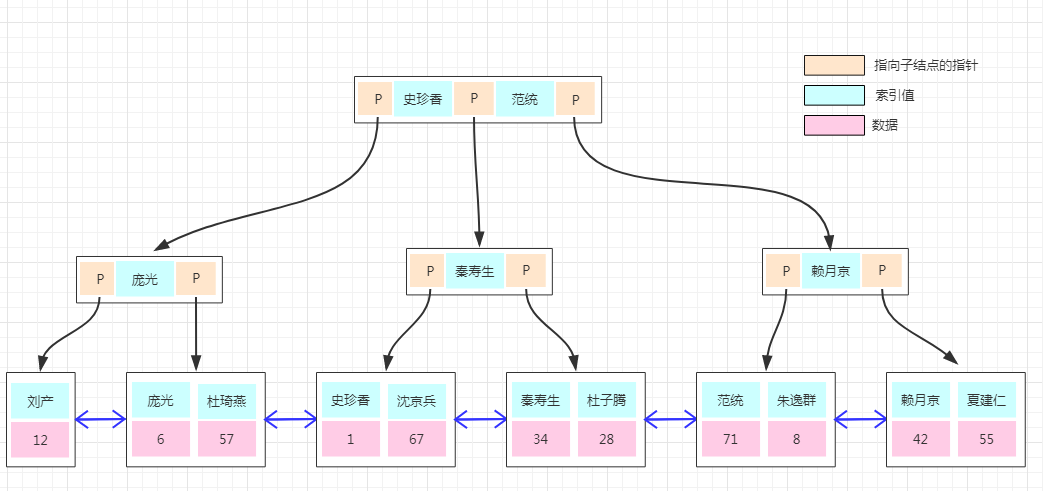
如果上面B-Tree的圖變成B+Tree，那應該如下：

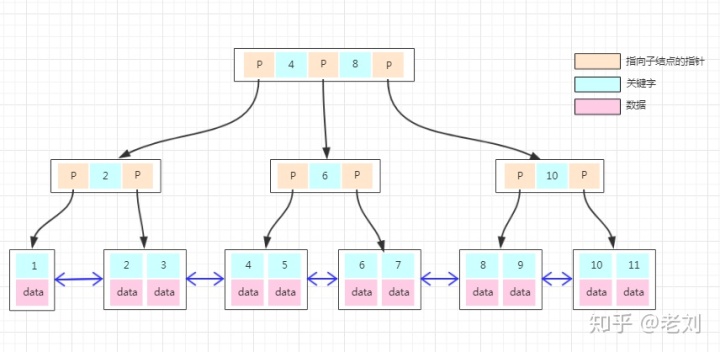
大家仔細對比于B-Tree的圖能發現什么不同？
1、非葉子結點上已經只有key信息了，滿足上面第1點特性！
2、所有葉子結點下面都有一個data區域，滿足上面第2點特性！
3、非葉子結點的數據在葉子結點上都能找到，如根結點的元素4、8在最底層的葉子結點上也能找到，滿足上面第3點特性！
4、注意圖中葉子結點之間的箭頭，滿足滿足上面第4點特性！

B-Tree or B+Tree？

在講這兩種數據結構在數據庫中的選擇之前，我們還需要了解的一個知識點是操作系統從磁盤讀取數據到內存是以磁盤塊（block）為基本單位的，位于同一個磁盤塊中的數據會被一次性讀取出來，而不是需要什么取什么。即使只需要一個字節，磁盤也會從這個位置開始，順序向后讀取一定長度的數據放入內存。這樣做的理論依據是計算機科學中著名的局部性原理：當一個數據被用到時，其附近的數據也通常會馬上被使用。
預讀的長度一般為頁（page）的整倍數。頁是計算機管理存儲器的邏輯塊，硬件及操作系統往往將主存和磁盤存儲區分割為連續的大小相等的塊，每個存儲塊稱為一頁（在許多操作系統中，頁得大小通常為4k）。

B-Tree和B+Tree該如何選擇呢？都有哪些優劣呢？
1、B-Tree因為非葉子結點也保存具體數據，所以在查找某個關鍵字的時候找到即可返回。而B+Tree所有的數據都在葉子結點，每次查找都得到葉子結點。所以在同樣高度的B-Tree和B+Tree中，B-Tree查找某個關鍵字的效率更高。
2、由于B+Tree所有的數據都在葉子結點，并且結點之間有指針連接，在找大于某個關鍵字或者小于某個關鍵字的數據的時候，B+Tree只需要找到該關鍵字然后沿著鏈表遍歷就可以了，而B-Tree還需要遍歷該關鍵字結點的根結點去搜索。
3、由于B-Tree的每個結點（這里的結點可以理解為一個數據頁）都存儲主鍵+實際數據，而B+Tree非葉子結點只存儲關鍵字信息，而每個頁的大小有限是有限的，所以同一頁能存儲的B-Tree的數據會比B+Tree存儲的更少。這樣同樣總量的數據，B-Tree的深度會更大，增大查詢時的磁盤I/O次數，進而影響查詢效率。
鑒于以上的比較，所以在常用的關系型數據庫中，都是選擇B+Tree的數據結構來存儲數據！下面我們以mysql的innodb存儲引擎為例講解，其他類似sqlserver、oracle的原理類似！

innodb引擎數據存儲

在InnoDB存儲引擎中，也有頁的概念，默認每個頁的大小為16K，也就是每次讀取數據時都是讀取4*4k的大小！假設我們現在有一個用戶表，我們往里面寫數據

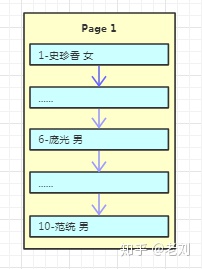
這里需要注意的一點是，在某個頁內插入新行時，為了不減少數據的移動，通常是插入到當前行的后面或者是已刪除行留下來的空間，所以在某一個頁內的數據并不是完全有序的（后面頁結構部分有細講），但是為了為了數據訪問順序性，在每個記錄中都有一個指向下一條記錄的指針，以此構成了一條單向有序鏈表，不過在這里為了方便演示我是按順序排列的！

由于數據還比較少，一個頁就能容下，所以只有一個根結點，主鍵和數據也都是保存在根結點（左邊的數字代表主鍵，右邊名字、性別代表具體的數據）。假設我們寫入10條數據之后，Page1滿了，再寫入新的數據會怎么存放呢？我們繼續看下圖：

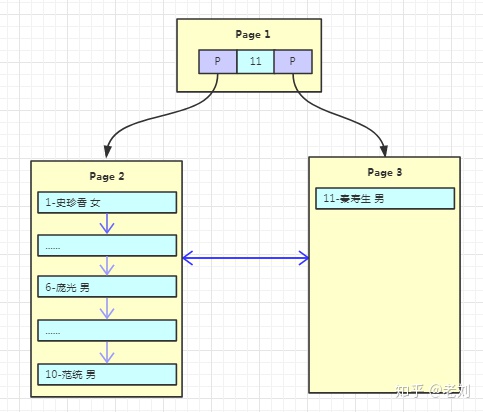
有個叫“秦壽生”的朋友來了，但是Page1已經放不下數據了，這時候就需要進行頁分裂，產生一個新的Page。在innodb中的流程是怎么樣的呢？

1、產生新的Page2，然后將Page1的內容復制到Page2。
2、產生新的Page3，“秦壽生”的數據放入Page3。
3、原來的Page1依然作為根結點，但是變成了一個不存放數據只存放索引的頁，并且有兩個子結點Page2、Page3。

這里有兩個問題需要注意的是
1、為什么要復制Page1為Page2而不是創建一個新的頁作為根結點，這樣就少了一步復制的開銷了？
如果是重新創建根結點，那根結點存儲的物理地址可能經常會變，不利于查找。并且在innodb中根結點是會預讀到內存中的，所以結點的物理地址固定會比較好！

2、原來Page1有10條數據，在插入第11條數據的時候進行裂變，根據前面對B-Tree、B+Tree特性的了解，那這至少是一顆11階的樹，裂變之后每個結點的元素至少為11/2=5個，那是不是應該頁裂變之后主鍵1-5的數據還是在原來的頁，主鍵6-11的數據會放到新的頁，根結點存放主鍵6？
如果是這樣的話新的頁空間利用率只有50%，并且會導致更為頻繁的頁分裂。所以innodb對這一點做了優化，新的數據放入新創建的頁，不移動原有頁面的任何記錄。

隨著數據的不斷寫入，這棵樹也逐漸枝繁葉茂，如下圖：

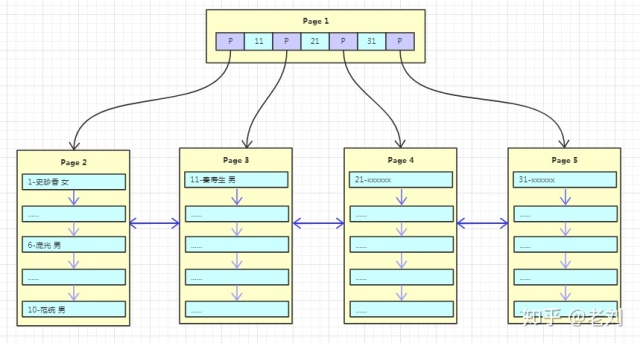
每次新增數據，都是將一個頁寫滿，然后新創建一個頁繼續寫，這里其實是有個隱含條件的，那就是主鍵自增！主鍵自增寫入時新插入的數據不會影響到原有頁，插入效率高！且頁的利用率高！但是如果主鍵是無序的或者隨機的，那每次的插入可能會導致原有頁頻繁的分裂，影響插入效率！降低頁的利用率！這也是為什么在innodb中建議設置主鍵自增的原因！

這棵樹的非葉子結點上存的都是主鍵，那如果一個表沒有主鍵會怎么樣？在innodb中，如果一個表沒有主鍵，那默認會找建了唯一索引的列，如果也沒有，則會生成一個隱形的字段作為主鍵！

有數據插入那就有刪除，如果這個用戶表頻繁的插入和刪除，那會導致數據頁產生碎片，頁的空間利用率低，還會導致樹變的“虛高”，降低查詢效率！這可以通過索引重建來消除碎片提高查詢效率！

innodb引擎數據查找

數據插入了怎么查找呢？

1、找到數據所在的頁。這個查找過程就跟前面說到的B+Tree的搜索過程是一樣的，從根結點開始查找一直到葉子結點。
2、在頁內找具體的數據。讀取第1步找到的葉子結點數據到內存中，然后通過分塊查找的方法找到具體的數據。

這跟我們在新華字典中找某個漢字是一樣的，先通過字典的索引定位到該漢字拼音所在的頁，然后到指定的頁找到具體的漢字。innodb中定位到頁后用了哪種策略快速查找某個主鍵呢？這我們就需要從頁結構開始了解。

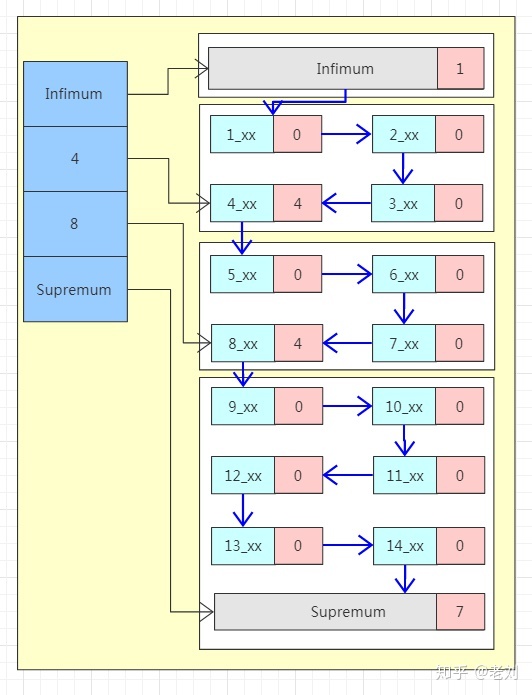
左邊藍色區域稱為Page Directory，這塊區域由多個slot組成，是一個稀疏索引結構，即一個槽中可能屬于多個記錄，最少屬于4條記錄，最多屬于8條記錄。槽內的數據是有序存放的，所以當我們尋找一條數據的時候可以先在槽中通過二分法查找到一個大致的位置。

右邊區域為數據區域，每一個數據頁中都包含多條行數據。注意看圖中最上面和最下面的兩條特殊的行記錄Infimum和Supremum，這是兩個虛擬的行記錄。在沒有其他用戶數據的時候Infimum的下一條記錄的指針指向Supremum，當有用戶數據的時候，Infimum的下一條記錄的指針指向當前頁中最小的用戶記錄，當前頁中最大的用戶記錄的下一條記錄的指針指向Supremum，至此整個頁內的所有行記錄形成一個單向鏈表。

行記錄被Page Directory邏輯的分成了多個塊，塊與塊之間是有序的，也就是說“4”這個槽指向的數據塊內最大的行記錄的主鍵都要比“8”這個槽指向的數據塊內最小的行記錄的主鍵要小。但是塊內部的行記錄不一定有序。

每個行記錄的都有一個n_owned的區域（圖中粉紅色區域），n_owned標識這個這個塊有多少條數據，偽記錄Infimum的n_owned值總是1，記錄Supremum的n_owned的取值范圍為[1,8]，其他用戶記錄n_owned的取值范圍[4,8]，并且只有每個塊中最大的那條記錄的n_owned才會有值，其他的用戶記錄的n_owned為0。

所以當我們要找主鍵為6的記錄時，先通過二分法在稀疏索引中找到對應的槽，也就是Page Directory中“8”這個槽，“8”這個槽指向的是該數據塊中最大的記錄，而數據是單向鏈表結構所以無法逆向查找，所以需要找到上一個槽即“4”這個槽，然后通過“4”這個槽中最大的用戶記錄的指針沿著鏈表順序查找到目標記錄。

聚集索引&非聚集索引

前面關于數據存儲的都是演示的聚集索引的實現，如果上面的用戶表需要以“用戶名字”建立一個非聚集索引，是怎么實現的呢？我們看下圖：

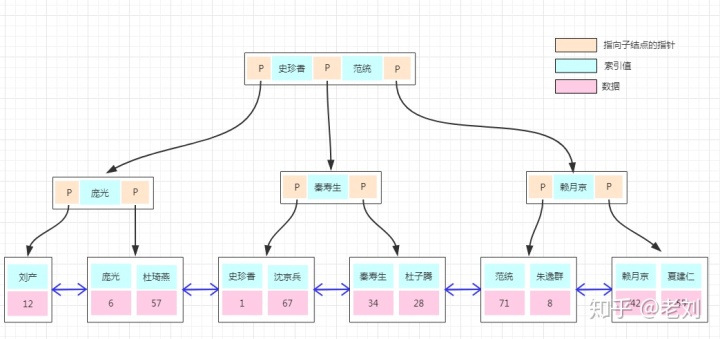
非聚集索引的存儲結構與前面是一樣的，不同的是在葉子結點的數據部分存的不再是具體的數據，而數據的聚集索引的key。所以通過非聚集索引查找的過程是先找到該索引key對應的聚集索引的key，然后再拿聚集索引的key到主鍵索引樹上查找對應的數據，這個過程稱為回表！

圖中的這些名字均來源于網絡，希望沒有誤傷正在看這篇文章的你~^_^

innodb與MyISAM兩種存儲引擎對比

上面包括存儲和搜索都是拿的innodb引擎為例，那MyISAM與innodb在存儲上有啥不同呢？憋縮話，看圖：

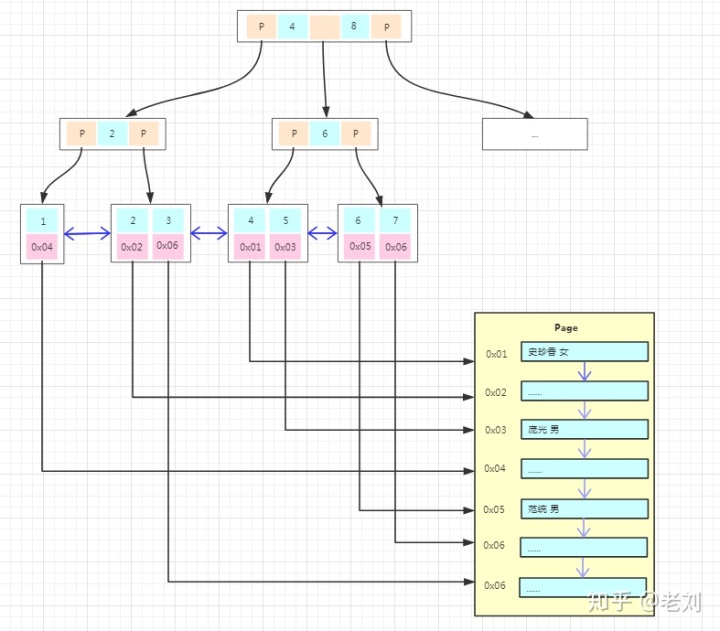
上圖為MyISAM主鍵索引的存儲結構，我們能看到的不同是

1、主鍵索引樹的葉子結點的數據區域沒有存放實際的數據，存放的是數據記錄的地址。
2、數據的存儲不是按主鍵順序存放的，按寫入的順序存放。

也就是說innodb引擎數據在物理上是按主鍵順序存放，而MyISAM引擎數據在物理上按插入的順序存放。并且MyISAM的葉子結點不存放數據，所以非聚集索引的存儲結構與聚集索引類似，在使用非聚集索引查找數據的時候通過非聚集索引樹就能直接找到數據的地址了，不需要回表，這比innodb的搜索效率會更高呢！