圖像處理核函數:之高斯核函數的生成方法 python
- 高斯核函數(低通高斯濾波器核)
- 高斯分布函數
- 高斯核生成函數
- 代碼
- 效果
- 高斯核函數的圖像
高斯核函數(低通高斯濾波器核)
最近在看DIP(Digital Image Processing),雖然可以調用Opencv的函數,但還是被這高斯核函數所吸引,這可能也是高斯分態對我的吸引力。
高斯分布函數
G(x)=12πσe?(x?x0)22σ2G(x) = \frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{(x-x_0)^2}{2\sigma^2}}G(x)=2πσ?1?e?2σ2(x?x0?)2?
這是我們常見的高斯分布概率密度函數(正態分布)
高斯核生成函數
DIP書上給出的高斯核函數
G(s,t)=Ke?s2+t22σ2G(s, t) = K e^{-\frac{s^2 + t^2}{2\sigma^2}}G(s,t)=Ke?2σ2s2+t2?
看起來跟高斯分布是不是有點相似,但卻有點不同,其實沒有關系的。這里的K可以看成是歸一化因子,而重要是的e?s2+t22σ2e^{-\frac{s^2 + t^2}{2\sigma^2}}e?2σ2s2+t2?這部分。
好了,有了函數,我們就可以寫代碼了。
代碼
下面公式是我生成高期核的用到的公式:
G(x,y)=12πσ2e?(x?x0)2+(y?y0)22σ2G(x, y) = \frac {1} {2\pi\sigma ^2}e^{-\frac{(x-x_0)^2+(y-y_0)^2}{2\sigma^2}}G(x,y)=2πσ21?e?2σ2(x?x0?)2+(y?y0?)2?
# 高斯核生成函數
def creat_gauss_kernel(kernel_size=3, sigma=1, k=1):if sigma == 0:sigma = ((kernel_size - 1) * 0.5 - 1) * 0.3 + 0.8X = np.linspace(-k, k, kernel_size)Y = np.linspace(-k, k, kernel_size)x, y = np.meshgrid(X, Y)x0 = 0y0 = 0gauss = 1/(2*np.pi*sigma**2) * np.exp(- ((x -x0)**2 + (y - y0)**2)/ (2 * sigma**2))return gauss
默認參數生成的高斯核:
[0.05854983, 0.09653235, 0.05854983],
[0.09653235, 0.15915494, 0.09653235],
[0.05854983, 0.09653235, 0.05854983]
- 為什么要判斷sigma是否為0?
- k是什么,對核函數有何影響,對最終的圖像有何影響?
- 代碼有核的大小
- 代碼有可定義的σ\sigmaσ
效果
左邊是默認的3X3 高斯核,右邊是自己生成的3X3的高斯核,從效果來看,沒有什么差別,這也說明生成的高斯核可用。
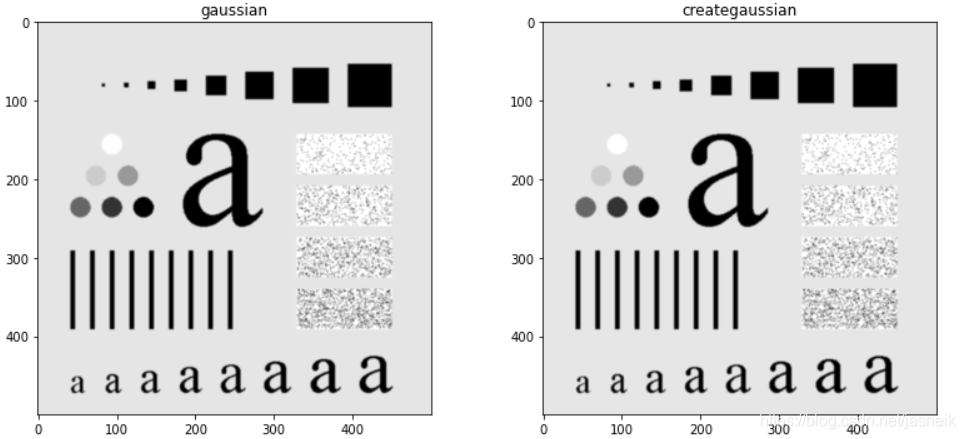
高斯核函數的圖像
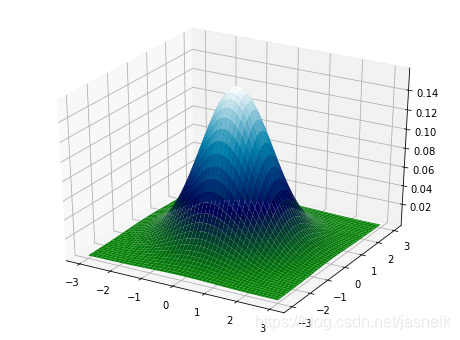







方法的使用)

, Keras實現,模型優化)




 --數字圖像基礎1 - 視覺感知要素 - 亮度適應與辨別)



 --緒論)
