遞歸函數（一）：開篇
遞歸函數（二）：編寫遞歸函數的思路和技巧
遞歸函數（三）：歸納原理
遞歸函數（四）：全函數與計算的可終止性
遞歸函數（五）：遞歸集與遞歸可枚舉集
遞歸函數（六）：最多有多少個程序
遞歸函數（七）：不動點算子
遞歸函數（八）：偏序結構
遞歸函數（九）：最小不動點定理

• • -

回顧

上文我們討論了集合上的偏序結構，之所以談論它們是因為，
完全偏序集上的連續函數具有最小不動點，這稱之為最小不動點定理，
除了集合論的一些知識之外，我們還要討論到底什么是連續函數，以及什么是完全偏序集。

有向子集與完全偏序

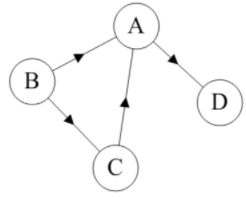
偏序集\((D,leqslant )\)的非空子集\(Ssubseteq D\)叫做有向子集（directed subset），
當且僅當，對于\(S\)中的任意元素\(a,bin S\)，
存在\(S\)中的一個元素\(c\)，有\(aleqslant c\)且\(bleqslant c\)。

如果一個偏序集\((D,leqslant )\)的每個有向子集\(Ssubseteq D\)都有上確界（記為\(bigvee S\)）
就稱它是一個有向完全偏序集，
此外，如果它還有最小元，就稱它是一個完全偏序集。

注意，完全偏序集并不是每一個子集都有上確界，
而是它的每一個有向子集都有上確界。

連續函數

假設\((D,leqslant )\)與\((E,leqslant )\)是完全偏序集，
\(f:Drightarrow E\)是集合上定義的一個函數，
如果，\(Ssubseteq D\)，則\(f(S)\)為\(E\)的子集，
其中\(f(S)=lbrace f(d)| din S rbrace\)。

對于任意的\(d,d'in D\)，如果\(dleqslant d'\)就有\(f(d)leqslant f(d')\)，
我們就說\(f\)是單調的。
可以看出，如果\(f\)是單調的，且\(S\)是\(D\)的有向子集，那么\(f(S)\)也是\(E\)的有向子集。

如果\(f\)是單調的，且對于任意有向子集\(Ssubseteq D\)，
有\(f(bigvee S)=bigvee f(S)\)，就稱\(f\)是連續的。

連續函數集上的偏序結構

完全偏序集\((D,leqslant )\)和\((E,leqslant )\)上的連續也可以定義偏序結構，
我們稱\(fleqslant g\)，當且僅當對于每一個\(din D\)，我們有\(f(d)leqslant g(d)\)。
這樣我們就得到了一個元素為連續函數的偏序集，\((Drightarrow E,leqslant )\)。
可以證明，\((Drightarrow E,leqslant )\)也是一個完全偏序集。（證略

最小不動點定理

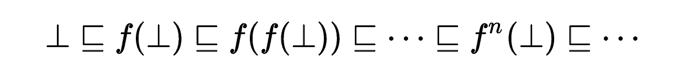
如果\((D,leqslant )\)是一個完全偏序集，且\(f:Drightarrow D\)是連續的，
則\(f\)有最小不動點，\(fix_D f=bigvee lbrace f^n(perp )| ngeqslant 0 rbrace \)。

因為\(perp \)是\(D\)中的最小元，且\(f(perp )in D\)，所以，\(perp leqslant f(perp )\)，
因為\(f\)是連續的，所以\(f\)也一定是單調的，所以，\(f(perp )leqslant f^2(perp )\)，
繼而，\(f^n(perp )leqslant f^{n+1}(perp )\)，對于任意的\(ngeqslant 0\)都成立。

\(lbrace f^n(perp )| ngeqslant 0 rbrace\)構成了一個全序集，
所以，它是完全偏序集\((Drightarrow E,leqslant)\)的一個有向子集，必有上確界。

設\(a\)是上確界，\(a=bigvee lbrace f^n(perp )| ngeqslant 0 rbrace \)，
首先\(a\)是\(f\)的不動點，因為，由\(f\)的連續性，
\(f(a)=f(bigvee lbrace f^n(perp )| ngeqslant 0 rbrace )\)
\(f(a)=bigvee lbrace f^{(n+1)}(perp )| ngeqslant 0 rbrace \)，
但是由于\(lbrace f^n(perp ) rbrace\)與\(lbrace f^{(n+1)}(perp ) rbrace\)，有同樣的上確界，
所以，\(f(a)=a\)。

其次，\(a\)是\(f\)的最小不動點，
假設\(b=f(b)\)是\(f\)的任意不動點，因為\(perp leqslant b\)，所以\(f(perp )leqslant f(b)\)，
類似的，對于任意的\(ngeqslant 0\)，\(f^n(perp )leqslant f^n(b)\)。
但是，由于\(b\)是\(f\)的不動點，所以\(f^n(b)=b\)，
因此\(b\)是集合\(lbrace f^n(perp )| ngeqslant 0 rbrace\)的上界。
由于集合的最小上界是\(a\)，所以有\(aleqslant b\)。

后繼函數的不動點

succ :: Int -> Int
succ n = n+1

在第七篇中，我們說fix可以得到任意函數的不動點，
那么這個succ函數呢？它有沒有不動點？
fix succ是什么？

現在我們有了最小不動點定理，
就得驗證succ所指稱的數學函數，是不是一個完全偏序集上的連續函數，
如果是的話，它就有不動點。

在第四篇為了表示計算的不可終止性，我們對自然數集進行了擴充，\(Ncup lbrace perp rbrace\)，
然后用這個集合作為程序中Int類型的值的解釋。

然而，\(Ncup lbrace perp rbrace\)不是一個完全偏序集，原因是它沒有上界，
如果我們額外加入一個比其他的自然都大的元素\(+infty \)，
則我們就得到了一個完全偏序集，\(Ncup lbrace perp rbracecup lbrace +infty rbrace\)。

然后，我們看succ連續嗎？
首先，它是單調的，如果我們再定義\(succ(+infty )=+infty \)，
就有\(succ(bigvee N)=bigvee succ(N)\)，
因此，succ是一個連續函數。

根據最小不動點定理，succ的最小不動點是，\(fix succ=bigvee lbrace succ^n(perp )| ngeqslant 0 rbrace \)。

由于\(succ(perp )=perp \)，即對于非終止的輸入succ的計算也不會終止，
所以\(succ^n(perp )=perp \)，
因此，\(fix succ=bigvee lbrace succ^n(perp )| ngeqslant 0 rbrace =perp \)，
即，succ的最小不動點是\(perp \)，fix succ的計算不會終止。

求解階乘函數

上一篇中，我們證明了階乘函數fact是以下函數的不動點，fact = fix g，

g :: (Int -> Int) -> Int -> Int
g f n = case n of1 -> 1_ -> n * f (n-1)

現在我們來看一下，如何運用最小不動點定理來得到這個答案。
為了避免篇幅過長，關于g函數的連續性證明暫略，
我們直接使用公式，
\(fix g=bigvee lbrace g^n(perp )| ngeqslant 0 rbrace \)，
即，g函數的最小不動點，就是集合\(D=lbrace g^n(perp )| ngeqslant 0 rbrace\)的上確界。

我們先來看一下這個集合\(D\)中有哪些元素，
其中，\(g(perp )in D\)，我們將\(perp \)傳入\(g\)中，看看會得到什么，

f1 = \n -> case n of1 -> 1_ -> ...

這個函數能計算f1 1，但是不能計算f1 2，恰好是fact函數有限展開的一階項。

我們再來看\(g^2(perp )in D\)，它等于\(g(f1)\)，

f2 = \n -> case n of1 -> 1_ -> n * f1 (n-1)

這個函數能計算f2 1以及f2 2，但是不能計算f2 3，恰好是fact函數展開的二階項。

由此，我們看出了規律，
\(g^n(perp )in D\)就是fact函數有限展開的第\(n\)階項。
上一篇中，我們已經證明了，當\(nrightarrow infty\)時，它就是fact函數，
考慮到\(f1,f2,cdots\)這些函數的序關系，
因此，我們有\(fact=bigvee lbrace g^n(perp )| ngeqslant 0 rbrace \)。

即，fact函數就是g函數的最小不動點。

總結

到此為止，我想這個系列的文章已經討論完了，
本系列文章一直圍繞著遞歸函數和不動點進行分析，
在內容上可以分為兩個部分，前半部分主要與可計算性理論有關，
后半部分與不動點定理有關，希望對大家有所幫助。

參考

有向集合
完全偏序
Kleene fixed-point theorem
Foundations for Programming Languages