Factorial Trailing Zeroes

https://leetcode.com/problems/factorial-trailing-zeroes/

Given an integer?n, return the number of trailing zeroes in?n!.

Note:?Your solution should be in logarithmic time complexity.

解題思路：

再次遇見最討厭的Math題。

開始的思路，結尾的0到底是哪來的？要有0，必須要乘積為10，那么可能2*5或者1*10，那么10又是2*5，所以就是去算有多少對2和5？再去看百度百科上20以內的階乘?http://baike.baidu.com/view/245476.htm ，似乎也驗證了有多少個5就有多少個0。因為2肯定比5多。

于是寫下來下面的代碼，該不會這么簡單吧。

public class Solution {public int trailingZeroes(int n) {return n / 5;}
}

果然錯了。想不出來，只能去求助網友。

后來看見了Wikipedia-Trailing Zeroes，

The number of trailing zeros in the?decimal representation?of?n!, the?factorial?of a?non-negative?integer?n, is simply the multiplicity of the?primefactor?5 in?n!. This can be determined with this special case of?de Polignac's formula:^[1]

where?k?must be chosen such that

and?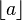?denotes the?floor function?applied to?a. For?n?=?0,?1,?2,?... this is

0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 6, ... (sequence?A027868?in?OEIS).

For example, 5³?>?32, and therefore?32!?=?263130836933693530167218012160000000 ends in

zeros. If?n?<?5, the inequality is satisfied by?k?=?0; in that case the sum is?empty, giving the answer?0.

也就是說，n!的結尾0的數量就等于n/5+n/25+n/125...

不過為什么除以5以后還要再除以25，除以125？顯然因為25里有2個5，125里有3個5。但是為什么不是n/5+2*n/25+3*n/125...？因為n/5里面已經包含了25里的一個5了，同樣n/25也包含了n/125里的一個5了。

于是寫了以下代碼

public class Solution {public int trailingZeroes(int n) {int base = 5, result = 0;;while(base <= n){result += n / base;base *= 5;}return result;}
}

n=2147483647的時候，居然超時。原來是base*5到僅僅小于Integer.MAX_VALUE的時候，就超時了。

偷懶的將base申明為long，算是解決了。

public class Solution {public int trailingZeroes(int n) {long base = 5;int result = 0;while(base <= n){result += n / base;base *= 5;}return result;}
}

其實n/base，base *= 5，不就是n/base，n /= 5嗎？這樣做更好點。

public class Solution {public int trailingZeroes(int n) {long base = 5;int result = 0;while(base <= n){result += n / base;n /= 5;}return result;}
}

數學題真是弱啊，要重視。