數據結構（復習）--------關于平衡二叉樹（轉載）

在上一個專題中，我們在談論二叉查找樹的效率的時候。不同結構的二叉查找樹，查找效率有很大的不同（單支樹結構的查找效率退化成了順序查找）。如何解決這個問題呢？關鍵在于如何最大限度的減小樹的深度。正是基于這個想法，平衡二叉樹出現了。

?

平衡二叉樹的定義 （AVL—— 發明者為Adel'son-Vel'skii 和 Landis）

?

平衡二叉查找樹，又稱 AVL樹。 它除了具備二叉查找樹的基本特征之外，還具有一個非常重要的特點：它 的左子樹和右子樹都是平衡二叉樹，且左子樹和右子樹的深度之差的絕對值（平衡因子 ） 不超過1。 也就是說AVL樹每個節點的平衡因子只可能是-1、0和1（左子樹高度減去右子樹高度）。

?

那么如何是二叉查找樹在添加數據的同時保持平衡呢？基本思想就是：當在二叉排序樹中插入一個節點時，首先檢查是否因插入而破壞了平衡，若 破壞，則找出其中的最小不平衡二叉樹，在保持二叉排序樹特性的情況下，調整最小不平衡子樹中節點之間的關系，以達 到新的平衡。所謂最小不平衡子樹 指離插入節點最近且以平衡因子的絕對值大于1的節點作為根的子樹。

?

平衡二叉樹的操作

?

1. 查找操作

?????? 平衡二叉樹的查找基本與二叉查找樹相同。

?

2. 插入操作

?????? 在平衡二叉樹中插入結點與二叉查找樹最大的不同在于要隨時保證插入后整棵二叉樹是平衡的。那么調整不平衡樹的基本方法就是： 旋轉 。 下面我們歸納一下平衡旋轉的4中情況

1) 繞某元素左旋轉 ?

???????????????????????????????? 80 ? ? ? ? ?? ??????????????????????? 90 ?

? ? ? ? ???????????????????????? /? \???????????? 左旋 ????????????? / ?? \

?????????????????????????????? 60?90?????? ?? ---- ->? ? ? ?? 80???? 120

??????????????????????????????????? /? \??????????????????? ? ?? ?? ?? /? \?????? /

????????????????????????????????? 85?120??????????????????? 60? 85 100

??????????????????????????????????????? /

????????????????????????????????????? 100?????

?????????????????????????????? a)? BST樹????????????????????????????? b ) AVL樹

???? 分析一下：在插入數據100之前，a圖的B ST樹只有80節點的平衡因子是-1(左高-右高)，但整棵樹還是平衡的。加入100之后，80節點的平衡因子就成為了-2，此時平衡被破壞。需要左旋轉成b 圖。

???? 當樹中節點X的右孩子的右孩子上插入新元素，且平衡因子從-1變成-2后，就需要繞節點X進行左旋轉。

?

2) 繞某元素右旋轉 ?

??????????????????????????????? 100?????????????????????????????????? 85

???????????????????????????????? /? \?????????????? 右旋 ???????????? /??? \

????????????????????????????? 85? 120???????? ------ -> ? ? 60??? 100 ?

????????????????????????????? /? \?????????????????????????????????? ?? \ ? ?? / ? \

??????????????????????????? 60?90????????????????????????????? ?? 80? 90?120

????????????????????????????? \

????????????????????????????? 80

????????????????????????? ?? a) B ST樹??????????????????????????????? b) AVL樹

???? 當樹中節點X的左孩子的左孩子上插入新元素，且平衡因子從1變成2后，就需要繞節點X進行右旋轉。

?

3) 繞某元素的左子節點左旋轉，接著再繞該元素自己右旋轉。 此情況下就是左旋與右旋?的結合，具體操作時可以分 解成這兩種操作，只是圍繞點不一樣而已。

???? ? ? ? ? ? ? ?? ??????????????????????????????????

??????????????????????????? 100???????????????????????????? 100 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? 90

???????????????????????????? /? \???????????? 左旋 ?????? ? ? /? \????????????? 右旋 ????? ? ? / ?? \

????????????????????????? 80? 120?????? ------> ? ?? 90? 120??????? ------> ? ? 80?? 100 ?

????????????????????????? / \?????????????????????????????? ?? /?????????????????????? ? ?????? ? ? /? \????? \

?????????????????????? 60?90 ? ? ? ? ? ? ? ? ? ???????? 80??????????????? ? ? ? ????? ? 60? 85? 120

??????????????????????????? /?????????????????????????????? / \

????????????????????????? 85??????????????????????????? 60?85

????? 當樹中節點X的左孩子的右孩子上插入新元素，且 平衡因子從1變成2后，就需要 先繞X的左子節點Y左旋轉，接著再繞X右旋轉

4) 繞某元素的右子節點右旋轉，接著再繞該元素自己左旋轉。 此情況下就是?右旋與左旋?的結合，具體操作時可以分解 成這兩種操作，只是圍繞點不一樣而已 。

?

?????????????????????????????? 80?????????????????????????????? 80 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ? ? 85 ?

?????????????????????????????? / ? \???????????? 右 旋 ? ? ?? ? /? \?????????? ????? 左 旋 ??????????? /? \ ????

??????????????????????????? 60? 100 ? ?? ------> ???? 60?85 ? ? ? ? ?? -------> ? ?????? 80?100

?????????????????????????????????? /? \??????????????? ? ? ? ? ? ? ? ?? \?????????????????????????? ? ? ? ? /???? /?? \ ??????

? ? ? ? ??????????????????????? 85? 120??????????????????????? 100?????????????????????? ? ? 60??? 90?120

???????????????????????????????? ? \?????????????????????????????? ? ? /? \

?????????????????????????????????? 90???????????????????????? ? 90? 120

?????? 當樹中節點X的右孩子的左孩子上插入新元素，且 平衡因子從-1變成-2后，就需要 先繞X的右子節點Y右旋轉，接著再繞X左旋轉

?

?

平衡二叉樹性能分析

平衡二叉樹的性能優勢：

????? 很顯然，平衡二叉樹的優勢在于不會出現普通二叉查找樹的最差情況。其查找的時間復雜度為O(logN)。

?

平衡二叉樹的缺陷：

????? (1) 很遺憾的是，為了保證高度平衡，動態插入和刪除的代價也隨之增加。因此，我們在下一專題中講講《紅黑樹》 這種更加高效的查找結構。

?

??? ? (2) 所有二叉查找樹結構的查找代價都與樹高是緊密相關的，能否通過減少樹高來進一步降低查找代價呢。我們可以通過多路查找樹的結構來做到這一點，在后面專題中我們將通過《多路查找樹/B-樹/B+樹 》來介紹。

?

????? (3) 在大數據量查找環境下(比如說系統磁盤里的文件目錄，數據庫中的記錄查詢 等)，所有的二叉查找樹結構(BST、AVL、RBT)都不合適。如此大規模的數據量（幾G數據），全部組織成平衡二叉樹放在內存中是不可能做到的。那么 把這棵樹放在磁盤中吧。問題就來了：假如構造的平衡二叉樹深度有1W層。那么從根節點出發到葉子節點很可能就需要1W次的硬盤IO讀寫。大家都知道，硬盤的機械部件讀寫數據的速度遠遠趕不上純電子媒體的內存。 查找效率在IO讀寫過程中將會付出巨大的代價。在大規模數據查詢這樣一個實際應用背景下，平衡二叉樹的效率就很成問題了。對這一問題的解決：我們也會在《多路查找樹/B-樹/B+樹 》 將詳細分析。

?

????? 上面提到的紅黑樹和多路查找樹都是屬于深度有界查找樹（depth-bounded tree —DBT）

?

來自于：http://hxraid.iteye.com/blog/609949

----------------------------------------------------------------------------------------------------------------------------------------------------------

typedef?int?ElementType;??
??
#ifndef?AVLTREE_H??
#define?AVLTREE_H??
??
struct?TreeNode??
{??
????ElementType?Element;??
????int?Height;??
????struct?TreeNode?*Left;??
????struct?TreeNode?*Right;??
};??
??
typedef?struct?TreeNode?*AvlTree;??
typedef?struct?TreeNode?*Position;??
??
AvlTree?MakeEmpty(AvlTree?T);??
AvlTree?Insert(ElementType?X,?AvlTree?T);??
Position?Find(ElementType?X?,AvlTree?T);??
Position?FindMax(AvlTree?T);??
Position?FindMin(AvlTree?T);??
??
#endif??

avltree.c函數實現

#include?"fatal.h"??
#include?"avltree.h"??
??
AvlTree?MakeEmpty(AvlTree?T)??
{??
????if(T?!=?NULL)??
????{??
????????MakeEmpty(T->Left);??
????????MakeEmpty(T->Right);??
????????free(T);??
????}??
????return?NULL;??
}??
??
static?int?Height(Position?P)??
{??
????if(P?==?NULL)??
????????return?-1;??
????else??
????????return?P->Height;??
}??
??
static?int?Max(int?Lhs,?int?Rhs)??
{??
????return?Lhs?>?Rhs???Lhs?:?Rhs;??
}??
??
static?Position?SingleRotateWithLeft(Position?K2)??
{??
????Position?K1;??
??
????K1?=?K2->Left;??
????K2->Left?=?K1->Right;??
????K1->Right?=?K2;??
??
????K1->Height?=?Max(Height(K1->Left),?Height(K1->Right))?+?1;??
????K2->Height?=?Max(Height(K2->Left),?Height(K2->Right))?+?1;??
??
????return?K1;??
}??
??
static?Position?SingleRotateWithRight(Position?K2)??
{??
????Position?K1;??
??
????K1?=?K2->Right;??
????K2->Right?=?K1->Left;??
????K1->Left?=?K2;??
??
????K1->Height?=?Max(Height(K1->Left),?Height(K1->Right))?+?1;??
????K2->Height?=?Max(Height(K2->Left),?Height(K2->Right))?+?1;??
??
????return?K1;??
}??
??
static?Position?DoubleRotateWithLeft(Position?K3)??
{??
????K3->Left?=?SingleRotateWithRight(K3->Left);??
????return?SingleRotateWithLeft(K3);??
}??
??
static?Position?DoubleRotateWithRight(Position?K3)??
{??
????K3->Right?=?SingleRotateWithLeft(K3->Right);??
????return?SingleRotateWithRight(K3);??
}??
??
AvlTree?Insert(ElementType?X,?AvlTree?T)??
{??
????if(T?==?NULL)??
????{??
????????T?=?(Position)malloc(sizeof(struct?TreeNode));??
????????if(T?==?NULL)??
????????????FatalError("Out?of?space");??
????????T->Element?=?X;??
????????T->Height?=?0;??
????????T->Left?=?T->Right?=?NULL;??
????}??
????else?if(X?<?T->Element)//左子樹插入新節點??
????{??
????????T->Left?=?Insert(X,?T->Left);??
????????if(Height(T->Left)?-?Height(T->Right)?==?2)//左子樹插入節點所以高度是左子樹高于右子樹??
????????{??
????????????if(X?<?T->Left->Element)//對α的左兒子的左子樹進行一次插入，需要左旋??
????????????????T?=?SingleRotateWithLeft(T);??
????????????else?//對α的左兒子的右子樹進行一次插入，需要雙旋??
????????????????T?=?DoubleRotateWithLeft(T);??
????????}??
????}??
????else?if(X?>?T->Element)//右子樹插入新節點??
????{??
????????T->Right?=?Insert(X,?T->Right);??
????????if(Height(T->Right)?-?Height(T->Left)?==?2)//因為是右子樹插入新節點，所以高度是右子樹高于左子樹??
????????{??
????????????if(X?>?T->Right->Element)//對α的右兒子的右子樹進行一次插入，需要右旋??
????????????????T?=?SingleRotateWithRight(T);??
????????????else//對α的右兒子的左子樹進行一次插入，需要雙旋??
????????????????T?=?DoubleRotateWithRight(T);??
????????}??
????}??
????T->Height?=?Max(Height(T->Left),?Height(T->Right))?+?1;??
????return?T;??
}??
??
Position?Find(ElementType?X,?AvlTree?T)??
{??
????if(T?==?NULL)??
????????return?NULL;??
????if(X?<?T->Element)??
????????return?Find(X,?T->Left);??
????else?if(X?>?T->Element)??
????????return?Find(X,?T->Right);??
????else??
????????return?T;??
}??
??
Position?FindMin(AvlTree?T)??
{??
????if(T?==?NULL)??
????????return?NULL;??
????else?if(T->Left?==?NULL)??
????????return?T;??
????else??
????????return?FindMin(T->Left);???
}??
??
Position?FindMax(AvlTree?T)??
{??
????if(T?==?NULL)??
????????return?NULL;??
????else?if(T->Right?==?NULL)??
????????return?T;??
????else??
????????return?FindMax(T->Right);??
}??

testavl.c測試AVL樹的實現

#include?"avltree.h"??
#include?<stdio.h>??
#include?<stdlib.h>??
??
void?InOrder(AvlTree?T)??
{??
????if(T?!=?NULL)??
????{??
????????InOrder(T->Left);??
????????printf("%d?",?T->Element);??
????????InOrder(T->Right);??
????}??
}??
??
void?PreOrder(AvlTree?T)??
{??
????if(T?!=?NULL)??
????{??
????????printf("%d?",?T->Element);??
????????PreOrder(T->Left);??
????????PreOrder(T->Right);??
????}??
}??
??
int?main(void)??
{??
????AvlTree?T;??
????Position?P;??
????int?i;??
??
????T?=?MakeEmpty(NULL);??
????for(i?=?1;?i?<=?7;?i++)??
????????T?=?Insert(i,?T);??
????for(i?=?16;?i?>=?10;?i--)??
????????T?=?Insert(i,?T);??
????T?=?Insert(8,?T);??
????T?=?Insert(9,?T);??
????printf("Root:?%d\n",?T->Element);??
????printf("InOrder:??");??
????InOrder(T);??
????printf("\nPreOrder:?");??
????PreOrder(T);??
????putchar('\n');??
????system("Pause");??
??
????return?0;??
}??

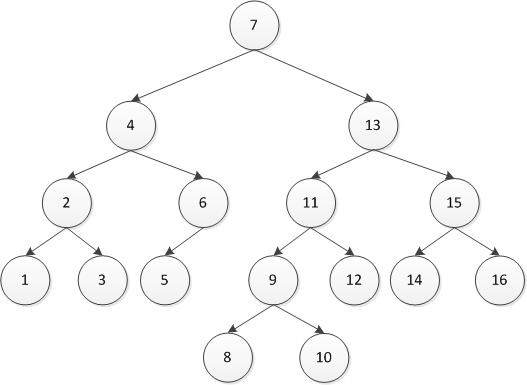
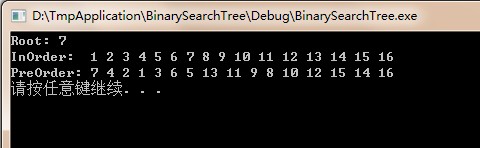
測試：首先插入1到7，然后插入16到10，最后插入8和9。AVL樹的應該為下圖所示

測試結果如下圖所示

---------------------------------------------------------------------------------------------------------------------------------------------------------

來于：http://blog.csdn.net/zitong_ccnu/article/details/11097663

--------------------------------------------------------------------

//關于平衡二叉樹的實現 BBST(Blance binary search tree)
#include <cstdio>
#include <cstdlib>
//#define _OJ_
typedef struct tree
{
??? int data;
??? int height;
??? struct tree *lchild;
??? struct tree *rchild;
} tree, *Bitree;

int
Height(Bitree T)
{
??? if(T == NULL)??? return -1;
??? else? return T->height;
}

int
Max(int h1, int h2)
{
??? return h1 > h2 ? h1 : h2;
}

Bitree
Left(Bitree T)
{
??? Bitree T1;
??? T1 = T->rchild;
??? T->rchild = T1->lchild;
??? T1->lchild = T;

??? T->height? = Max(Height(T->lchild), Height(T->rchild)) + 1;
??? printf("T == %d\n", T->height);

??? T1->height = Max(Height(T1->lchild), Height(T1->rchild)) + 1;
??? printf("T1 == %d\n", T1->height);
??? return T1;
}

Bitree
Right(Bitree T)
{
??? Bitree T1;
??? T1 = T->lchild;
??? T->lchild = T1->rchild;
??? T1->rchild = T;
?
??? T->height? = Max(Height(T->lchild), Height(T->rchild)) + 1;
??? printf("T == %d\n", T->height);
??? T1->height = Max(Height(T1->lchild), Height(T1->rchild)) + 1;
??? printf("T1 == %d\n", T1->height);
??? return T1;
}

Bitree
Left_Right(Bitree T)
//左孩子的右孩子插入元素
{
??? T = Left(T);
??? return Right(T);
}

Bitree
Right_Left(Bitree T)
//右孩子的左孩子插入元素
{
??? T = Right(T);
??? return Left(T);
}


Bitree
Insert(Bitree T, int x)
{
??? if(T == NULL) {
??? T = (Bitree) malloc (sizeof(tree));
??? T->data = x;???????? T->height = 0;
??? T->lchild = T->rchild = NULL;
??? }

??? else if(x < T->data) {
??? T->lchild = Insert(T->lchild, x);
??? if(Height(T->lchild) - Height(T->rchild) == 2) {
??? if(x < T->lchild->data)
??????? T = Right(T);????????????????????? //在左邊左兒子插入元素ll此時右旋
??? if(x > T->lchild->data)
??????? T = Left_Right(T);??????????????? //在左邊右兒子的插入元素lr此時左右旋
??? }
? }

??? else if(x > T->data) {
??? T->rchild = Insert(T->rchild, x);
??? if(Height(T->rchild) - Height(T->lchild) == 2) {
??????? printf("\n%d %d\n", Height(T->rchild), Height(T->lchild));
??????? printf("ok\n");
??? if(x > T->rchild->data)
??????? T = Left(T);?????????????????????? //在右邊右兒子插入元素rr此時左旋
??? if(x < T->lchild->data)
??????? T = Right_Left(T);??????????????? //在右邊左兒子插入元素rl此時右左旋
???? }
? }

??? T->height = Max(Height(T->lchild), Height(T->rchild)) + 1;
??? return T;
}

void
preoder(Bitree T)
{
??? if(T) {
??????? printf("data == %d\n", T->data);
??????? preoder(T->lchild);
??????? printf("\n");
??????? preoder(T->rchild);
??? }
}


int main(int argc, char const *argv[]) {
#ifndef _OJ_ //ONLINE JUDGE
?????? freopen("input.txt", "r", stdin);
?????? //freopen("output.txt", "w", stdout);
#endif
?? ?
??? int a[100];
??? int n;
??? Bitree T = NULL;
??? scanf("%d", &n);
??? for (int i = 0; i < n; i++) {
??????? scanf("%d", &a[i]);??? printf("%d ", a[i]);
??????? T = Insert(T, a[i]);
??? }
??? preoder(T);
??? // printf("%d\n", Height(T));
??? // printf("%d\n", T->data);



?? ?
??? return 0;
}

?