有關莫比烏斯反演

對于兩個定義域為整數的函數F(x)和f(x);

若有:

然后F(x)可以快速求出；

如何用F求解f呢？

莫比烏斯反演：

對于兩個定義域為整數的函數F(x)和f(x);

若有:

則有：

其中μ(x)為莫比烏斯函數，其定義為：

對于（pi為質數）

若對于任意i存在ki＞1,則μ(x)=0；

否則若質因子的個數為偶數，則μ(x)=1；

若質因子的個數為奇數，則μ(x)=-1；

有了這個定義之后；

為什么這是對的呢？

莫比烏斯函數有如下性質：

? ? ? μ(1)=1;

證明：

觀察上式，其含義為x的所有因子的μ和；

若x有重復質因子，則di可能有重復質因子，

但這樣的話μ(di)為零；

把μ為0的部分放在一邊；

剩下各自不含重復質因子的di了；

設x有k種質因子；

則設

顯然，有

于是

多項式定理（楊輝三角）

帶入x=-1,a=1，得證；

于是，莫比烏斯函數有了這樣的性質：

這可以用來證明莫比烏斯反演；

即

?

證明：

?

發現：d的集合完全等于k的集合；

對于每一個k,考慮f(k)對答案的貢獻；

發現在上式中；

當即時

?f(k)對答案貢獻f(k)·μ(d)

于是：

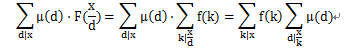
由莫比烏斯函數的性質可知：

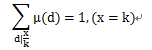
于是

得證；

莫比烏斯反演的另一種形式：

若有

則有

證明思路大同小異，省去；

莫比烏斯函數的求法：

莫比烏斯函數是積性函數（易證）；

于是可線性篩求解；

代碼如下:

void prime(){int i,j;vis[1]=true;mob[1]=1;for(i=2;i<=MAXN;i++){if(!vis[i])pri[++cnt]=i,mob[i]=-1;for(j=1;j<=cnt&&pri[j]*i<=MAXN;j++){vis[i*pri[j]]=true;if(i%pri[j])mob[i*pri[j]]=-mob[i];else{mob[i*pri[j]]=0;break;}}}
}

?