PI校正環節在經典控制論中非常有用,特別是對負反饋控制系統,基本上都有PI校正環節。
1.下面分別說明比例環節和積分環節的作用,以階躍信號為例。
①比例環節單獨作用
以上分析說明,若只有比例環節的控制系統,階躍響應也是一個階躍信號,但會存在一定靜差,且靜差值隨Kp增大而減小,但始終存在,不隨時間變化。
輸出的理論波形跟實際的數字控制輸出波形會不一致。因為實際數字控制系統每隔一個計算周期運算一次,而在這個計算周期中,輸出量只受上一次的調節參數和中間變量的控制。所以可能會出現超調情況。
②比例-積分共同作用
拉氏反變換
以上分析說明,當加入積分項后,階躍響應為一逐漸上升的曲線,且誤差分量隨時間逐漸趨于零;KI越大,誤差分量衰減越快,KP越大,誤差分量衰減越慢。
PI校正環節的優缺點:
比例系數Kp增大,則會減小穩態誤差,減小了上升時間,提高了響應速度,但會引入并逐漸增大超調量,直至系統振蕩;
積分環節提高了系統型別,消除穩態誤差,但參數KI若過大,積分作用太強,會在大偏差階段引起過大超調,調節時間變長,最后振蕩。
2.PI環節的表達式
傳遞函數
微分方程
對應的離散方程為
寫成序列形式
寫出相應的 z 變換系統方程
根據序列形式,可以寫出程序代碼:
#define Ts 0.00001 // 采樣時間
typedef struct PI_Ele{float kp; // 比例環節系數float ki; // 積分環節系數float x1;float x2;float yout;float y1;
} PI_Vector;
#define PI_Macro(PI_Vector v) \ // 算法的宏定義v.yout = (v.kp+v.ki*Ts)*v.x2-v.kp*x1+v.y1; \v.x1 = v.x2; \v.y1 = v.yout; 




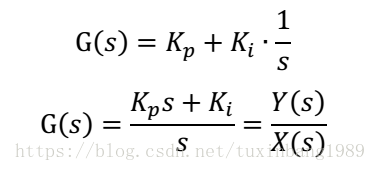
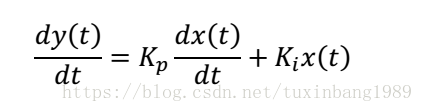
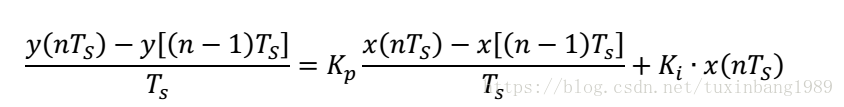
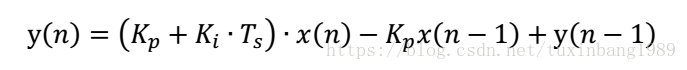
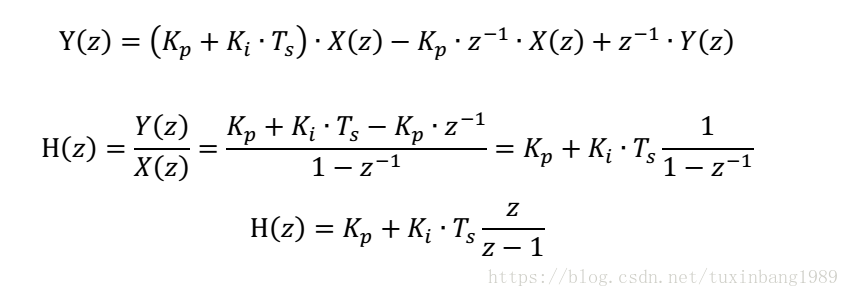
)




)













)