常用的相似度計算

在數據分析和數據挖掘的過程中，我們經常需要知道個體間差異的大小，進而評價個體的相似性和類別。最常見的是數據分析中的相關分析，數據挖掘中的分 類和聚類算法，如K最近鄰（KNN）和K均值（K-Means）。當然衡量個體差異的方法有很多，最近查閱了相關的資料，這里整理羅列下。

　　為了方便下面的解釋和舉例，先設定我們要比較X個體和Y個體間的差異，它們都包含了N個維的特征，即X=（x₁, x₂, x₃, … x_n），Y=（y₁, y₂, y₃, … y_n）。下面來看看主要可以用哪些方法來衡量兩者的差異，主要分為距離度量和相似度度量。

?

距離度量

　　距離度量（Distance）用于衡量個體在空間上存在的距離，距離越遠說明個體間的差異越大。

?

歐幾里得距離(Euclidean Distance)

　　歐氏距離是最常見的距離度量，衡量的是多維空間中各個點之間的絕對距離。公式如下：

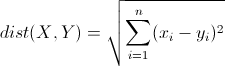
　　因為計算是基于各維度特征的絕對數值，所以歐氏度量需要保證各維度指標在相同的刻度級別，比如對身高（cm）和體重（kg）兩個單位不同的指標使用歐式距離可能使結果失效。

?

明可夫斯基距離(Minkowski Distance)

　　明氏距離是歐氏距離的推廣，是對多個距離度量公式的概括性的表述。公式如下：

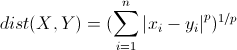
　　這里的p值是一個變量，當p=2的時候就得到了上面的歐氏距離。

?

曼哈頓距離(Manhattan Distance)

　　曼哈頓距離來源于城市區塊距離，是將多個維度上的距離進行求和后的結果，即當上面的明氏距離中p=1時得到的距離度量公式，如下：

?

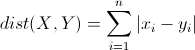
切比雪夫距離(Chebyshev Distance)

　　切比雪夫距離起源于國際象棋中國王的走法，我們知道國際象棋國王每次只能往周圍的8格中走一步，那么如果要從棋盤中A格(x₁, y₁)走到B格(x₂, y₂)最少需要走幾步？擴展到多維空間，其實切比雪夫距離就是當p趨向于無窮大時的明氏距離：

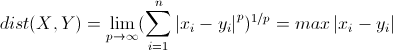
　　其實上面的曼哈頓距離、歐氏距離和切比雪夫距離都是明可夫斯基距離在特殊條件下的應用。

?

馬哈拉諾比斯距離(Mahalanobis Distance)

　　既然歐幾里得距離無法忽略指標度量的差異，所以在使用歐氏距離之前需要對底層指標進行數據的標準化，而基于各指標維度進行標準化后再使用歐氏距離就衍生出來另外一個距離度量——馬哈拉諾比斯距離（Mahalanobis Distance），簡稱馬氏距離。

?

相似度度量

　　相似度度量（Similarity），即計算個體間的相似程度，與距離度量相反，相似度度量的值越小，說明個體間相似度越小，差異越大。

?

向量空間余弦相似度(Cosine Similarity)

　　余弦相似度用向量空間中兩個向量夾角的余弦值作為衡量兩個個體間差異的大小。相比距離度量，余弦相似度更加注重兩個向量在方向上的差異，而非距離或長度上。公式如下：

?

皮爾森相關系數(Pearson Correlation Coefficient)

　　即相關分析中的相關系數r，分別對X和Y基于自身總體標準化后計算空間向量的余弦夾角。公式如下：

?

Jaccard相似系數(Jaccard Coefficient)

　　Jaccard系數主要用于計算符號度量或布爾值度量的個體間的相似度，因為個體的特征屬性都是由符號度量或者布爾值標識，因此無法衡量差異具 體值的大小，只能獲得“是否相同”這個結果，所以Jaccard系數只關心個體間共同具有的特征是否一致這個問題。如果比較X與Y的Jaccard相似系 數，只比較x_n和y_n中相同的個數，公式如下：

?

調整余弦相似度(Adjusted Cosine Similarity)

　　雖然余弦相似度對個體間存在的偏見可以進行一定的修正，但是因為只能分辨個體在維之間的差異，沒法衡量每個維數值的差異，會導致這樣一個情況： 比如用戶對內容評分，5分制，X和Y兩個用戶對兩個內容的評分分別為(1,2)和(4,5)，使用余弦相似度得出的結果是0.98，兩者極為相似，但從評 分上看X似乎不喜歡這2個內容，而Y比較喜歡，余弦相似度對數值的不敏感導致了結果的誤差，需要修正這種不合理性，就出現了調整余弦相似度，即所有維度上 的數值都減去一個均值，比如X和Y的評分均值都是3，那么調整后為(-2,-1)和(1,2)，再用余弦相似度計算，得到-0.8，相似度為負值并且差異 不小，但顯然更加符合現實。

?

歐氏距離與余弦相似度

　　歐氏距離是最常見的距離度量，而余弦相似度則是最常見的相似度度量，很多的距離度量和相似度度量都是基于這兩者的變形和衍生，所以下面重點比較下兩者在衡量個體差異時實現方式和應用環境上的區別。

　　借助三維坐標系來看下歐氏距離和余弦相似度的區別：

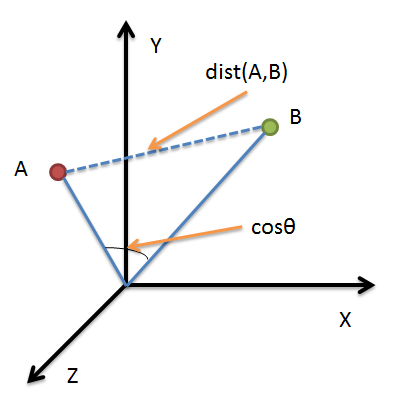
　　從圖上可以看出距離度量衡量的是空間各點間的絕對距離，跟各個點所在的位置坐標（即個體特征維度的數值）直接相關；而余弦相似度衡量的是空間向 量的夾角，更加的是體現在方向上的差異，而不是位置。如果保持A點的位置不變，B點朝原方向遠離坐標軸原點，那么這個時候余弦相似度cosθ是保持不變 的，因為夾角不變，而A、B兩點的距離顯然在發生改變，這就是歐氏距離和余弦相似度的不同之處。

?

　　根據歐氏距離和余弦相似度各自的計算方式和衡量特征，分別適用于不同的數據分析模型：歐氏距離能夠體現個體數值特征的絕對差異，所以更多的用于 需要從維度的數值大小中體現差異的分析，如使用用戶行為指標分析用戶價值的相似度或差異；而余弦相似度更多的是從方向上區分差異，而對絕對的數值不敏感， 更多的用于使用用戶對內容評分來區分用戶興趣的相似度和差異，同時修正了用戶間可能存在的度量標準不統一的問題（因為余弦相似度對絕對數值不敏感）。

?

　　上面都是對距離度量和相似度度量的一些整理和匯總，在現實的使用中選擇合適的距離度量或相似度度量可以完成很多的數據分析和數據挖掘的建模，后續會有相關的介紹。

附件為python部分相似度算法：

#!/usr/bin/python
#coding=utf-8
critics = {
?

'Lisa':{
??????? 'Lady in the water':2.5,
??????? 'Snake on a plane' :3.5
??? },
??? 'Tom':{
??????? 'Lady in the water':3.0,
??????? 'Snake on a plane' :4.0
??? },
??? 'Jerry':{
??????? 'Lady in the water':2.0,
??????? 'Snake on a plane' :3.0
??? },
??? 'WXM':{
??????? 'Lady in the water':3.3,
??????? 'Snake on a plane' :4.2
??? },
??? 'jhz':{
??????? 'Lady in the water':3.9,
??????? 'Snake on a plane' :4.5
??? }
}

from math import sqrt
"""
歐幾里得空間法 計算相似度
"""
def sim_distance(p1, p2):
??? c = set(p1.keys())&set(p2.keys())
??? if not c:
??????? return 0
??? sum_of_squares = sum([pow(p1.get(sk)-p2.get(sk),2) for sk in c])
??? p = 1/(1+sqrt(sum_of_squares))
??? return p
?
"""
皮爾遜相關度
"""
def sim_distance_pearson(p1,p2):
??? c = set(p1.keys())&set(p2.keys())
??? if not c:
??????? return 0
??? s1 = sum([p1.get(sk) for sk in c])
??? s2 = sum([p2.get(sk) for sk in c])
??? sq1 = sum([pow(p1.get(sk),2) for sk in c])
??? sq2 = sum([pow(p2.get(sk),2) for sk in c])
??? ss = sum([p1.get(sk)*p2.get(sk) for sk in c])
??? n = len(c)
??? num = ss-s1*s2/n
??? den = sqrt((sq1-pow(s1,2)/n)*(sq2-pow(s2-2)/n))
??? if den == 0:
??????? return 0
??? p = num/den
??? return p
?
"""
Jaccard系數
"""
def sim_distance_jaccard(p1,p2):
??? c = set(p1.keys())&set(p2.keys())
??? if not c:
??????? return 0
??? ss = sum([p1.get(sk)*p2.get(sk) for sk in c])
??? sq1 = sum([pow(sk,2) for sk in p1.values()])
??? sq2 = sum([pow(sk,2) for sk in p2.values()])
??? p = float(ss)/(sq1+sq2-ss)
??? return p
?
"""
余弦相似度
"""
def sim_distance_cos(p1,p2):
??? c = set(p1.keys())&set(p2.keys())
??? if not c:
??????? return 0
??? ss = sum([p1.get(sk)*p2.get(sk) for sk in c])
??? sq1 = sqrt(sum([pow(p1.get(sk),2) for sk in p1.values()]))
??? sq2 = sqrt(sum([pow(p2.get(sk),2) for sk in p2.values()]))
??? p = float(ss)/(sq1*sq2)
??? return p

"""
得到top相似度高的前幾位
"""
def topMatches(prefs,person,n=5,similarity=sim_distance_pearson):
??? scores = [similarity(prefs,person,other) for other in prefs if other != person]
??? scores.sort()
??? scores.reverse()
??? return scores[0:n]

"""
#利用所有他人評價值加權平均,為某人提供建議.
"""
def getRecommendations(prefs, person, similarity=sim_distance):
??? totals = {}
??? simSums = {}
?
??? for other in prefs:
??????? if other == person: continue
??????? sim = similarity(prefs,person,other)
??????? #忽略評價值為0或小于0的情況.
??????? if sim<=0: continue
??????? for item in prefs[other]:
??????????? #只對自己還未曾看過的影片進行評價.
??????????? if item not in prefs[person] or prefs[person][item] == 0 :
?????????????? totals.setdefault(item, 0)
?????????????? totals[item] += sim*prefs[other][item]
?????????????? #相似度之和
?????????????? simSums.setdefault(item, 0)
?????????????? simSums[item] += sim
??????? #建立一個歸一化的列表.
??????? rankings = [(total/simSums[item],item) \
??????????????????? for item,total in totals.items()]
??????? rankings.sort()
??????? rankings.reverse()
??????? return rankings

參考文獻:

[1]http://webdataanalysis.net/reference-and-source/distance-and-similarity/
[2]http://wpxiaomo.sinaapp.com/archives/424
[3]http://wpxiaomo.sinaapp.com/archives/423
[4]集體智慧編程