前言:這是蒟蒻第一次寫算法系列,請諸位大佬原諒文筆與排版。
?
?
一、導入
在刷題的時候,我們有時會見到這樣一類問題:在區間$[l,r]$內,共有多少個整數滿足某種條件。如果$l$和$r$間的差很小,我們可以考慮暴力枚舉直接判斷。然而,若$l<=r<=10^9$甚至更大呢?
這時往往就可以用到一種dp方式:數位dp。
?
二、做法:
這里先放一道例題:1026: [SCOI2009]windy數。
題意:求在區間$[l,r]$內,滿足相鄰數位的差>=2的整數的個數。
首先我們可以發現,$[l,r]$的答案=$[1,r]$的答案-$[1,l)$的答案。于是我們可以把問題轉化為求$[1,r]$和$[1,l-1]$的答案。因為$l<=r<=2*10^9$,所以暴力枚舉肯定行不通。但是我們可以發現這道題中整數需滿足的條件只與相鄰數位有關,這啟示我們,也許可以按位dp?
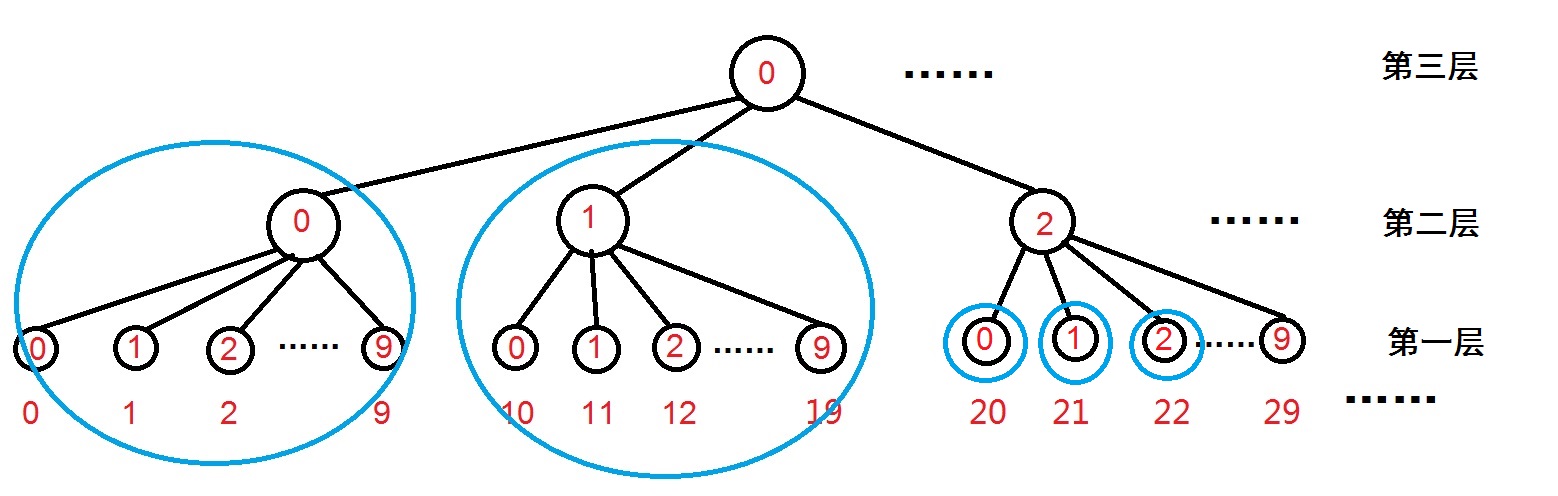
我們先來看一張經典的圖(表示區間$[0,22]$):
?
這幅圖中把正整數按位用樹的形式表示,那么區間$[0,x]$(這里x=22)就可以拆成多棵滿10叉樹(即圖中的藍圈),而且因為每層所用的樹個數不會超過10棵(0~9),總共有$\log_{10}{x}$層,則樹的個數規模為$O(10\log{x})$。
那么單棵滿10叉樹的答案怎么求呢?我們仔細觀察這棵樹,那么就可以發現每棵滿10叉樹表示的數是位數相同(等于它從下往上數所處的層數),最高位相同(等于根節點表示的數),且該樹的答案只與以樹根的10個兒子為根的,10棵子樹的答案有關。并且在整棵樹中,處在同一層的,且子樹根節點表示的數相同的樹(即位數相同,最高位相同),它們是等價的。于是我們就可以直接設$f[i][j]$表示有i位,最高位為j的滿足條件的整數的個數,然后xjb轉移。于是就可以優哉游哉地dp, 然后按圖統計答案了。
不過這道題還是比較麻煩,因為需要排除前導零的影響,不過核心思想還是上面的那樣,然后再分位數統計就好了。
代碼(時間復雜度$O(10^2\log{r})$):


#include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<ctime> #include<algorithm> #include<queue> #include<vector> #include<map> #define ll long long #define ull unsigned long long #define max(a,b) (a>b?a:b) #define min(a,b) (a<b?a:b) #define lowbit(x) (x& -x) #define mod 1000000007 #define inf 0x3f3f3f3f #define eps 1e-18 #define maxn 100020 inline ll read(){ll tmp=0; char c=getchar(),f=1; for(;c<'0'||'9'<c;c=getchar())if(c=='-')f=-1; for(;'0'<=c&&c<='9';c=getchar())tmp=(tmp<<3)+(tmp<<1)+c-'0'; return tmp*f;} inline ll power(ll a,ll b){ll ans=0; for(;b;b>>=1){if(b&1)ans=ans*a%mod; a=a*a%mod;} return ans;} inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} inline void swap(int &a,int &b){int tmp=a; a=b; b=tmp;} using namespace std; int f[20][10]; int l,r; int dp(int x) {int num[20],len=0;for(;x;x/=10)num[++len]=x%10;for(int i=0;i<=9;i++)f[1][i]=1;//預處理 for(int i=2;i<=len;i++)for(int j=0;j<=9;j++){f[i][j]=0;for(int k=0;k<=9;k++)if(abs(j-k)>=2)f[i][j]+=f[i-1][k];}//處理f數組,f[i][j]表示有i位,最高位為j的的windy數個數*/ int ans=0;for(int i=1;i<len;i++)for(int j=1;j<=9;j++)ans+=f[i][j];//統計位數小于len的數一定小于n,直接加上 for(int i=len;i;i--){int l=(i==len)?1:0,r=(i==1)?num[i]:num[i]-1;//不含前導零,所以最高位不能取0,從1開始枚舉,否則從0開始//除個位以外,因當前位若取num[i]可能超出1~n的范圍,所以只能取到num[i]-1;因為詢問1~n時包含n,所以個位的上限要取num[i]for(int j=l;j<=r;j++)if(i==len||abs(j-num[i+1])>=2)ans+=f[i][j];if(i<len&&abs(num[i]-num[i+1])<2)break;//統計下一位時,這一位取的是num[i],若會和上一位num[i+1]發生沖突,則不可能出現windy數,直接break掉 }return ans; } int main() {l=read(); r=read();printf("%d\n",dp(r)-dp(l-1)); }
?
?
三、歸納:
數位dp的特征:數據規模大,統計整數個數,被統計的數滿足的條件往往與數位之間的關系或數位間的運算有關。
基本做法:差分,先按位dp出所需數據($f[i][S]$->i位數,狀態為S),然后再拆分原區間,用dp出的數據統計。
?
?
四、其他例題:
1、【bzoj1833】[ZJOI2010] count 數字計數
裸的數位dp,分別計算每個數字出現的次數,做法和上面類似。
代碼:


#include<cstdio> #include<cmath> #include<cstdlib> #include<cstring> #include<ctime> #include<iostream> #include<algorithm> #include<queue> #include<vector> #include<map> #define ll long long #define ull unsigned long long #define max(a,b) (a>b?a:b) #define min(a,b) (a<b?a:b) #define lowbit(x) (x& -x) #define mod 1000000007 #define inf 0x3f3f3f3f #define eps 1e-18 #define maxn 100010 inline ll read(){ll tmp=0; char c=getchar(),f=1; for(;c<'0'||'9'<c;c=getchar())if(c=='-')f=-1; for(;'0'<=c&&c<='9';c=getchar())tmp=(tmp<<3)+(tmp<<1)+c-'0'; return tmp*f;} inline ll power(ll a,ll b){ll ans=1; for(;b;b>>=1){if(b&1)ans=ans*a%mod; a=a*a%mod;} return ans;} inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} inline void swap(int &a,int &b){int tmp=a; a=b; b=tmp;} using namespace std; ll f[20][10][10],base[20]; ll l,r; void prework() {base[0]=1;for(int i=1;i<=13;i++)base[i]=base[i-1]*10;for(int i=0;i<=9;i++)f[1][i][i]=1;for(int i=2;i<=13;i++)for(int j=0;j<=9;j++){ll x=f[i-1][0][0]+f[i-1][0][1]*9;for(int k=0;k<=9;k++){f[i][j][k]=(j==k?base[i-1]:0)+x;}} } ll solve(ll n,int num) {if(n<0)return 0;ll tmp=++n;//這里++n是為了把閉區間轉化為開區間,因為下面求解時1~n的答案并不包括n。。int a[20],len=0;for(;tmp;tmp/=10)a[++len]=tmp%10;for(int i=1;i<len;i++)for(int j=1;j<=9;j++)ans+=f[i][j][num];for(int i=len;i;i--){for(int j=(i==len?1:0);j<a[i];j++)ans+=f[i][j][num];n-=a[i]*base[i-1];if(a[i]==num)ans+=n;}return ans; } int main() {prework();l=read(); r=read();for(int i=0;i<9;i++)printf("%lld ",solve(r,i)-solve(l-1,i));printf("%lld\n",solve(r,9)-solve(l-1,9)); }
?



)





)
——轉載圖片...)






的使用示例)

