最短路徑——Dijkstra算法以及二叉堆優化（含證明）

一般最短路徑算法習慣性的分為兩種：單源最短路徑算法和全頂點之間最短路徑。前者是計算出從一個點出發，到達所有其余可到達頂點的距離。后者是計算出圖中所有點之間的路徑距離。

---

單源最短路徑

Dijkstra算法

思維

本質上是貪心的思想，聲明一個數組dis來保存源點到各個頂點的最短距離和一個保存已經找到了最短路徑的頂點的集合：S，原本的元素構成集合Q，初始時，原點 s 的路徑權重被賦為 0 （dis[s] = 0）。若對于頂點 s 存在能直接到達的邊（s,m），則把dis[m]設為w（s, m）,同時把所有其他（s不能直接到達的）頂點的路徑長度設為無窮大。初始時，集合S只有頂點s

然后，從dis數組選擇最小值，則該值就是源點s到該值對應的頂點的最短路徑，并且把該點加入到S中，此時完成一個頂點， 然后，我們需要看看新加入的頂點是否可以到達其他頂點并且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短，如果是，那么就替換這些頂點在dis中的值。 然后，又從dis中找出最小值，重復上述動作，直到S中包含了圖的所有頂點。
但是很可惜，由于算法特性，一個點的距離確定后不會再改變，這里的確定不是指得到數值，而且該點被作為觀察點觀察后所以這個算法并不能處理帶負權邊的圖。

但是可以利用該算法+優先隊列來優化，優化后的算法打破了之前的一個點的距離確定后不會再改變的算法特性，更加類似SPFA，并且可以處理負權邊。但個人覺得已經不能稱作dijkstra算法了。

---

證明

這里給出一個命題：從集合Q中找到dis[k]最小的v，dis[k]即為源點到v的最短路徑長度。
如果這個命題為真，dij的正確性就可以得證。

• 證明：從開始利用算法取得一個v₁，即dis[v₁]是最小的，\(\forall\)v，dis[v]>dis[v₁]。
  假設dis[v₁]不是從源點到v₁最短路徑
  則\(\exists\)v，使得dis[v]<dis[v₁]，與已知矛盾。
  得證。
• 證明：已利用算法從Q中找到k個點，并確定了k個點的最短路徑，此時再從Q中用算法找出一個v_k+1，dis[v_k+1]即為源點到v_k+1最短路徑。
  假設dis[v_k+1不是源點到v_k+1的最短路徑長度。
  則設從源點到v_k+1的最短路徑經過的點的集合為V，dis為路徑長度，切dis < dis[v_k+1]。
  設V中最靠近v_k+1且不屬于S的點為v_x，v_x的后繼點為v_y
  。如果有向圖中皆為正權邊，則易得dis[v_x] < dis[v_y] <= dis。（v_y = v_k+1時等號成立）
  但又因為v_x不屬于S，則dis[v_x] > dis，矛盾。
  得證。
• 綜上所述，命題得證。
• 負權邊的時候，dis[v_x] < dis[v_y]和dis[v_x] > dis都不一定成立。故不得證。

---

舉例演算

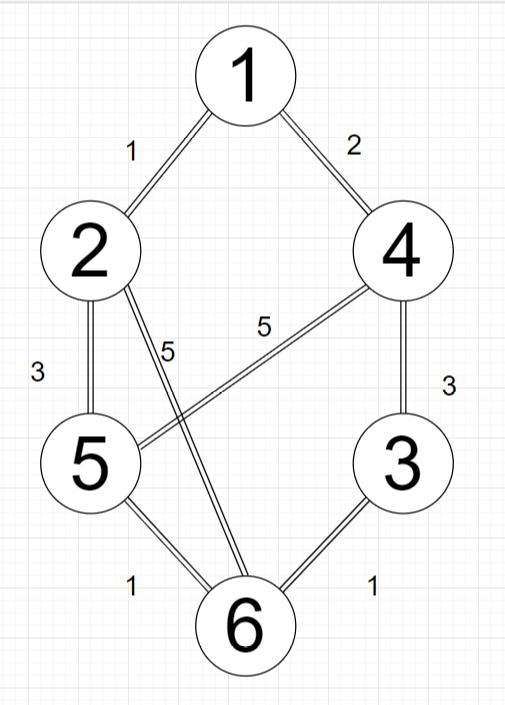
集合S	當前觀察點u	dis[2]	dis[3]	dis[4]	dis[5]	dis[6]
1	-	1	∞	2	∞	∞
1,2	2	1	∞	2	4	6
1,2,4	4	1	5	2	4	6
1,2,4,5	5	1	5	2	4	6
1,2,4,5,3	3	1	5	2	4	5
1,2,4,5,3,6	6	1	5	2	4	5

從結點1出發，1與2、4連通，確定（1，2），（1，4）的距離，其中到2的距離最短，再從觀察點2出發，2與5、6連通，根據dis[u]+c[u][v]<dis[v]的判斷關系出發，更新dis。接著再分別從觀察點4，5，3，6出發更新dis，得到最終的結點1的單源最短路徑。

---

代碼實現

樸素dij算法，時間復雜度約為O(n²)

#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>using namespace std;const int maxn = 1000;
const int inf = 0x7fffffff;int n, m;
int e[maxn][maxn], dis[maxn];
int book[maxn];void dij(int s) {for (int i = 1; i <= n; i++) dis[i] = e[s][i];for (int i = 1; i <= n; i++) book[i] = 0;book[s] = 1;dis[s] = 0;for (int i = 1; i <= n - 1; i++) {int min = inf;int u;for (int j = 1; j <= n; j++) {if (book[j] == 0 && dis[j] < min) {min = dis[j];u = j;}}book[u] = 1;for (int v = 1; v <= n; v++) {if (e[u][v] < inf && book[v] == 0) {if (dis[v] > dis[u] + e[u][v]) {dis[v] = dis[u] + e[u][v];}}}}
}int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {e[i][j] = inf;}}for (int i = 0; i < m; i++) {int u, v, w;cin >> u >> v >> w;e[u][v] = w;}int x;cin >> x;dij(x);for (int i = 1; i <= n; i++) {cout << dis[i] << " ";}return 0;
}

為了能夠方便的尋找當前最小的dis作為觀察點，可以利用優先隊列最小堆來優化。同時利用初始化建表來節省尋找每個點的相鄰點的過程。這里使用的是stl中的優先隊列，底層是heap實現的，應該是二叉堆，所以時間復雜度應該是O((m+n)logn)，如果是使用斐波那契堆，可以到O(nlogn)。

#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>using namespace std;const int MAX = 1000;int h[MAX * 2], to[MAX * 2], nxt[MAX * 2], co[MAX * 2], dis[MAX], k = 0, n, m;
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > que;void insert(int u,int v,int c) {nxt[++k] = h[u];h[u] = k;to[k] = v;co[k] = c;nxt[++k] = h[v];h[v] = k;to[k] = u;co[k] = c;
}void dij(int s) {for (int i = 0; i < MAX; i++) dis[i] = 0x7FFFFFFF;dis[s] = 0;que.push(make_pair(dis[s], s));while (!que.empty()) {pair<int, int> u = que.top();que.pop();if (dis[u.second] < u.first) continue;for (int i = h[u.second]; i; i = nxt[i]) {if (dis[to[i]] > dis[u.second] + co[i]) {dis[to[i]] = dis[u.second] + co[i];que.push(make_pair(dis[to[i]], to[i]));}}}
}int main() {cin >> n >> m;memset(h, 0, sizeof(h));int u, v, c;for (int i = 0; i < m; i++) {cin >> u >> v >> c;insert(u, v, c);}int x;cin >> x;dij(x);for (int i = 1; i <= n; i++) {if (dis[i] > 100000) cout << "none" << " ";else cout << dis[i] << " ";}cout << endl;return 0;
}