分類：機器人學

一、問題描述

? 如右圖所示的三自由度機械臂，關節1和關節2相互垂直，關節2和關節3相互平行。如圖所示，所有關節均處于初始狀態。 ? 要求: (1) 定義并標注出各關節的正方向； (2) 定義機器人基坐標系｛0｝及連桿坐標系｛1｝，｛2｝，｛3｝； (3) 求變換矩陣 , , ； (4) 根據末端腕部位置 (x, y, z) 返求出對應關節 ， ， ； (5) 利用軟件繪制出機器人模型的三維點線圖，并控制機器人腕部沿半徑r=0.1的圓弧運動. ?

?

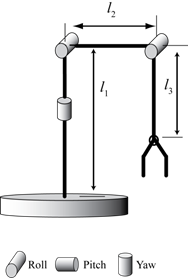
二、任務求解

2.1建立坐標系

?

?

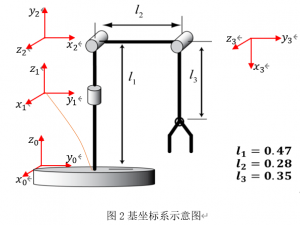
2.2?變換矩陣

2.2.1?變換求解

??（1）連桿坐標系｛1｝——基坐標系｛0｝?? 原點重合，可繞z軸任意旋轉 ?

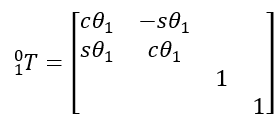
??（2）連桿坐標系｛2｝——連桿坐標系｛1｝?先繞x軸旋轉90°，再繞新得到的y軸旋轉90°，然后沿新得到的y軸平移 ，最后得到的坐標系可繞z軸任意旋轉 ???3）連桿坐標系｛3｝——連桿坐標系｛2｝?? 繞z軸旋轉-90°，再沿新得到的y軸平移 ，最后得到的坐標系可繞z軸任意旋轉 ??

2.2.2?物理意義求解

? 變換矩陣的前三列，每列值對應的數為變換坐標系的坐標軸x、y、z在基坐標系中的坐標位置，第四列為變換坐標系的原點在基坐標系中的坐標位置，第四行為齊次補行數據，則可根據坐標系的位置直接列出下式： ?

? 可見，兩種方式的結果表達式一致。

2.2.3?變換矩陣終解

?

?

2.3?逆運動學求解

2.3.1?矩陣逆推導

? 由連桿坐標系｛3｝到基座坐標系｛0｝的齊次矩陣可以表示為 ?

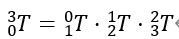
? 末端執行器的位置在基座坐標系｛0｝中的描述為 ?? 末端執行器的位置在基座坐標系｛0｝中的描述為 ?? 關系為： ?? 根據矩陣對應元素相等，由MATLAB計算可得可得下面等式： ?

x=-(7*cos(a2)*sin(a1))/25-(7*cos(a2)*sin(a1)*sin(a3))/20(7*cos(a3)*
sin(a1)*sin(a2))/20
y=(7*cos(a1)*cos(a2))/25+(7*cos(a1)*cos(a2)*sin(a3))/20+(7*cos(a1)*cos(a3)*sin(a2))/20
z=(7*sin(a2))/25 + (7*sin(a2)*sin(a3))/20 - (7*cos(a2)*cos(a3))/20 + 47/100

由 ?

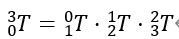
? 則： ?? 由對應元素相等，得：

(x*cos(a1))/(cos(a1)^2 + sin(a1)^2) + (y*sin(a1))/(cos(a1)^2 + sin(a1)^2)=0(y*cos(a1))/(cos(a1)^2 + sin(a1)^2) - (x*sin(a1))/(cos(a1)^2 + sin(a1)^2)=(7*cos(a2))/25+(7*cos(a2)*sin(a3))/20+(7*cos(a3)*sin(a2))/20z=(7*sin(a2))/25 + (7*sin(a2)*sin(a3))/20 - (7*cos(a2)*cos(a3))/20 + 47/100

? 綜上可得， ?

?

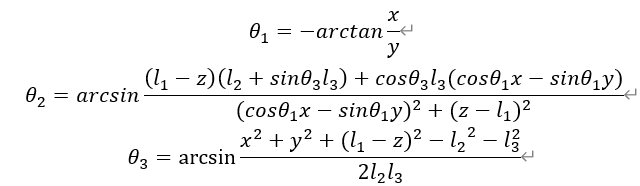
2.3.2?幾何推導

? 在x0y平面，將末端執行器的軌跡投影到該平面，藍色表示原位置，橘色代表移動后的位置，黑色坐標系為基坐標系，如下圖： ?

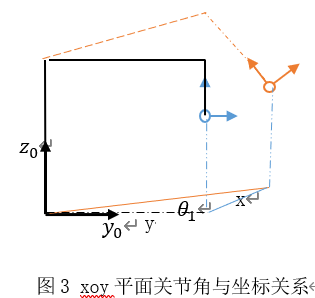
? 由圖易見， 為末端執行器投影到xoy平面x與y的夾角，（逆時針為正）, ?? 在y0z平面，將末端執行器的軌跡投影到該平面，藍色表示原位置，橘色代表移動后的位置，黑色坐標系為基坐標系，如下圖： ? ??? 將末端執行器的軌跡投影到下圖所示平面，藍色表示原位置，橘色代表移動后的位置，黑色坐標系為基坐標系，如下圖： ?? 構建直角三角形，可得： ?? 綜上，得各關節角與坐標位置的關系為： ??

三、D-H模型法求解

3.1?坐標系建立

? 0號桿件固連在基座上，建立基坐標系 ?

?

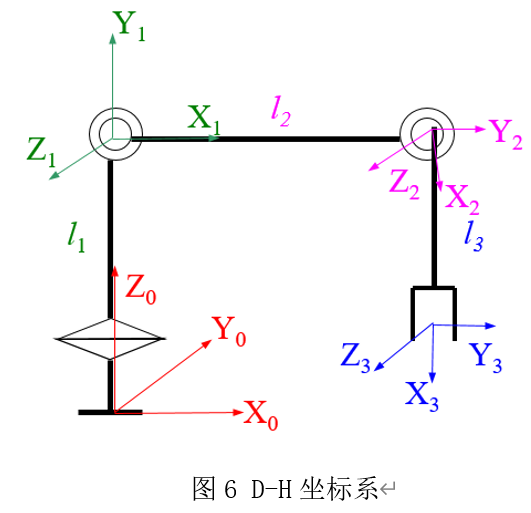
3.2 D-H參數

?

?

3.3?各關節變換矩陣

? 若已知四個參數就完全確定了兩連桿之間的相對關系。對此，我們建立基坐標系和連桿運動坐標系之間的變換關系。對于旋轉關節可以確定以下的齊次矩陣 ? 即先繞x軸旋轉， ?

? 然后沿x軸移動，再沿基坐標系的z軸移動d，最后繞z軸旋轉 ? 將參數代入上式，由此可以得到各關節變換矩陣 ??

3.4?求逆變換

? 同2.3.1 ?

四、軟件仿真

4.1?程序代碼

? 用軟件python(x,y)編寫代碼，如下： ?

?

4.2?仿真結果

?

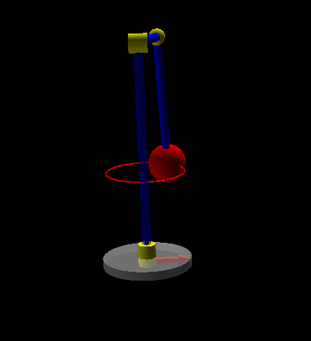
運動學建模仿真Python