[學習筆記]支配樹

被支配樹支配的恐懼

定義

顯然，這個支配關系是一個樹（或者如果有的點不能從r到達，就是一個樹+一堆點）。

首先不會成環，其次也不會是DAG

即如果A支配C，B支配C，那么A和B之間必然有支配關系

解法

首先是DAG很好做：

[ZJOI2012]災難

一般有向圖：有環的存在，不能topo

方法分三步：

轉化為找半支配點

idom[x]表示x的支配點編號

sdom[x]表示x的半支配點編號

先找到原圖一個生成樹，找到每個點的dfn序

?

定義半支配關系為：

定義半支配點為：

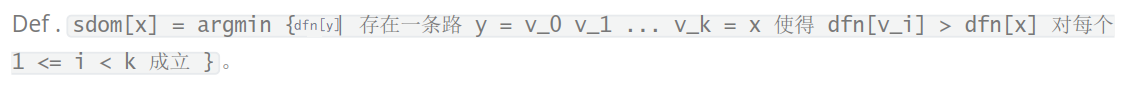
即滿足支配關系dfn最小的點

?

一些認識：

A對于dfs樹

B對于支配和半支配

?

半支配點也一定是x在dfs樹上的祖先

?

請大量運用反證法和dfs算法的深度優先性質進行證明

?

雖然sdom[x]可能不是idom[x]

但是可以斷言：

證明：

實在不懂可以畫圖感性理解

?

所以如果知道sdom[x],現在已經可以專化為求DAG的支配樹了

?

如何找半支配點

?這個做法就是前面兩個認識的兩種情況。

dfn[z]>dfn[y]啟發我們倒序處理

這樣，x在T'的祖先z一定都是之前加入的，一定比y的dfn大，直接取即可。

實現維護T'？

改進：同時找支配點

?

（fix：每個點從一個祖先連過來恰好一條邊）

證明略

直接看算法流程吧：

從簡化之后的G'角度進行考慮（基本上就是一個樹形結構了），就很好理解了。

補充：

第5步之所以找fa[y]，因為先有第4步，使得當前的根是fa[y]，（4/5兩步交換，就可以直接處理sdom[x]=y的點x了）

第6步的標記還原：必須dfs序正序處理。打標記，如果沒有idom[x]=sdom[x]，那么進行處理。

開始時候，令sdom[x]=x可以省去很多麻煩！！

Code

注意比較函數的書寫。argmin與argmax

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}namespace Miracle{
const int N=2e5+5;
const int M=3e5+5;
int n,m;
struct node{int nxt,to;
}e[M];
int hd[N],cnt;
void add(int x,int y){e[++cnt].nxt=hd[x];e[cnt].to=y;hd[x]=cnt;
}
vector<int>mem[N],fr[N];
int fa[N],dfn[N],fdfn[N],idom[N],sdom[N],df;
int gf[N],val[N];
bool cmp(int x,int y){//x<y?return dfn[sdom[x]]<dfn[sdom[y]];
}
int chm(int x,int y){return dfn[x]<dfn[y]?x:y;
}
int fin(int x){if(gf[x]==x) return x;int rt=fin(gf[x]);val[x]=cmp(val[x],val[gf[x]])?val[x]:val[gf[x]];return gf[x]=rt;
}
void dfs(int x){dfn[x]=++df;fdfn[df]=x;for(reg i=hd[x];i;i=e[i].nxt){int y=e[i].to;if(dfn[y]) continue;fa[y]=x;dfs(y);}
}
void wrk(){for(reg i=n;i>=2;--i){int x=fdfn[i];for(reg j=0;j<(int)fr[x].size();++j){int y=fr[x][j];if(dfn[y]<dfn[x]){sdom[x]=chm(y,sdom[x]);}else{int haha=fin(y);sdom[x]=chm(sdom[val[y]],sdom[x]);}}mem[sdom[x]].push_back(x);gf[x]=fa[x];x=fa[x];for(reg j=0;j<(int)mem[x].size();++j){int y=mem[x][j];int haha=fin(y);if(sdom[val[y]]==sdom[y]) idom[y]=sdom[y];else idom[y]=val[y];}}for(reg i=2;i<=n;++i){int x=fdfn[i];if(idom[x]!=sdom[x]) idom[x]=idom[idom[x]];}
}
int sz[N];
void sol(int x){sz[x]=1;for(reg i=hd[x];i;i=e[i].nxt){int y=e[i].to;sol(y);sz[x]+=sz[y];}
}
int main(){rd(n);rd(m);int x,y;for(reg i=1;i<=m;++i){rd(x);rd(y);add(x,y);fr[y].push_back(x);}dfs(1);    for(reg i=1;i<=n;++i){sdom[i]=i,val[i]=i,gf[i]=i;}wrk();memset(hd,0,sizeof hd);cnt=0;for(reg i=2;i<=n;++i){add(idom[i],i);}// prt(dfn,1,n);// prt(fa,1,n);// prt(sdom,1,n);// prt(idom,1,n);sol(1);prt(sz,1,n);return 0;
}}
signed main(){Miracle::main();return 0;
}/*Author: *Miracle*
*/

例題

其實就是[ZJOI2012]災難

別的沒什么題目。。。。