圖的基本知識

1.簡介

圖（Graph）是由頂點的有窮非空集合和頂點之間的邊的集合組成，通常表示為：G(V,E)，G表示一個圖，V是圖G中頂點的集合，E是圖G中邊的集合。

圖是一種復雜的非線性結構，在圖結構中，每個元素都可以有零個多個前驅，也可以有零個或多個后繼，元素之間的關系是任意的。

2.分類

圖分無向圖和有向圖

無向圖：由頂點和邊構成；

有向圖：由頂點和弧（有向邊）構成，弧分弧頭和弧尾

多重圖：關聯一對頂點的無向邊（或有向邊，邊的方向一致）多于1條（稱這些邊為平行邊）

簡單圖：既不含平行邊也不含環的圖成為簡單圖

（有向）完全圖：如果任意兩個頂點之間都存在邊叫完全圖，有向的邊叫有向完全圖

連通圖：在無向圖G中，任意兩個頂點是相通的就是連通圖

網：圖中的邊帶權值的話，叫網

3.圖的頂點和邊

頂點的度：頂點關聯邊的數目

有向圖中：入度，方向指向頂點的邊；出度，方向背向頂點的邊

路徑長度：路徑上邊或弧的數目

4.存儲結構

4.1.鄰接矩陣

圖的鄰接矩陣存儲方式是用兩個數組來表示圖。一個一維數組存儲圖中頂點信息，一個二維數組（稱為鄰接矩陣）存儲圖中的邊或弧的信息。

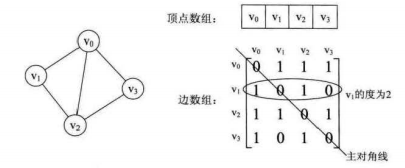
實際中，我們發現對于邊數相對頂點較少的圖，這種結構存在對存儲空間的極大浪費。

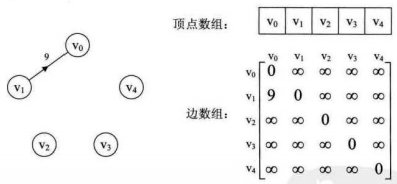
4.2.鄰接表

圖的鄰接表存儲方式是用一個一維數組存頂點，數組中每一項還需要存儲指向下一個鄰接點的指針，以便于查找該頂點的邊信息。圖中每個頂點的所有鄰接點構成一個線性表，由于鄰接點不定，故用單鏈表存儲。

?

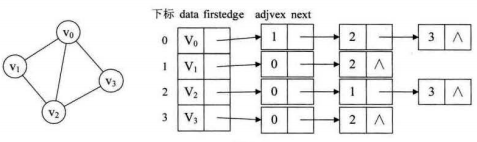
5.遍歷

5.1.深度優先遍歷

深度優先遍歷（DFS，也稱深度優先搜索）：假設給定圖G的初態是所有頂點均未曾訪問過。在圖G中任選一點Vi為初始出發點（源點），則深度優先遍歷如下：首先訪問出發點Vi，并將其標記為已訪問過；然后依次從Vi出發探索Vi的每個鄰接點Wj。若Wj未曾訪問過，則以Wj為新的出發點繼續進行深度優先遍歷，直至圖中所有與源點Vi有路徑相通的頂點均已被訪問為止。如此時圖中任有未被訪問的頂點，則另選一個尚未訪問的頂點作為新的源點重復上述過程，直至圖中所有頂點均已被訪問為止。

5.2.廣度優先遍歷

廣度優先遍歷（BFS，也稱廣度優先搜索）：這是一種盲目搜索法，它會系統的展開并檢查圖中的所有節點，不考慮搜索目標，一層一層逐層向下遍歷，直至遍歷完整張圖。

?

參考資料：《大話數據結構》