模意義下的FFT算法

//寫在前面 單就FFT算法來說的話，下面只給出個人認為比較重要的推導，詳細的介紹可參考　　FFT算法學習筆記

令v[n]是長度為2N的實序列，V[k]表示該實序列的2N點DFT。定義兩個長度為N的實序列g[n]和h[n]為

?g[n]=v[2n],　　h[n]=v[2n+1],　　0<=n<N?

則可進行如下推導

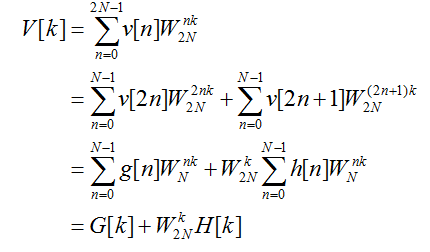
這里所用的FFT算法能夠實現O(nlogn)復雜度的離散傅里葉變換和上面最后所得的關系密切相關。

?

下面進入正題——模意義下的FFT

還是需要先了解一下關于 復序列的DFT的對稱性質及一些補充定義?

由此，可以試想，假設說要模的素數p為1e8級別大小，那么我們可以把原始的實序列x[n]“拆”一下。

下面假設我們要求的是x[n]卷積y[n]的結果t[n]。

假設q是sqrt(p)級別的一個數，我們可以把x[n]/q存到復序列x1[n]的實部，x[n]%q存到復序列x1[n]的虛部。這時，對x1[n]、y1[n]求DFT，再由X1[k]*Y1[k]得到T1[k],整個運算過程中能夠產生的最大浮點數為N*q^2級別，一般來說還是在可以接受的范圍內的。

接下來考慮從卷積結果{T1[k]}中恢復出原始的t[n]的過程。

看一下T1[k]的組成

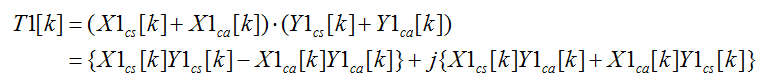
到這里差不多就可以結束了。發現上面最后一行等號右邊有四個“乘積”，我們可以把上面四個乘積分別單獨拿出來，求IDFT就可以恢復出x/y_re/im卷積的結果，之后針對不同的乘積，考慮需要在模p意義下乘上q^2、q^1或q^0，來進行恢復就可以了。

奉上模板

namespace FFT_MO    //前面需要有 mod(1e8~1e9級別),upmo(a,b) 的定義 
{const int FFT_MAXN=1<<18;const db pi=3.14159265358979323846264338327950288L;struct cp{db a,b;cp(double a_=0,double b_=0){a=a_,b=b_;}cp operator +(const cp&rhs)const{return cp(a+rhs.a,b+rhs.b);}cp operator -(const cp&rhs)const{return cp(a-rhs.a,b-rhs.b);}cp operator *(const cp&rhs)const{return cp(a*rhs.a-b*rhs.b,a*rhs.b+b*rhs.a);}cp operator !()const{return cp(a,-b);}}nw[FFT_MAXN+1],f[FFT_MAXN],g[FFT_MAXN],t[FFT_MAXN];    //a<->f,b<->g,t<~>c int bitrev[FFT_MAXN]; void fft_init()    //初始化 nw[],bitrev[] 
    {int L=0;while((1<<L)!=FFT_MAXN) L++;for(int i=1;i<FFT_MAXN;i++)  bitrev[i]=bitrev[i>>1]>>1|((i&1)<<(L-1));for(int i=0;i<=FFT_MAXN;i++) nw[i]=cp((db)cosl(2*pi/FFT_MAXN*i),(db)sinl(2*pi/FFT_MAXN*i));}// n已保證是2的整數次冪 // flag=1:DFT |  flag=-1: IDFTvoid dft(cp *a,int n,int flag=1)    {int d=0;while((1<<d)*n!=FFT_MAXN) d++;for(int i=0;i<n;i++) if(i<(bitrev[i]>>d))swap(a[i],a[bitrev[i]>>d]);for(int l=2;l<=n;l<<=1){int del=FFT_MAXN/l*flag;    // 決定 wn是在復平面是順時針還是逆時針變化，以及變化間距 for(int i=0;i<n;i+=l){cp *le=a+i,*ri=a+i+(l>>1);cp *w=flag==1? nw:nw+FFT_MAXN;    // 確定wn的起點 for(int k=0;k<(l>>1);k++){cp ne=*ri * *w;*ri=*le-ne,*le=*le+ne;le++,ri++,w+=del;}}}if(flag!=1) for(int i=0;i<n;i++) a[i].a/=n,a[i].b/=n;}// convo(a,n,b,m,c) a[0..n]*b[0..m] -> c[0..n+m]void convo(LL *a,int n,LL *b,int m,LL *c){for(int i=0;i<=n+m;i++) c[i]=0;int N=2;while(N<=n+m) N<<=1;    // N是c擴展后的長度 for(int i=0;i<N;i++)    //擴展 a[],b[] ，存入f[],g[]，注意取模 
        {LL aa=i<=n?a[i]:0,bb=i<=m? b[i]:0;     aa%=mod,bb%=mod;f[i]=cp(db(aa>>15),db(aa&32767));g[i]=cp(db(bb>>15),db(bb&32767));}dft(f,N),dft(g,N);for(int i=0;i<N;i++)    // 恢復虛部兩個“乘積”（乘積具體意義見上文）
        {int j=i? N-i:0;t[i]=((f[i]+!f[j])*(!g[j]-g[i])+(!f[j]-f[i])*(g[i]+!g[j]))*cp(0,0.25);}dft(t,N,-1);for(int i=0;i<=n+m;i++)    upmo(c[i],(LL(t[i].a+0.5))%mod<<15);for(int i=0;i<N;i++)    // 恢復實部兩個“乘積”
        {int j=i? N-i:0;t[i]=(!f[j]-f[i])*(!g[j]-g[i])*cp(-0.25,0)+cp(0,0.25)*(f[i]+!f[j])*(g[i]+!g[j]);}dft(t,N,-1);for(int i=0;i<=n+m;i++)    upmo(c[i],LL(t[i].a+0.5)+(LL(t[i].b+0.5)%mod<<30));}
}

舉個栗子~　　?hdu 6088 Rikka with Rock-paper-scissors (2017 多校第五場 1004） 【組合數學 + 數論 + 模意義下的FFT】

?

//本博客主要參考資料：數字信號處理——基于計算機的方法（第四版）　　[美] Sanjit K. Mitra 著　　余翔宇 譯

轉載請注明出處?http://www.cnblogs.com/Just--Do--It/p/7892254.html

謝謝閱讀

?