POJ 1811 Prime Test （Rabin-Miller強偽素數測試 和Pollard-rho 因數分解）

題目鏈接

Description

Given a big integer number, you are required to find out whether it's a prime number.

Input

The first line contains the number of test cases T (1 <= T <= 20 ), then the following T lines each contains an integer number N (2 <= N < 254).

Output

For each test case, if N is a prime number, output a line containing the word "Prime", otherwise, output a line containing the smallest prime factor of N.

Sample Input

2
5
10

Sample Output

Prime
2

分析：
給定一個小于2^54的整數，判斷該數是不是素數，如果是素數的話，輸出“Prime”，否則輸出該數的最小的素因子。熟悉的有關素數的算法在這道題看來都還是太弱了，所以得額外的找方法來解決。

應用到的兩個重要算法是Rabin-Miller強偽素數測試和Pollard ?因數分解算法。前者可以在 的時間內以很高的成功概率判斷一個整數是否是素數。后者可以在最優 的時間內完成合數的因數分解。這兩種算法相對于試除法都顯得比較復雜。本文試圖對這兩者進行簡單的闡述，說明它們在32位計算機上限制在64位以內的條件下的實現中的細節。下文提到的所有字母均表示整數。

一、Rabin-Miller強偽素數測試
Rabin-Miller強偽素數測試的基本思想來源于如下的Fermat小定理：
如果p是一個素數，則對任意a有 (a^p)%p=a。特別的，如果p不能整除a，則還有(a^(p-1))%p=1 。
利用Fermat小定理可以得到一個測試合數的有力算法：對n>1，選擇a>1，計算(a^(n-1))%n，若結果不等于1則n是合數。若結果等于1則n可能是素數，并被稱為一個以a為基的弱可能素數（weak probable prime base a，a-PRP）;若n是合數，則又被稱為一個以a為基的偽素數（pseudoprime）。

這個算法的成功率是相當高的。在小于25,000,000,000的1,091,987,405個素數中，一共只用21,853個以2為基的偽素數。但不幸的是，Alford、Granville和Pomerance在1994年證明了存在無窮多個被稱為Carmichael數的整數對于任意與其互素的整數a算法的計算結果都是1。最小的五個Carmichael數是561、1,105、1,729、2,465和2,801。

考慮素數的這樣一個性質：若n是素數，則1對模n的平方根只可能是1和-1 。因此a^(n-1) 對模n的平方根 a^((n-1)/2)也只可能是1和-1 。如果(n-1)/2本身還是一個偶數，我們可以再取一次平方根……將這些寫成一個算法：
（Rabin-Miller強偽素數測試）記n-1=(2^s)d，其中d是奇數而s非負。如果(a^d)%n=1 ，或者對某個 0<=r<s有(a^((2^r)d))%n=-1 ，則認為n通過測試，并稱之為一個以a為基的強可能素數（strong probable prime base a，a-SPRP）。若n是合數，則又稱之為一個以a為基的強偽素數（strong pseudoprime）。

這個測試同時被冠以Miller的名字是因為Miller提出并證明了如下測試：如果擴展黎曼猜想（extended Riemann hypothesis）成立，那么對于所有滿足1<a<2(log n)^2 的基a，n都是a-SPRP，則n是素數。
盡管Monier和Rabin在1980年證明了這個測試的錯誤概率（即合數通過測試的概率）不超過 1/4，單個測試相對來說還是相當弱的（Pomerance、Selfridge和Wagstaff, Jr.證明了對任意a>1都存在無窮多個a-SPRP）。但由于不存在“強Carmichael數”（任何合數n都存在一個基a試之不是a-SPRP），我們可以組合多個測試來產生有力的測試，以至于對足夠小的n可以用來證明其是否素數。

取前k個素數為基，并用 來表示以前k個素數為基的強偽素數，Riesel在1994年給出下表：

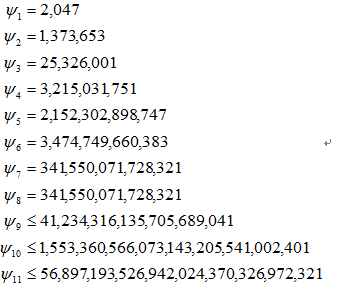
考慮到64位二進制數能表示的范圍，只需取前9個素數為基，則對小于φ8 的所有大于1的整數測試都是正確的；對大于或等于 φ8并小于2^64 的整數測試錯誤的概率不超過1/(2^18) 。

Rabin-Miller強偽素數測試本身的形式稍有一些復雜，在實現時可以下面的簡單形式代替：
對 n>1，如果(a^(n-1))%n=1則認為n通過測試。
代替的理由可簡單證明如下：
仍然記n-1=(2^s)d ，其中d是奇數而s非負。若n是素數，由(a^(n-1))%n=1可以推出(a^(2^(s-1)d))%n=1=(a^((n-1)/2))%n或(a^(2^(s-1)d))%n=-1=(a^((n-1)/2))%n 。若為前者，顯然取r=s-1 即可使n通過測試。若為后者，則繼續取平方根，直到對某個 1<=r<s有 (a^((2^r)d))%n=-1，或(a^(2d))%n=1 。無論 (a^d)%n=1還是 a^d)%n=-1，n都通過測試。

Rabin-Miller強偽素數測試的核心是冪取模（即計算 ）(a^s)%n。計算冪取模有以下的 O(log n)算法（以Sprache偽代碼語言描述）：
這個算法在32位計算機上實現的難點在于指令集和絕大部分編程語言的編譯器都只提供了32位相乘結果為64位的整數乘法，浮點運算由于精度的問題不能應用于這里的乘法。唯一解決辦法是模仿一些編譯器內建的64位整數乘法來實現兩個無符號64位相乘結果為128位的乘法。這個乘法可以將兩個乘數分別分割成兩個32位數來實現。為方便乘法之后的取模運算，運算結果應當用連續的128個二進制位來表示。以下是其偽代碼：

乘法之后的取模運算可以用浮點運算快速完成。具體做法是乘積的高64位和低64位分別先對除數取模，然后再利用浮點單元合并取模。這里的浮點運算要求浮點單元以最高精度運算，計算前應先將浮點單元控制字中的精度控制位設置為64位精度。為保證精度，應當用80位浮點數實現此運算。偽代碼如下：

至此，Rabin-Miller強偽素數測試的核心已經全部實現。

二、Pollard-rho 因數分解算法
Pollard-rho因數分解算法又稱為Pollard Monte Carlo因數分解算法。它的核心思想是：選取一個隨機數a。再選一個隨機數b。檢查 gcd(a-b,n)是否大于1。若大于1， gcd(a-b,n)就是n的一個因子。若不大于1，再選取隨機數c，檢查 gcd(c-b,n)和 gcd(c-a,n)。如此繼續，直到找到n的一個非平凡因子。

代碼：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <time.h>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll __int64//****************************************************************
// Miller_Rabin 算法進行素數測試
//速度快，而且可以判斷 <2^63的數
//****************************************************************
const int S=20;//隨機算法判定次數，S越大，判錯概率越小//計算 (a*b)%c.   a,b都是long long的數，直接相乘可能溢出的
/*
ll Mult_mod (ll a,ll b,ll c)   //  a,b,c <2^63
{a%=c;b%=c;ll ret=0;while (b){if (b&1) {ret+=a;ret%=c;}a<<=1;if (a>=c)a%=c;b>>=1;}return ret;
}*/ll Mult_mod (ll a,ll b,ll c)  //減法實現比取模速度快
{//返回(a*b) mod c,a,b,c<2^63a%=c;b%=c;ll ret=0;while (b){if (b&1){ret+=a;if (ret>=c) ret-=c;}a<<=1;if (a>=c) a-=c;b>>=1;}return ret;
}//計算  x^n %c
ll Pow_mod (ll x,ll n,ll mod) //x^n%c
{if (n==1) return x%mod;x%=mod;ll tmp=x;ll ret=1;while (n){if (n&1) ret=Mult_mod(ret,tmp,mod);//(a*b)%ctmp=Mult_mod(tmp,tmp,mod);n>>=1;}return ret;
}//以a為基,n-1=x*2^t      a^(n-1)=1(mod n)  驗證n是不是合數
//一定是合數返回true,不一定返回false
bool Check (ll a,ll n,ll x,ll t)
{ll ret=Pow_mod(a,x,n);//(a^x)%nll last=ret;for (int i=1; i<=t; i++){ret=Mult_mod(ret,ret,n);if(ret==1&&last!=1&&last!=n-1) return true; //合數last=ret;}if (ret!=1) return true;return false;
}// Miller_Rabin()算法素數判定
//是素數返回true.(可能是偽素數，但概率極小)
//合數返回false;bool Miller_Rabin (ll n)
{if (n<2) return false;if (n==2) return true;if ((n&1)==0) return false;//偶數ll x=n-1;ll t=0;while ((x&1)==0)//不斷的對于x進行右移操作{x>>=1;t++;}for (int i=0; i<S; i++){ll a=rand()%(n-1)+1; //rand()需要stdlib.h頭文件if (Check(a,n,x,t))return false;//合數}return true;
}//************************************************
//pollard_rho 算法進行質因數分解
//************************************************ll factor[100];//質因數分解結果（剛返回時是無序的）
int tol;//質因數的個數。數組下標從0開始ll Gcd (ll a,ll b)
{if (a==0) return 1;   if (a<0) return Gcd(-a,b);while (b){ll t=a%b;a=b;b=t;}return a;
}ll Pollard_rho (ll x,ll c)
{ll i=1,k=2;ll x0=rand()%x;ll y=x0;while (true){i++;x0=(Mult_mod(x0,x0,x)+c)%x;ll d=Gcd(y-x0,x);if (d!=1 && d!=x) return d;if (y==x0) return x;if (i==k){y=x0;k+=k;}}
}
//對n進行素因子分解
void Findfac (ll n)
{if (Miller_Rabin(n)) //素數{factor[tol++]=n;return;}ll p=n;while (p>=n) p=Pollard_rho(p,rand()%(n-1)+1);Findfac(p);Findfac(n/p);
}int main ()  // Poj 1811 交G++ 比c++ 快很多
{// srand(time(NULL));//需要time.h頭文件  //POJ上G++要去掉這句話int T;scanf("%d",&T);while (T--){ll n;scanf("%I64d",&n);if (Miller_Rabin(n)){printf("Prime\n");continue;}tol=0;Findfac(n);ll ans=factor[0];for (int i=1; i<tol; i++)if (factor[i]<ans)ans=factor[i];printf("%I64d\n",ans);}return 0;
}