題目描述
a180285非常喜歡滑雪。他來到一座雪山,這里分布著M條供滑行的軌道和N個軌道之間的交點(同時也是景點),而且每個景點都有一編號i(1≤i≤N)和一高度Hi?。a180285能從景點ii滑到景點j當且僅當存在一條i和j之間的邊,且i的高度不小于j。 與其他滑雪愛好者不同,a180285喜歡用最短的滑行路徑去訪問盡量多的景點。如果僅僅訪問一條路徑上的景點,他會覺得數量太少。于是a180285拿出了他隨身攜帶的時間膠囊。這是一種很神奇的藥物,吃下之后可以立即回到上個經過的景點(不用移動也不被認為是a180285 滑行的距離)。請注意,這種神奇的藥物是可以連續食用的,即能夠回到較長時間之前到過的景點(比如上上個經過的景點和上上上個經過的景點)。 現在,a180285站在11號景點望著山下的目標,心潮澎湃。他十分想知道在不考慮時間膠囊消耗的情況下,以最短滑行距離滑到盡量多的景點的方案(即滿足經過景點數最大的前提下使得滑行總距離最小)。你能幫他求出最短距離和景點數嗎?
輸入格式:
輸入的第一行是兩個整數N,M。
接下來1行有N個整數Hi?,分別表示每個景點的高度。
接下來M行,表示各個景點之間軌道分布的情況。每行3個整數Ui?,Vi?,Ki?。表示編號為Ui?的景點和編號為Vi?的景點之間有一條長度為Ki?的軌道。
輸出格式:
輸出一行,表示a180285最多能到達多少個景點,以及此時最短的滑行距離總和。
題解:
對于高度不同的兩點,他們之間的邊是有向的,對于同于高度的點,有邊就可以互相到達,我們只需要選取最短的一些邊使他們仍聯通即可。
若按照正常思路,以邊權排序,直接跑Kruskal的話,會發現可能出現有下面的點連接上面的點,如:他會直接選取兩條邊權為5的邊
?
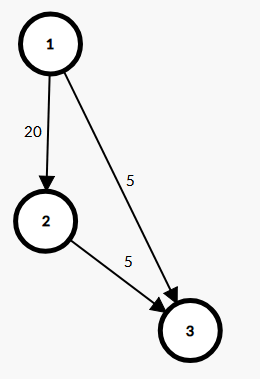
?
?我們考慮如何消除高度的影響,我們以終點高度為第一關鍵字,邊權為第二關鍵字排序,那么就不可能出現上面的情況,因為他會先選20的邊。
相當于選點是逐層進行的,上面的點一定會先被選取,所以這個點選了之后,不可能再連一條向上的邊。
接著愉快地打出了代碼。


#include<bits/stdc++.h> using namespace std; #define ll long longconst int maxn=1000005; int n,m; ll ans; int fa[maxn],h[maxn]; struct edge{int x,y;ll k; }a[maxn];template<class T>inline void read(T &x){x=0;char ch=getchar();while(!isdigit(ch)) ch=getchar();while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} }void swap(ll &x,ll &y){ll t=x;x=y;y=t;}bool cmp(edge a,edge b){if(h[a.y]==h[b.y]) return a.k<b.k;return h[a.y]>h[b.y]; }int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]); }void kruskal(){sort(a+1,a+m+1,cmp);int k=0;for(int i=1;i<=m;i++){int dx=find(a[i].x),dy=find(a[i].y);if(dx!=dy){fa[dx]=dy;ans+=a[i].k;k++;}if(k==n-1) break;;}printf("%d %lld",k+1,ans); }int main(){read(n);read(m);for(int i=1;i<=n;i++) read(h[i]),fa[i]=i;for(int i=1;i<=m;i++){int x,y,z;read(x);read(y);read(z);if(h[x]<h[y]) swap(x,y);a[i]=(edge){x,y,z};}kruskal(); }
然后。。。。。

我們會發現是什么沒考慮到呢?接著便可以發現可能有出發點達不到的地方,這些地方是沒用的。
那么就可以考慮記錄1可以利用的邊,用這些邊跑Kruskal。在最初讀入時對于高度不同的點建有向邊,
高度相同建雙向邊,跑一邊dfs,要判斷是否遍歷過。


#include<bits/stdc++.h> using namespace std; #define ll long longconst int maxn=1000005; int n,m,_n=1,cnt; ll ans; int fa[maxn],h[maxn]; bool vis[maxn]; vector<pair<int,ll> >e[maxn]; struct edge{int x,y;ll k; }a[maxn];template<class T>inline void read(T &x){x=0;char ch=getchar();while(!isdigit(ch)) ch=getchar();while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} }void swap(ll &x,ll &y){ll t=x;x=y;y=t;}bool cmp(edge a,edge b){if(h[a.y]==h[b.y]) return a.k<b.k;return h[a.y]>h[b.y]; }int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]); }void kruskal(){sort(a+1,a+cnt+1,cmp);int k=0;for(int i=1;i<=cnt;i++){int dx=find(a[i].x),dy=find(a[i].y);if(dx!=dy){fa[dx]=dy;ans+=a[i].k;k++;}if(k==_n-1) break;}printf("%d %lld",_n,ans); }void dfs(int u,int f){for(unsigned int i=0;i<e[u].size();i++){int v=e[u][i].first;if(v==f) continue;a[++cnt]=(edge){u,v,e[u][i].second};if(!vis[v]){vis[v]=true;_n++;dfs(v,u);}} }int main(){read(n);read(m);for(int i=1;i<=n;i++) read(h[i]),fa[i]=i;for(int i=1;i<=m;i++){int x,y,z;read(x);read(y);read(z);if(h[x]<h[y]) swap(x,y);e[x].push_back(make_pair(y,z));if(h[x]==h[y]) e[y].push_back(make_pair(x,z));}vis[1]=true;dfs(1,0);kruskal(); }
?
)





)












)