淺談Aho-Corasick automaton(AC自動機)

Aho-Corasick automaton是什么？

要學會AC自動機，我們必須知道什么是Trie，也就是字典樹。Trie樹，又稱單詞查找樹或鍵樹，是一種樹形結構，是一種哈希樹的變種。典型應用是用于統計和排序大量的字符串（但不僅限于字符串），所以經常被搜索引擎系統用于文本詞頻統計。

首先我們要知道trie，而且要知道KMP，這樣就可以學AC自動機了!

其實AC自動機就是trie和KMP的結合體。主要構建trie后使用KMP的主導思想構建fail邊，每次匹配與KMP相似。

下面我們看看如何構造fail邊。

fail邊就是類似KMP中的next數組，在失配的時候能夠指向的地方。

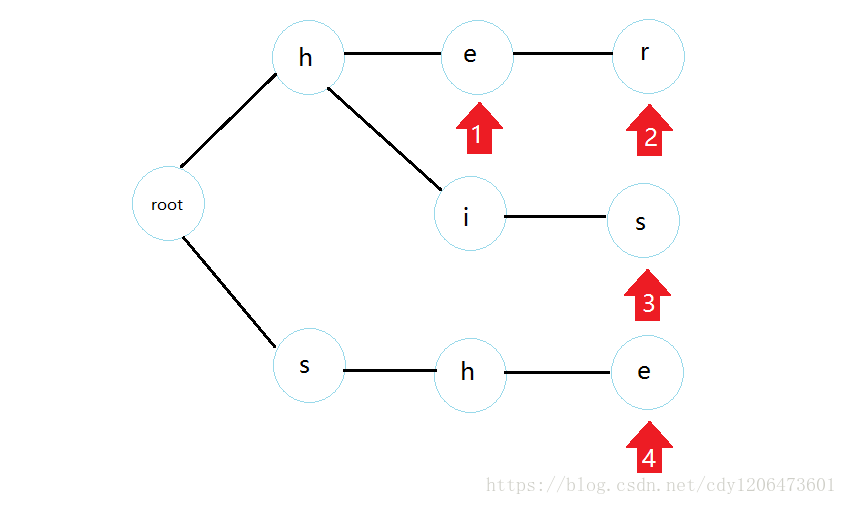
這就是一顆trie樹，那么我們應該怎么去連fail邊呢？

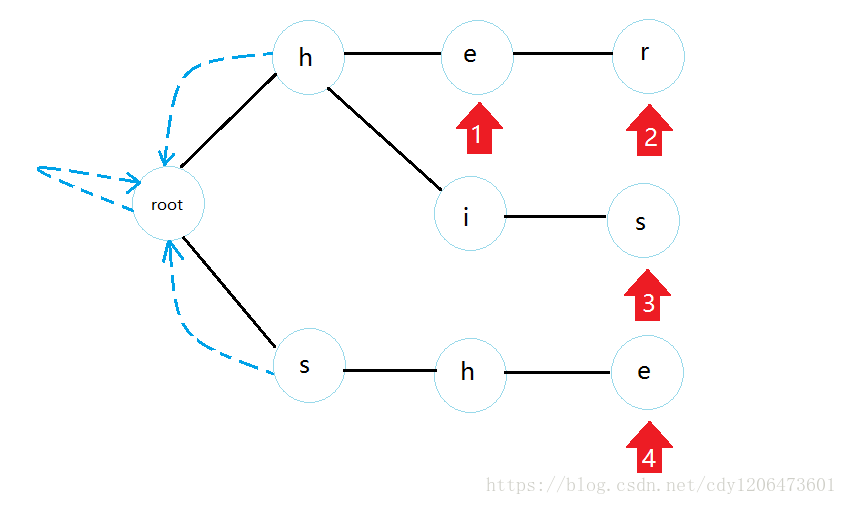
首先我們知道root的fail邊是連向自己的，而且所有與root直接相連的點fail都指向root。

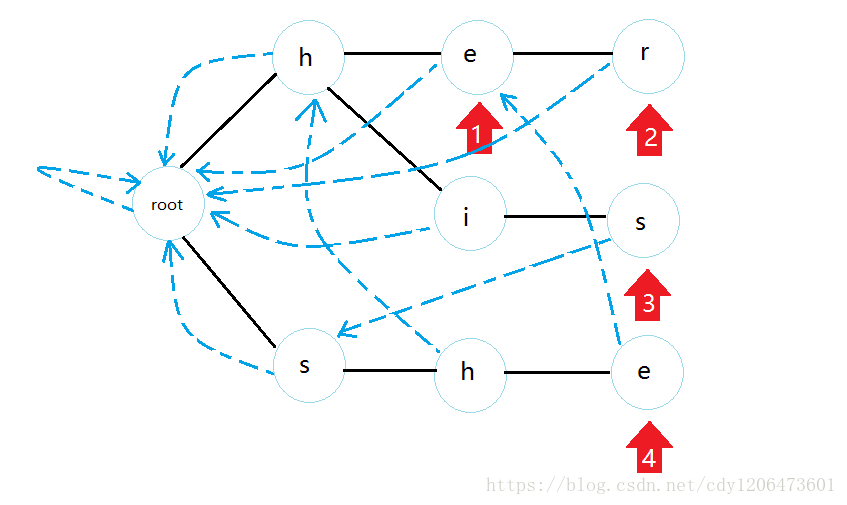
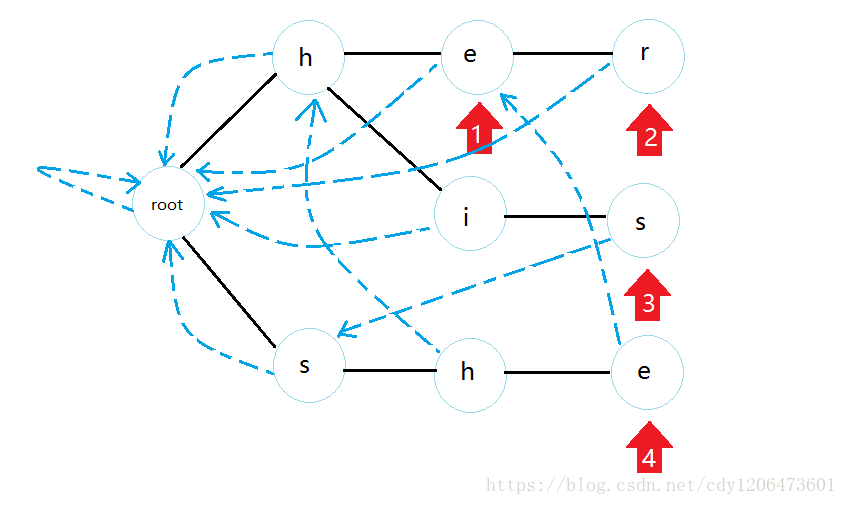
然后每個點，看看自己父親的fail邊指向的位置的點是否有一個與它長的一樣的兒子，如果有，那么連上，否則繼續找fail邊，直到root為止(注意這個過程我們用bfs實現)。所以最終連完的fail邊就是這樣：

這樣我們只需要每一位去匹配就好了。

有人問，怎么匹配：

舉個栗子：
用上面的圖：

假設原串是：ahershe，這棵trie上有his,her,he,she。
我們從root開始，先查找root點有沒有當前字母的兒子a，有那么指針x指到h點上，這樣一直匹配；如果沒有，那么就直接跳到當前點的fail邊上，這樣保證前面匹配的全都是相同的，直到有這樣的兒子或者已經到了root并且沒有這樣的兒子為止。
注意每跳一個點就必須從當前點遍歷一遍它的fail邊直到root的邊集，就是說沿著fail邊跳一直到root為止，這是為了避免當前點沒有被標記，但是在它fail邊到達root的路徑上有被標記的點。

Exanple

【GDOI2013模擬4】貼瓷磚

Description

A鎮的主街是由N個小寫字母構成，鎮長準備在上面貼瓷磚，瓷磚一共有M種，第i種上面有Li個小寫字母，瓷磚不能旋轉也不能被分割開來，瓷磚只能貼在跟它身上的字母完全一樣的地方，允許瓷磚重疊，并且同一種瓷磚的數量是無窮的。
問街道有多少字母(地方)不能被瓷磚覆蓋。

Input

第一行輸入街道長度N(1<=N<=300,000)。
第二行輸入N個英文小寫字母描述街道的情況。
第三行輸入M(1<=M<=5000)，表示瓷磚的種類。
接下來M行，每行描述一種瓷磚，長度為Li(1<=Li<=5000)，全部由小寫字母構成。

Output

輸出有多少個地方不能被瓷磚覆蓋。

Sample Input

輸入1：

6

abcbab

2

cb

cbab

輸入2：

4

abab

2

bac

baba

輸入3：

6

abcabc

2

abca

cab

Sample Output

輸出1：

2

輸出2：

4

輸出3：

1

Data Constraint

N(1<=N<=300,000)

Solution

我們把原字符串每一位都進行匹配，然后首先預處理出trie中每一個點對應所有fail邊中最大的長度，然后匹配的時候記錄下每一位中能夠覆蓋到的最大長度，最后用線段樹維護(當然你可以直接用差分約束)。

Code

#include<cstdio>
#include<iostream>
#include<cstring>
#define mo 1000010
using namespace std;
struct Moon{int fail,num,maxl;}point[4000010];
int son[4000010][27];
int lengt_max[300010],length[300010];
char s[300010],ch[300010];
int len,n,root,sz; 
int d[mo];
int f[300010*4],tag[300010*4];
void make_trie(char s1[300010],int len1,int t,int x,int id)
{if(t>len1) {point[x].num=id;point[x].maxl=length[id];return;}   if(!son[x][s1[t]-96]){son[x][s1[t]-96]=++sz;++son[x][0];make_trie(s1,len1,t+1,sz,id);   }else make_trie(s1,len1,t+1,son[x][s1[t]-96],id);
}
void build_fail()
{int i,x,k,head=0,tail=0;for (i=1;i<=26&&tail<son[root][0];++i)if(son[root][i]) {d[++tail]=son[root][i];point[son[root][i]].fail=root;}while(head!=tail){head=head%mo+1;x=d[head];if(!son[x][0]) continue;for (i=1;i<=26;++i)if(son[x][i]){tail=tail%mo+1;d[tail]=son[x][i];k=point[x].fail;while(k!=root){if(son[k][i]) break;k=point[k].fail;if(k==root&&!son[k][i]) break;}if(son[k][i]) point[son[x][i]].fail=son[k][i];else point[son[x][i]].fail=root;point[son[x][i]].maxl=max(point[son[x][i]].maxl,point[point[son[x][i]].fail].maxl);}}
}
void Check()
{int x=root,k;for (int i=1;i<=len;){if(son[x][s[i]-96]) {x=son[x][s[i]-96];  lengt_max[i]=max(lengt_max[i],point[x].maxl);++i;}   else x=point[x].fail;if(x==root&&!son[x][s[i]-96]) ++i;}
} 
void change(int v,int l,int r,int x,int y)
{if(l==x&&r==y){tag[v]=1;f[v]=r-l+1; return;}int mid=(l+r)/2;if(tag[v]){tag[v*2]=1,f[v*2]=mid-l+1;tag[v*2+1]=1,f[v*2+1]=r-mid;tag[v]=0;}if(y<=mid) change(v*2,l,mid,x,y);else if(x>mid) change(v*2+1,mid+1,r,x,y);else change(v*2,l,mid,x,mid),change(v*2+1,mid+1,r,mid+1,y);f[v]=f[v*2]+f[v*2+1];
}
int main()
{scanf("%d",&len);scanf("%s",s+1);scanf("%d",&n);int i,j;root=sz=point[1].fail=1;for (i=1;i<=n;++i){scanf("%s",ch+1);length[i]=strlen(ch+1);make_trie(ch,length[i],1,root,i);}build_fail();Check();for (i=1;i<=len;++i) if(lengt_max[i]) change(1,1,len,i-lengt_max[i]+1,i);printf("%d\n",len-f[1]);
}