自編碼器（AutoEncoder），也稱自編碼模型，是一種基于無監督學習的數據維度壓縮和特征表示方法，目的是對一組數據學習出一種表示。1986年 Rumelhart 提出自編碼模型用于高維復雜數據的降維。由于自動編碼器通常應用于無監督學習，所以不需要對訓練樣本進行標記。自動編碼器在圖像重構、聚類、降維、自然語言翻譯等方面應用廣泛。

1. 數據表示

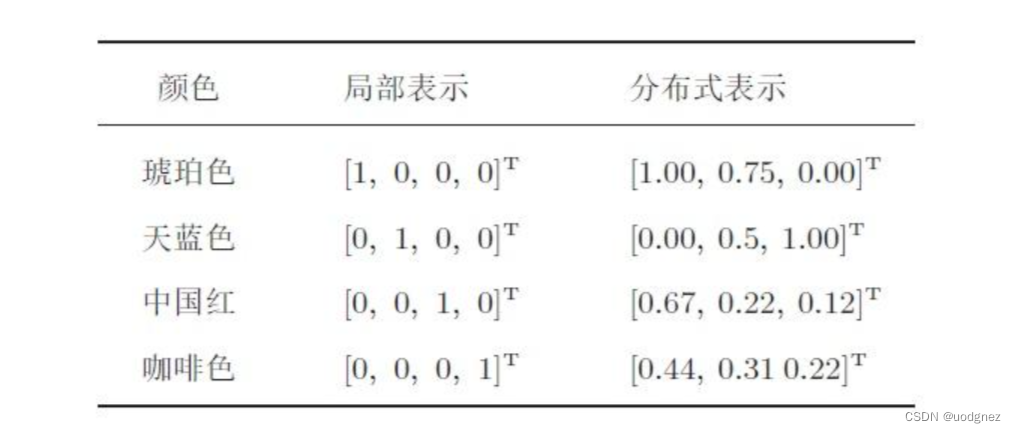
數據表示（Data Representation）是使用另一種形式呈現原始數據的方法，這一技術也被稱為隱式表示（Latent Representation）或者轉碼（Coding）。

• 原始數據為 $[2,4,6,8,10]$：
  我們可以使用文字以2開頭，以10結尾的偶數列來表示該原始數據，也可以使用 $[x,2x,3x,4x,5x]$ 且 $x=2$ 來表示該原始數據。
• 原始數據為 ${[}^{\prime }蘋{果}^{\prime }{,}^{\prime }{梨}^{\prime }{,}^{\prime }百香{果}^{\prime }]$：
  我們可以使用序列 $[0,1,2]$ 來表示該原始數據，也可以使用水果這一概括性的詞匯來表示原始數據。

很顯然，一個數據的數據表示并不是唯一的，且這種表示可以是精確的、也可以是有些模糊的，甚至可以看起來與原始數據毫不相關，但無論如何，數據表示的結果必須攜帶原始數據上大部分的信息。廣義地表示，只要數據B是以另一種形式呈現數據A、并且數據B上攜帶數據A大部分的信息，我們就可以說B是A的數據表示。同時，“另一種形式”既可以是文字-數字這樣不同類別的數據之間的形式差異，也可以是數字-數字這樣相同類別，但不同大小、不同數量的數據之間的形式差異。在實際計算當中，當數據B是數據A的數據表示時，數據B通常是從數據A總結出的規律、或直接在數據A上計算得出的新數據。

根據以上數據表示的廣義定義可以得知，我們非常熟悉的數據編碼（獨熱編碼、順序編碼等操作）、特征提取、升維降維、Embedding等方法都可以囊括到數據表示領域當中。在這領域當中，使用機器學習或深度學習手段令算法自己求解出數據表示結果的領域被稱之為表征學習。自編碼器是表征學習中極具特色的代表架構。為了實現數據表示的功能，自編碼器能夠“接收數據A，并輸出另一種形式的數據B”，因此自編碼器是為“生產新數據”而生的架構。

2. 自編碼器模型簡介

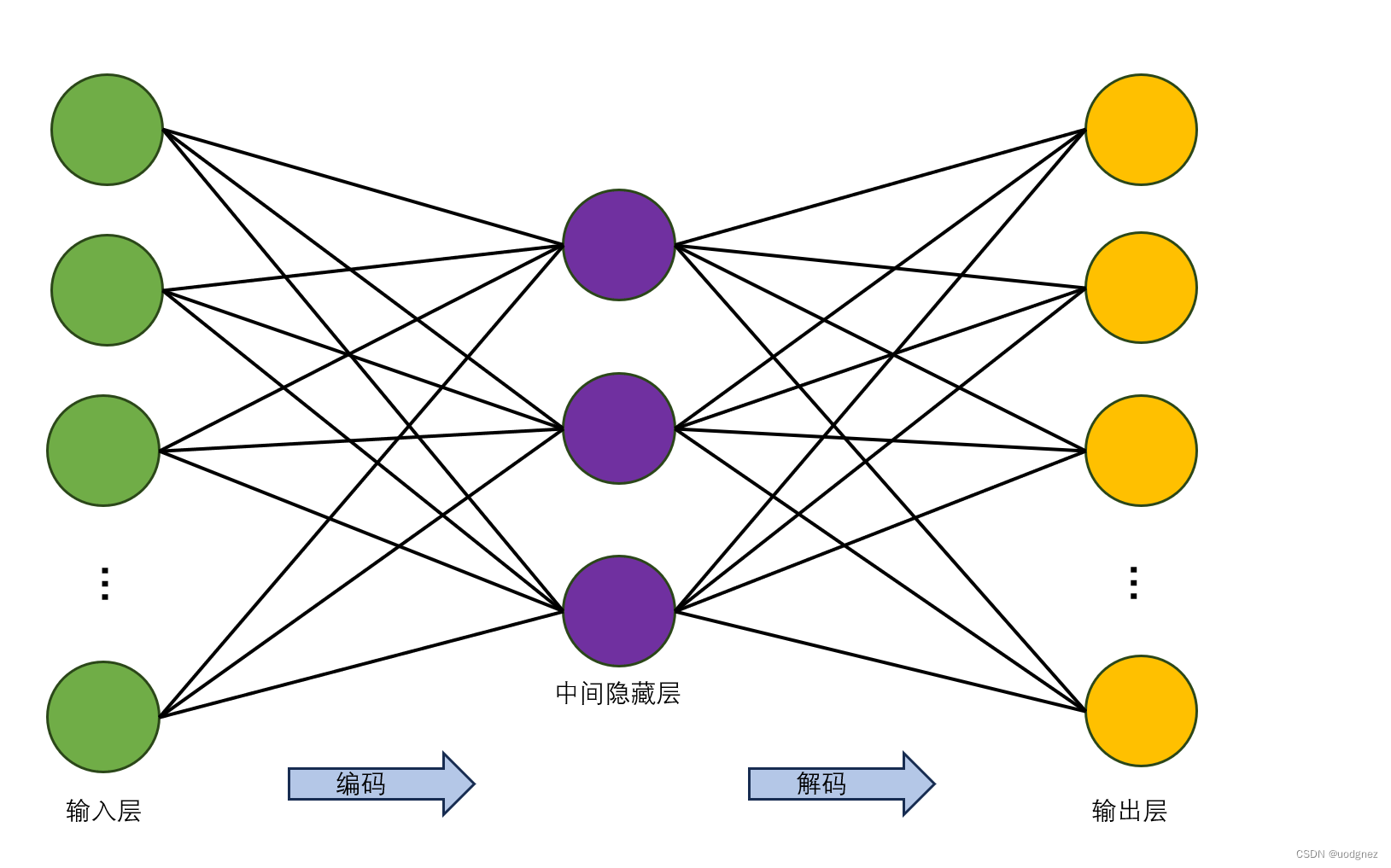
最初的自編碼器是一個三層網絡結構，即輸入層、中間隱藏層以及輸出層，其中輸入層和輸出層的神經元個數相同。如下圖所示：

深度自編碼器是將自編碼器堆積起來，可以包含多個中間隱藏層。由于其可以有更多的中間隱藏層，所以對數據的表示和編碼能力更強，而且在實際應用中也更加常用。如下圖所示：

稀疏自編碼器，是在原有自編碼器的基礎上，對隱層單元施加稀疏性約束，這樣會得到對輸入數據更加緊湊的表示，在網絡中僅有小部分神經元會被激活。常用的稀疏約束是使用 $\text{L1}$ 范數約束，目的是讓不重要的神經元的權重為0。

卷積自編碼器是使用卷積層搭建獲得的自編碼網絡。當輸入數據為圖像時，由于卷積操作可以從圖像數據中獲取更豐富的信息，所以使用卷積層作為自編碼器隱藏層，通常可以對圖像數據進行更好的表示。在實際應用中，用于處理圖像的自動編碼器的隱藏層幾乎都是基于卷積的自編碼器。在卷積自編碼器的編碼器部分，通常可以通過池化層負責對數據進行下采樣，卷積層負責對數據進行表示，而解碼器則通常使用可以對特征映射進行上采樣的操作來完成。