智能優化算法之粒子群模型(含python案例代碼)

粒子群優化模型概述

????????粒子群優化（Particle Swarm Optimization，簡稱PSO）是一種基于群體智能的優化算法，最早由美國社會心理學家James Kennedy和Russell Eberhart于1995年提出。PSO的靈感來自鳥群和魚群等自然界群體行為的觀察。

????????PSO的基本思想是通過模擬群體中個體的協作和信息共享來尋找問題的最優解。在PSO中，個體被稱為“粒子”，每個粒子代表搜索空間中的一個潛在解。這些粒子通過在搜索空間中移動來尋找最優解，其移動的方向和速度受到個體經驗和群體經驗的影響。

PSO的基本模型

粒子表示： 每個粒子都有一個位置向量和一個速度向量，它們分別表示在搜索空間中的當前位置和移動的速度。
適應度函數： 問題的目標函數被定義為適應度函數，粒子的目標是最小化或最大化這個適應度函數。
個體最優解： 每個粒子都會記住自己在搜索空間中找到的最好位置，稱為個體最優解。
全局最優解： 在整個粒子群中，會有一個粒子記住全局最優解，即整個群體中適應度最好的位置。
更新規則： 粒子根據一定的更新規則（通常包括個體經驗和群體經驗）來調整自己的位置和速度。

更新規則的一般形式為：

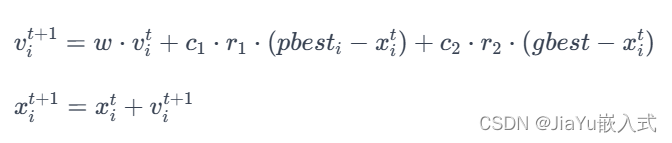
其中：

????????這個算法在不同問題上取得了很好的效果，特別是在連續優化問題中。在使用PSO時，需要根據具體問題來調整算法的參數，例如粒子數目、學習因子、慣性權重等。

什么時候用粒子群優化？

????????粒子群優化（Particle Swarm Optimization，PSO）是一種用于求解優化問題的群體智能算法。PSO適用于多種優化問題，但其特定的優點和適用場景使得它在某些情況下更為合適。

????????連續優化問題： PSO主要用于求解連續優化問題，其中目標函數是連續可導的。這包括了許多工程和科學應用，如機器學習模型的參數優化、神經網絡權重的調整、信號處理、控制系統設計等。

????????無約束問題： PSO對問題的約束較為寬松，因此適用于無約束優化問題。如果問題具有復雜的約束條件，可能需要對PSO進行改進或選擇其他更適合處理約束問題的優化算法。

????????高維空間： PSO在高維搜索空間中表現良好。對于具有大量變量的問題，PSO能夠有效地探索搜索空間，找到全局最優解。

????????全局優化： PSO的群體協作機制使其對全局優化問題具有較好的收斂性。它有助于避免陷入局部最優解，尤其在搜索空間復雜或存在多個局部最優解的情況下。

????????簡單實現： PSO的實現相對簡單，不需要太多的參數調整。這使得它成為一種易于使用和理解的優化算法，特別適用于初學者或對算法細節不太敏感的應用場景。

????????動態環境： PSO對于動態環境中的優化問題具有較好的適應性。由于其實時更新的特性，PSO能夠快速適應目標函數或搜索空間的變化。

????????盡管PSO在許多情況下表現良好，但在某些問題上可能不如其他優化算法，因此在選擇優化算法時，應根據具體問題的特性、算法的優點和缺點做出合理的選擇。

案例代碼1

????????以下是一個簡單的粒子群優化算法的 Python 示例代碼。這個例子是一個簡單的單變量優化問題，目標是最小化函數f(x)=x^2+5.

import random# 粒子群優化算法
def particle_swarm_optimization(obj_func, num_particles, num_iterations):# 初始化粒子群particles = [{'position': random.uniform(-10, 10),'velocity': random.uniform(-1, 1),'pbest_position': 0,'pbest_value': float('inf')} for _ in range(num_particles)]# 尋找全局最優解的粒子gbest_particle = min(particles, key=lambda p: obj_func(p['position']))# PSO參數inertia_weight = 0.5cognitive_coefficient = 1.5social_coefficient = 1.5# 開始優化迭代for _ in range(num_iterations):for particle in particles:# 更新速度和位置r1, r2 = random.uniform(0, 1), random.uniform(0, 1)particle['velocity'] = (inertia_weight * particle['velocity'] +cognitive_coefficient * r1 * (particle['pbest_position'] - particle['position']) +social_coefficient * r2 * (gbest_particle['pbest_position'] - particle['position']))particle['position'] += particle['velocity']# 更新個體最優解current_value = obj_func(particle['position'])if current_value < particle['pbest_value']:particle['pbest_value'] = current_valueparticle['pbest_position'] = particle['position']# 更新全局最優解if current_value < gbest_particle['pbest_value']:gbest_particle = {'pbest_position': particle['pbest_position'],'pbest_value': particle['pbest_value']}return gbest_particle['pbest_position']# 示例問題：最小化函數 f(x) = x^2 + 5
def objective_function(x):return x**2 + 5# 運行粒子群優化算法
best_solution = particle_swarm_optimization(objective_function, num_particles=30, num_iterations=100)# 打印結果
print("最優解：", best_solution)
print("最優解對應的目標函數值：", objective_function(best_solution))

????????這只是一個簡單的示例，實際應用中可能需要根據問題的復雜性進行更多的調整和改進。在實際問題中，需要調整粒子數量、迭代次數、參數等來獲得更好的性能。

案例代碼2

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Ddef fit_fun(x):  # 適應函數return sum(100.0 * (x[0][1:] - x[0][:-1] ** 2.0) ** 2.0 + (1 - x[0][:-1]) ** 2.0)class Particle:# 初始化def __init__(self, x_max, max_vel, dim):self.__pos = np.random.uniform(-x_max, x_max, (1, dim))  # 粒子的位置self.__vel = np.random.uniform(-max_vel, max_vel, (1, dim))  # 粒子的速度self.__bestPos = np.zeros((1, dim))  # 粒子最好的位置self.__fitnessValue = fit_fun(self.__pos)  # 適應度函數值def set_pos(self, value):self.__pos = valuedef get_pos(self):return self.__posdef set_best_pos(self, value):self.__bestPos = valuedef get_best_pos(self):return self.__bestPosdef set_vel(self, value):self.__vel = valuedef get_vel(self):return self.__veldef set_fitness_value(self, value):self.__fitnessValue = valuedef get_fitness_value(self):return self.__fitnessValueclass PSO:def __init__(self, dim, size, iter_num, x_max, max_vel, tol, best_fitness_value=float('Inf'), C1=2, C2=2, W=1):self.C1 = C1self.C2 = C2self.W = Wself.dim = dim  # 粒子的維度self.size = size  # 粒子個數self.iter_num = iter_num  # 迭代次數self.x_max = x_maxself.max_vel = max_vel  # 粒子最大速度self.tol = tol  # 截至條件self.best_fitness_value = best_fitness_valueself.best_position = np.zeros((1, dim))  # 種群最優位置self.fitness_val_list = []  # 每次迭代最優適應值# 對種群進行初始化self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]def set_bestFitnessValue(self, value):self.best_fitness_value = valuedef get_bestFitnessValue(self):return self.best_fitness_valuedef set_bestPosition(self, value):self.best_position = valuedef get_bestPosition(self):return self.best_position# 更新速度def update_vel(self, part):vel_value = self.W * part.get_vel() + self.C1 * np.random.rand() * (part.get_best_pos() - part.get_pos()) \+ self.C2 * np.random.rand() * (self.get_bestPosition() - part.get_pos())vel_value[vel_value > self.max_vel] = self.max_velvel_value[vel_value < -self.max_vel] = -self.max_velpart.set_vel(vel_value)# 更新位置def update_pos(self, part):pos_value = part.get_pos() + part.get_vel()part.set_pos(pos_value)value = fit_fun(part.get_pos())if value < part.get_fitness_value():part.set_fitness_value(value)part.set_best_pos(pos_value)if value < self.get_bestFitnessValue():self.set_bestFitnessValue(value)self.set_bestPosition(pos_value)def update_ndim(self):for i in range(self.iter_num):for part in self.Particle_list:self.update_vel(part)  # 更新速度self.update_pos(part)  # 更新位置self.fitness_val_list.append(self.get_bestFitnessValue())  # 每次迭代完把當前的最優適應度存到列表print('第{}次最佳適應值為{}'.format(i, self.get_bestFitnessValue()))if self.get_bestFitnessValue() < self.tol:breakreturn self.fitness_val_list, self.get_bestPosition()if __name__ == '__main__':# test 香蕉函數pso = PSO(4, 5, 10000, 30, 60, 1e-4, C1=2, C2=2, W=1)fit_var_list, best_pos = pso.update_ndim()print("最優位置:" + str(best_pos))print("最優解:" + str(fit_var_list[-1]))plt.plot(range(len(fit_var_list)), fit_var_list, alpha=0.5)