引言

本文給出了Kalman Filter（卡爾曼濾波）、Extended Kalman Filter（擴展卡爾曼濾波）、Unscented Kalman Filter（無跡卡爾曼濾波）和Asynchronous Filter（異步濾波）的原理及其Matlab代碼。不同的濾波算法以函數形式在不同的m文件，調用即可使用。

Kalman濾波

該部分展示了kalman濾波的代碼及其仿真結果。
狀態轉移模型：
$x(t+1)=Ax(t)+\Gamma w(t)$
其中$x(t)\in R^{n?1}$表示t時刻的狀態向量，$A\in R^{m?m}$是狀態轉移矩陣,Γ是噪聲系數矩陣，w(t)是t時刻的過程噪聲向量, 其為零均值高斯白噪聲，協方差陣為Q>0。
量測模型：
$yi(t)=Hix(t)+vi(t)$
,其中$yi(t)$表示t時刻傳感器網絡中的傳感器i的量測向量，$Hi\in R^{l?m}$是觀測矩陣,vi(t)是t時刻的量測噪聲向量，其為零均值高斯白噪聲，協方差陣為Ri>0。
初始化:


狀態更新:

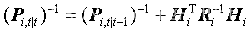
代碼及其結果展示

核心代碼：（完整代碼見文末）

function [estimate, cov_error_estimate] = kalman_filter(measure, x_last,...P_last,flag)
%kalman_filter 基本kalman濾波算法
%   輸入：量測值，上一時刻估計，上一時刻估計誤差協方差,是否預測的標志
%   輸出：當前時刻估計，當前時刻估計誤差協方差
% 當flag為1，則跳過預測步驟
%%
% 狀態轉移矩陣
global A;
% 系統噪聲系數矩陣
global gama;
% 系統噪聲協方差
global Q;
% 量測矩陣
global H;
% 量測噪聲協方差
global R;
%%
% 如果全零，即無初始化
if ~any(x_last)if measure==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0時刻，則取量測值對應的狀態為當前時刻估計，9倍的量測誤%差協方差陣為當前時刻估計誤差協方差。estimate = H\measure;cov_error_estimate = H\(2*(R))/H';end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endif measure==0estimate=forecast;cov_error_estimate = P_forecast;elsekalman_gain = P_forecast*H'/(H*P_forecast*H'+R);estimate = forecast + kalman_gain*(measure - H*forecast);cov_error_estimate = P_forecast - kalman_gain*H*P_forecast;end
end
end

結果展示：

擴展Kalman濾波

擴展卡爾曼濾波是標準卡爾曼濾波在非線性情形下的一種擴展形式，EKF算法是將非線性函數進行泰勒展開，省略高階項，保留展開項的一階項，以此來實現非線性函數線性化，最后通過卡爾曼濾波算法近似計算系統的狀態估計值和方差估計值,對信號進行濾波。
狀態轉移方程與量測方程

泰勒線性化


預測步驟

估計步驟

代碼及其結果展示

核心代碼：（完整代碼見文末）

function [estimate, cov_error_estimate] = extend_kf(measure, x_last, P_last,...flag,radar)
%kalman_filter 擴展kalman濾波算法
%   輸入：量測值，上一時刻估計，上一時刻估計誤差協方差,是否預測的標志,
%雷達的狀態信息
%   輸出：當前時刻估計，當前時刻估計誤差協方差
% 當flag為1，則跳過預測步驟
%%
% 狀態轉移矩陣
global A;
% 系統噪聲系數矩陣
global gama;
% 系統噪聲協方差
global Q;
% 量測噪聲協方差
global R;
%%
% 如果全零，即無初始化
if ~any(x_last)if measure==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0時刻，則取量測值對應的狀態為當前時刻估計，9倍的量測誤%差協方差陣為當前時刻估計誤差協方差。%   此處為9的原因是3倍的標準差為百分之95的可能的誤差值，可以認為%包含了最大誤差的情況。estimate=[radar(1,1)+measure(1,1)*cos(measure(3,1))*cos(measure(2,1));radar(2,1)+measure(1,1)*sin(measure(3,1));radar(3,1)-measure(1,1)*cos(measure(3,1))*sin(measure(2,1));0;0;0];cov_error_estimate = 99*[1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1;1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1];end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endx=forecast(1,1)-radar(1,1);y=forecast(2,1)-radar(2,1);z=forecast(3,1)-radar(3,1);dist = norm([x;y;z]);dist_horiz = norm([x;z]);H=[x/dist,y/dist,z/dist,0,0,0;z/dist_horiz^2,0,-x/dist_horiz^2,0,0,0;-x*y/(dist^2*dist_horiz),dist_horiz/dist^2,-y*z/(dist_horiz*dist^2),0,0,0];z_est = measure_func([x;y;z]);if measure==0estimate=forecast;cov_error_estimate = P_forecast;elsekalman_gain = P_forecast*H'/(H*P_forecast*H'+R);estimate = forecast + kalman_gain*(measure - z_est);cov_error_estimate = P_forecast - kalman_gain*H*P_forecast;end
end
end

結果展示：

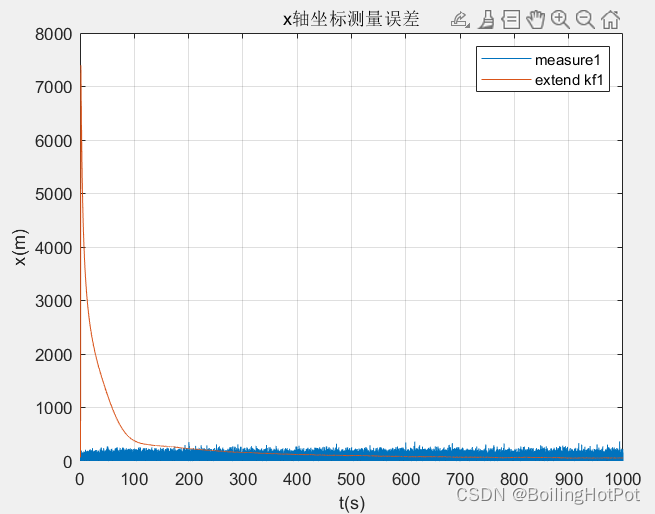
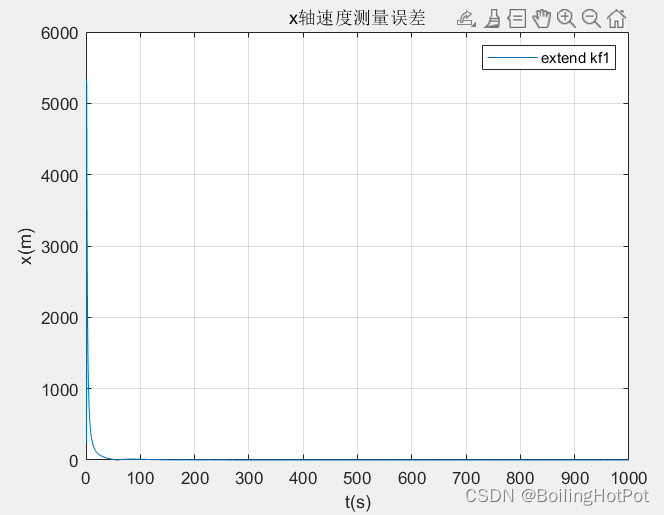
無跡Kalman濾波

無跡變換

設存在一個m維隨機向量和n維隨機向量z，其中z與x為非線性關系

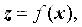
x的均值為，方差為P；x通過非線性映射得到z。無跡變換就是根據x的統計特性，得到一族點集，該點集稱為為σ點；將σ點進行非線性映射可以得的新的點集；通過新的點集得到z的統計特性。一般情況下σ點的數目為2n+1。
無跡變換的具體過程可描述如下：
(1)計算2n+1個點及其權系數


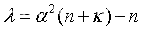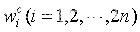其中，決定點的散布程度，通常取正數，通常取為0，β用來代表x的分布情況(正態分布的情況下，最佳值為2)，表示矩陣的平方根的第i列，為用于計算均值的權重，為用于計算方差時的權重。
(2)計算σ點通過非線性函數的傳播結果

從而可得



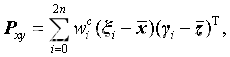
此時，我們得到了無跡變換的結果。

無跡Kalman濾波

針對量測為非線性、狀態轉移為線性的系統模型，無跡Kalman濾波是用無跡變換進行經典卡爾曼濾波中量測方程的映射。
每個遞推無跡Kalman濾波的具體步驟如下：
(1)針對線性目標狀態轉移模型，對于給定的估計和估計誤差協方差，基于經典Kalman濾波求狀態預測以及預報誤差的協方差陣。

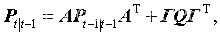
(2)針對非線性傳感器量測模型，用無跡變換求σ點，并通過量測方程的傳播。
計算σ點，即

計算輸出的一步提前預測，即

在獲得新的量測后，進行濾波更新，

代碼及其結果展示

核心代碼：（完整代碼見文末）

function [estimate, cov_error_estimate] = unscented_kf(measure, x_last, P_last,...flag,radar)
%kalman_filter 擴展kalman濾波算法
%   輸入：量測值，上一時刻估計，上一時刻估計誤差協方差,是否預測的標志,
%雷達的狀態信息
%   輸出：當前時刻估計，當前時刻估計誤差協方差
% 當flag為1，則跳過預測步驟
%%
% 狀態轉移矩陣
global A;
% 系統噪聲系數矩陣
global gama;
% 系統噪聲協方差
global Q;
% 量測噪聲協方差
global R;
%%
% 如果全零，即無初始化
if ~any(x_last)if measure==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0時刻，則取量測值對應的狀態為當前時刻估計，9倍的量測誤%差協方差陣為當前時刻估計誤差協方差。%   此處為9的原因是3倍的標準差為百分之95的可能的誤差值，可以認為%包含了最大誤差的情況。% TODO 應該設置為根據實際對象進行變化，這里強制設置為6個狀態，%后續對無跡濾波和此處進行改變，讓其可以根據實際情況進行隨動estimate=[radar(1,1)+measure(1,1)*cos(measure(3,1))*cos(measure(2,1));radar(2,1)+measure(1,1)*sin(measure(3,1));radar(3,1)-measure(1,1)*cos(measure(3,1))*sin(measure(2,1));0;0;0];cov_error_estimate = 1*[1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1;1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1];end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endif measure==0estimate=forecast;cov_error_estimate = P_forecast;else[forecast_point,forecast_weight]=get_point(forecast,P_forecast,size(forecast,1));measure_point = zeros(size(measure,1),size(forecast_point,2));for cou_point = 1:size(forecast_point,2)measure_point(:,cou_point)=measure_func(forecast_point(1:3,cou_point)-radar(1:3,1));endmeasure_expect = sum(forecast_weight(1,:).*measure_point,2);P_z = forecast_weight(2,:).*(measure_point-measure_expect)*...(measure_point-measure_expect)'+R;P_xz = forecast_weight(2,:).*(forecast_point-forecast)*...(measure_point-measure_expect)';kalman_gain = P_xz/P_z;estimate = forecast + kalman_gain*(measure - measure_expect);cov_error_estimate = P_forecast - kalman_gain*P_z*kalman_gain';end
end
end

結果展示：

異步無跡Kalman濾波

在目標狀態估計過程中，量測通常以離散化采樣給出，同時帶有一個探測時間標志。分布式傳感器網絡是對多個量測進行處理。由于傳感器網絡傳輸存在隨機的時間延遲，且各個節點對于量測的預處理時間存在隨機性，很可能出現源于某個目標的較晚的量測到達某一節點后較早的量測才到達該節點，這種情況就稱為非順序量測。在目標狀態估計過程中，傳感器節點通常僅保存航跡的充分統計量。這樣，當接收到一個延遲的量測時，假定該量測的時戳為t，為了實時性，估計結果被更新到tz>t時刻，此時需要使用來自時刻t的量測更新tz時刻的估計。這就是在實際的多傳感器系統中常見的負時間量測更新問題，原因是t-tz為負，而在標準的濾波問題中總假定為非負。通常情況下的濾波算法不適用于這種情況，因此，就需要對適用于異步濾波的算法進行研究。

原理

首先，我們需要對非線性目標運動模型以不同的時間間隔進行重新的離散化定義。對于任意時間間隔的狀態轉移矩陣為；任意時間間隔的噪聲系數矩陣為；任意時間間隔的系統噪聲為

本文僅研究高斯白噪聲隨機過程，則根據隨機積分的性質可知，離散化后的系統噪聲仍為均值為0的高斯白噪聲，其協方差矩陣為

為了便于描述，假定當前時刻為t，而最新的量測時刻為td，且td的量測為t時刻的延遲量測，也就是說

此時，

其中，d為td時刻的簡化標記。可以得到

其中為的逆矩陣，表示后向狀態轉矩矩陣。
我們要解決的問題為：在t時刻，已知目標的狀態估計和估計誤差協方差。同時，我們得到了td時刻的量測。此時，需要用td時刻的量測來更新t時刻狀態估計和估計誤差協方差，即計算

其中。
在最小均方誤差準則下，對于非順序量測問題的最優更新算法為

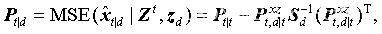
其中，

為了求出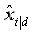，我們需要得到Kd和的值。首先

其中

由傳感器探測模型及最小均方誤差準則得

可知，

其中

的σ點為

根據傳感器探測模型，得

求得計算的σ點為

同理，根據已知的，求得計算的σ點為

計算量測的一步提前預測，即

可知

此時，因為等于0，可得。由最小均方誤差準則可得

帶入式子可求。根據式子可得與

可得的σ點為

根據非線性變換，可得的σ點為

由的σ點可求

可得Kd；將Kd和的帶入可得。接下來，將和帶入即可求出。至此，完成了用td時刻的量測來更新t時刻狀態估計和估計誤差協方差。

代碼及其結果展示

核心代碼：（完整代碼見文末）

function [estimate, cov_error_estimate] = unscented_aysn(measure_aysn,t_asyn,...x_last, P_last,flag,radar,last_est_last,last_P_last,measure)
%kalman_filter 擴展kalman濾波算法
%   輸入：量測值，上一時刻估計，上一時刻估計誤差協方差,是否預測的標志,
%雷達的狀態信息
%   輸出：當前時刻估計，當前時刻估計誤差協方差
% 當flag為1，則跳過預測步驟
%%
global t_step;
% 狀態轉移矩陣
global A;
% 系統噪聲系數矩陣
global gama;
% 系統噪聲協方差
global Q;
% 量測噪聲協方差
global R;
%%
last_est_last = A * last_est_last;
last_P_last = (A*last_P_last *A'+ gama*Q* gama');
% 如果全零，即無初始化
if ~any(x_last)if measure_aysn==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0時刻，則取量測值對應的狀態為當前時刻估計，9倍的量測誤%差協方差陣為當前時刻估計誤差協方差。%   此處為9的原因是3倍的標準差為百分之95的可能的誤差值，可以認為%包含了最大誤差的情況。estimate=[radar(1,1)+measure_aysn(1,1)*cos(measure_aysn(3,1))*cos(measure_aysn(2,1));radar(2,1)+measure_aysn(1,1)*sin(measure_aysn(3,1));radar(3,1)-measure_aysn(1,1)*cos(measure_aysn(3,1))*sin(measure_aysn(2,1));0;0;0];cov_error_estimate = 1*[1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1;1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1];end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endif measure_aysn==0estimate=forecast;cov_error_estimate = P_forecast;elsenum_state = size(forecast,1);Q_td_t =  Q_t1_t2(t_asyn,t_step);[w_td2t_t_1_point,~] = ...get_point(zeros(num_state,1), Q_td_t,3);[last_est_point,last_est_weight] = ...get_point(last_est_last, last_P_last, 3);measure_t_1_point = zeros(size(measure,1),size(last_est_point,2));for cou_point = 1:size(last_est_point,2)measure_t_1_point(:,cou_point)=measure_func(...last_est_point(1:3,cou_point)-radar(1:3,1));endmeasure_expect_t_1 = sum(last_est_weight(1,:).*measure_t_1_point,2);cov_zt_t_1 = last_est_weight(2,:).*(measure_t_1_point-...measure_expect_t_1)*(measure_t_1_point-measure_expect_t_1)'+R;% TODO 應該修正R后的pointcov_w_td2t_zt_t_1= last_est_weight(2,:).*(w_td2t_t_1_point)*...(measure_t_1_point-measure_expect_t_1)';w_td2t = cov_w_td2t_zt_t_1/cov_zt_t_1*(measure-...measure_expect_t_1);cov_w_td2t_t = Q_td_t-cov_w_td2t_zt_t_1/cov_zt_t_1*...cov_w_td2t_zt_t_1';[forecast_point,forecast_weight]=get_point(forecast,P_forecast,3);% (3-25)backcast = A_t1_t2(t_step,t_asyn)*(forecast-w_td2t);P_backcast = A_t1_t2(t_step,t_asyn)*P_forecast*...(A_t1_t2(t_step,t_asyn))'-A_t1_t2(t_step,t_asyn)*...(cov_w_td2t_t)*(A_t1_t2(t_step,t_asyn))';[backcast_point,backcast_weight]=get_point(backcast,P_backcast,3);measure_expect_t_point = zeros(size(measure,1),size(backcast_point,2));for cou_point = 1:size(backcast_point,2)measure_expect_t_point(:,cou_point)=measure_func(...backcast_point(1:3,cou_point)-radar(1:3,1));endmeasure_expect_t = sum(backcast_weight(1,:).*measure_expect_t_point,2);% (3-36)P_z = backcast_weight(2,:).*(measure_expect_t_point-...measure_expect_t)*(measure_expect_t_point-measure_expect_t)'+R;% (3-37)         % TODO 應該修正R后的pointP_xz = forecast_weight(2,:).*(forecast_point-forecast)*...(measure_expect_t_point-measure_expect_t)';kalman_gain = P_xz/P_z;estimate = forecast + kalman_gain*(measure_aysn - measure_expect_t);cov_error_estimate = P_forecast - P_xz/P_z*P_xz';end
end
end

結果展示：


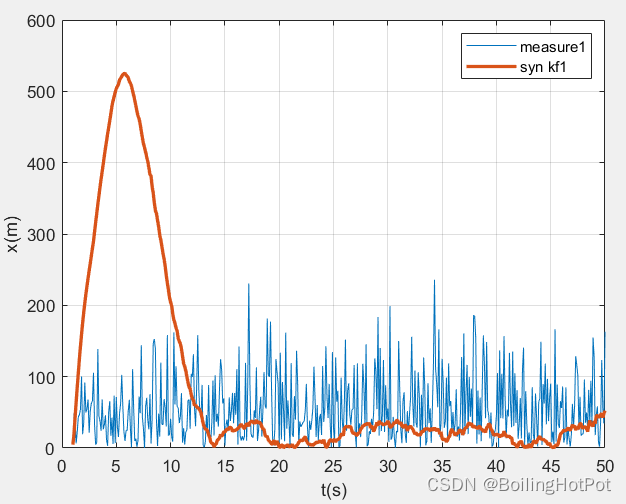
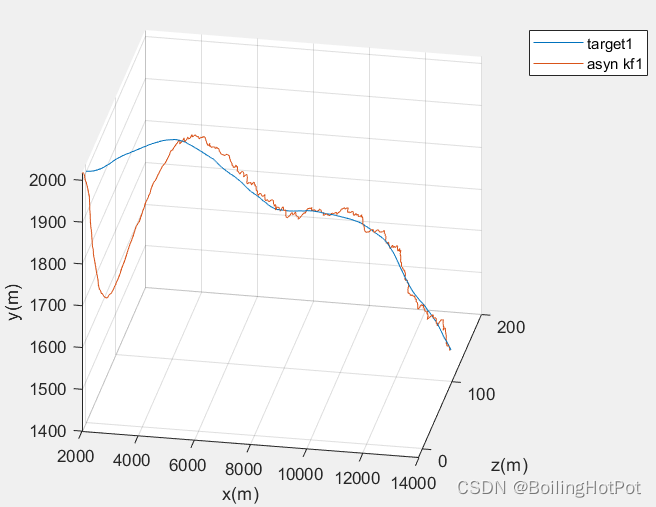
完整代碼分為多個文件，數量較多，無法放在文章中。完整代碼在公眾號（沸騰的火鍋資源號）中自取。