給定一個二叉樹，判斷它是否是高度平衡的二叉樹。

本題中，一棵高度平衡二叉樹定義為：

一個二叉樹每個節點?的左右兩個子樹的高度差的絕對值不超過 1 。

示例 1：

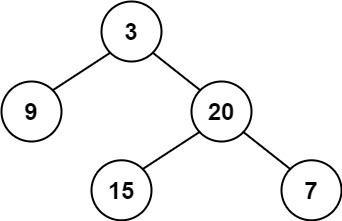
輸入：root = [3,9,20,null,null,15,7]
輸出：true

示例 2：

輸入：root = [1,2,2,3,3,null,null,4,4]
輸出：false

示例 3：

輸入：root = []
輸出：true

提示：

• 樹中的節點數在范圍?[0, 5000]?內
• -104 <= Node.val <= 104

解法：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean isBalanced(TreeNode root) {if (root == null) {return true;}else{//求根節點左子樹和右子樹的差值的絕對值，如果小于1則為平衡二叉樹return Math.abs(Bfs(root.left) - Bfs(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);}}//深度優先遍歷樹public int Bfs(TreeNode root) {if (root == null) {return 0;}//返回最深節點的深度return Math.max(Bfs(root.left), Bfs(root.right)) + 1;}
}

官方解法：

方法二：自底向上的遞歸

方法一由于是自頂向下遞歸，因此對于同一個節點，函數 height 會被重復調用，導致時間復雜度較高。如果使用自底向上的做法，則對于每個節點，函數 height 只會被調用一次。

自底向上遞歸的做法類似于后序遍歷，對于當前遍歷到的節點，先遞歸地判斷其左右子樹是否平衡，再判斷以當前節點為根的子樹是否平衡。如果一棵子樹是平衡的，則返回其高度（高度一定是非負整數），否則返回 ?1。如果存在一棵子樹不平衡，則整個二叉樹一定不平衡。

class Solution {public boolean isBalanced(TreeNode root) {return height(root) >= 0;}public int height(TreeNode root) {if (root == null) {return 0;}int leftHeight = height(root.left);int rightHeight = height(root.right);if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {return -1;} else {return Math.max(leftHeight, rightHeight) + 1;}}
}

復雜度分析

時間復雜度：

O(n)，其中 n 是二叉樹中的節點個數。使用自底向上的遞歸，每個節點的計算高度和判斷是否平衡都只需要處理一次，最壞情況下需要遍歷二叉樹中的所有節點，因此時間復雜度是 O(n)。

空間復雜度：

O(n)，其中 n 是二叉樹中的節點個數。空間復雜度主要取決于遞歸調用的層數，遞歸調用的層數不會超過 n。

---

官方解法部分：

作者：力扣官方題解
鏈接：https://leetcode.cn/problems/balanced-binary-tree/
來源：力扣（LeetCode）
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請注明出處。