粒子群算法核心思想:(鳥 = 粒子)
(1)許多的鳥站在不同的地方;
(2)每一只鳥都有自己尋找食物的初始飛行方向、飛行速度;
(3)這些鳥兒每隔一段時間尋找一次食物,通過搜集所有鳥的信息,來尋找食物最充足的地方;
一、以公式原理的實現過程逐步講解;
1、初始化N個粒子,這些粒子有著隨機的初始位置和隨機的初始速度;
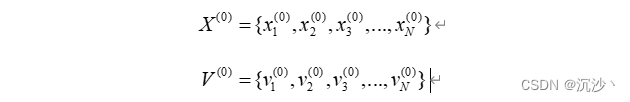
2、計算這些粒子下一步位置,所有的粒子均朝著隨機方向以隨機的速度移動;
![]()
3、尋找所有粒子中的最小值,以及尋找每個粒子在不同時刻的最小值;
先尋找所有粒子中的最小值,對所有的粒子求最小值;
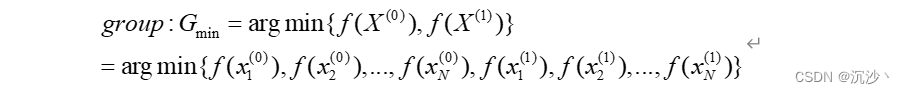
然后選在每個粒子在不同時刻的最小值;每個粒子自身的最小值是能夠決定下一步該粒子移動方向和速度的量;

4、更新粒子搜尋的速度,并且更新粒子搜尋的方向,這里不僅有速度的大小,還有方向的角度,因此是一個矢量;
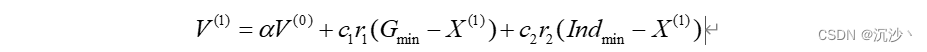
這個里面,隨機優化的核心是其初始位置和速度的隨機性。因此,更新后的速度應一定程度盡可能保持其先前的速度,以保持其隨機性;這個α是慣性權重系數,建議為[0.5,0.8]。
![]()
我們還應該在這次迭代中調整速度以接近組最小值,因為它至少是這一步中最好的一個;這個里面c1是權重系數,r1是隨機權重系數,第一個c1代表全局最小的權重,推薦范圍 0.1-2 ,r1是為了提高隨機性,推薦范圍 0-1;
![]()
另一個同理,c2是代表局部最優的權重,推薦范圍 [0.1~2],r2是隨機權重系數,推薦范圍 0-1;
![]()
5、設計停止條件
重復迭代并在特定位置停止:
(1)達到最大迭代次數k;
(2)變化的目標函數小于預設閾值ε;
? ?(3)我們經常設置速度和位置的限制,以避免不穩定和大的振蕩

二、以代碼進行逐步講解
最后通過代碼進行實現:求取函數最小值

第一步:首先初始化;
1、定義粒子群個數;N = 100; %群體粒子個數
2、定義粒子維數;幾個變量幾維度;D = 2;?
3、定義權重因子大小;c1 =2;c2 =2;
4、定義速度范圍;這個Vmax = 1;?Vmin = -1;
5、定義位置范圍;(變量的范圍)(這里這么寫是因為xy的范圍不一致,就分開給出范圍)
X1max =1;?
X1min =-1;
X2max =3;
X2min =-2;
Xmax = [X1max X2max];
Xmin = [X1min X2min];
第二步:然后定義初始隨機量:
1、定義初始隨機位置;
x1 = ?rand(N,1) * (X1max-X1min)+X1min;?
x2 = ?rand(N,1) * (X2max-X2min)+X2min;
2、定義初始隨機速度;
v = rand(N,D) * (Vmax-Vmin)+Vmin;
第三步:初始化個體最優位置和最優值
p=x; ?
pbest = ones(N,1); %% 創建一個數組,用于存儲每個粒子對應的適應度函數值
for i = 1:N
? ? pbest(i) = func2(x(i,:)); % 求出初始化種群對應的目標函數值
end
第四步:初始化全局最優位置和最優值;
g = ones(1,D);?
gbest = inf;? ?
for i = 1:N? ?
? ? if(pbest(i) < gbest)
? ? ? ? g = p(i,:);
? ? ? ? gbest = pbest(i);
? ? end
end
第五步:粒子群群體尋優;這里就不列了,直接把所有代碼給出來;這里是大頭;
%%%%%%%%%%%%%%粒子群算法求函數極值%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%
function counti()
clear all; %清除所有變量
% close all; %清圖
clc; %清屏
N = 100; %群體粒子個數
D = 2; %粒子維數 變量的個數
T = 1000; %最大迭代次數
c1 =2; %權重因子 c1 [0.1 - 2] 越大,保持原來速度的能力越強
c2 =2; %權重因子 c2 [0.1 - 2]
Wmax = 0.8; %慣性權重最大值
Wmin = 0.4; %慣性權重最小值X1max =1; %位置最大值
X1min =-1; %位置最小值X2max =3; %位置最大值
X2min =-2; %位置最小值Xmax = [X1max X2max];
Xmin = [X1min X2min];Vmax = 1; %速度最大值
Vmin = -1; %速度最小值
%%%%%%%%%%%%初始化種群個體(限定位置和速度)%%%%%%%%%%%%
x1 = rand(N,1) * (X1max-X1min)+X1min;
x2 = rand(N,1) * (X2max-X2min)+X2min;
x = [x1 x2];v = rand(N,D) * (Vmax-Vmin)+Vmin;
%%%%%%%%%%%%%初始化個體最優位置和最優值%%%%%%%%%%%%%
p = x;
pbest = ones(N,1); %% 創建一個數組,用于存儲每個粒子對應的適應度函數值
for i = 1:Npbest(i) = func2(x(i,:)); % 求出初始化種群對應的目標函數值
end
%%%%%%%%%%%%%初始化全局最優位置和最優值%%%%%%%%%%%%
g = ones(1,D); % 創建一個數組和變量用于保存最優變量和目標函數
gbest = inf; %inf 無窮大
for i = 1:N % 這一步當中找到種群最優目標函數值if(pbest(i) < gbest)g = p(i,:);gbest = pbest(i);end
end
gb = ones(1,T); % 建立此項用于保存種群中每一代中的的最優值
%%%%%%%%%按照公式依次迭代直到滿足精度或者迭代次數%%%%%%%%
for i = 1:Tfor j = 1:N%%%%%%%%%更新個體最優位置和最優值%%%%%%%%%%%%%if (func2(x(j,:)) < pbest(j)) % 新的個體是否小于原來的個體,如果小于則保存新的個體p(j,:) = x(j,:);pbest(j) = func2(x(j,:));end%%%%%%%%%%更新全局最優位置和最優值%%%%%%%%%%%%if(pbest(j) < gbest)g = p(j,:);gbest = pbest(j);end%%%%%%%%%%%計算動態慣性權重值%%%%%%%%%%%%%%%w = Wmax-(Wmax-Wmin)*i/T;%%%%%%%%%%%%更新位置和速度值%%%%%%%%%%%%%%%v(j,:) = w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...+c2*rand*(g-x(j,:)); %計算對應的速度公式x(j,:) = x(j,:)+v(j,:); %更新粒子群當中對應的基因%%%%%%%%%%%%%%邊界條件處理%%%%%%%%%%%%%%%% 檢查單個粒子的速度和位置信息是否超過當前最大限制for ii = 1:D % 如果超過的話就在原來的范圍內重新生成個體if (v(j,ii) > Vmax) || (v(j,ii) < Vmin)v(j,ii) = rand * (Vmax-Vmin)+Vmin;end if (x(j,ii) > Xmax(ii)) || (x(j,ii) < Xmin(ii))x(j,ii) = rand * (Xmax(ii)-Xmin(ii))+Xmin(ii);endendend%%%%%%%%%%%%%%記錄歷代全局最優值%%%%%%%%%%%%%%gb(i) = gbest;
end
g; %最優個體
gb(end); %最優值
figure(1)
plot(gb)
hold on
grid on
xlabel('迭代次數');
ylabel('適應度值');
title('適應度進化曲線')
hold on
end
%%%%%%%%%%%%%%%%%%適應度函數%%%%%%%%%%%%%%%%%function value = func2(x)
value = (3*cos(x(1)*x(2))+x(1)+x(2)^2);end %這里是適應度函數,也可以在同一文件夾下獨立建立函數,也可以直接寫在后面。最終仿真結果:
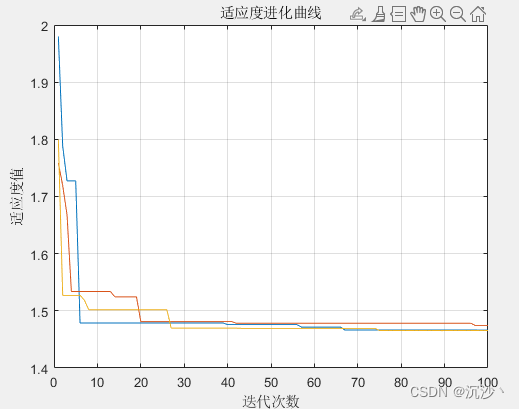
)
)









)


深度學習環境配置筆記)




