Course3-Week1-無監督學習

• 筆記主要參考B站視頻“(強推|雙字)2022吳恩達機器學習Deeplearning.ai課程”。
• 該課程在Course上的頁面：Machine Learning 專項課程
• 課程資料：“UP主提供資料(Github)”、或者“我的下載(百度網盤)”。
• 本篇筆記對應課程 Course3-Week1（下圖中深紫色）。

---

1. 歡迎

1.1 Course3簡介

前面的Course1、Course2一直在討論“有監督的機器學習”，Course3就來介紹不一樣的內容：

• Week1-無監督機器學習(unsupervised learning)：主要學習“聚類(clustering)”及“異常檢測(anomaly detection)”，這兩種技術都廣泛應用于商業軟件中。
• Week2-推薦機制(recommender systems)：“推薦系統”是機器學習最重要的商業應用之一，影響的產值達到數十億美元，但在學術界卻并沒有取得相應的關注。常見于購物網站、流媒體視頻等“為你推薦/猜你喜歡”的功能，學完后將理解廣告的推薦策略。
• Week3-強化學習(reinforcement learning)：“強化學習”是一項新的技術，和前面提到的技術相比，商業應用沒有那么廣泛。但這是一項令人興奮的技術，它向人們展示了學習算法可以做的事情，比如打游戲、控制機器人等。課程最后將使用“強化學習”模擬一個月球著陸器。

1.2 數學符號約定

下面是本周會用到的數學符號，下面用到了再查就行。

數學符號約定：

• 樣本數量為$m$、特征的數量為$n$、質心的數量為 $K$。
• ${\vec{x}}^{(i)}$：是 $n$維向量，用于表示第 $i$ 個樣本的位置。
• ${\vec{\mu }}_k$：是 $n$維向量，用于表示第 $k$ 個質心的位置。
• $c^{(i)}$：一個值，取值范圍1~$K$，表示第 $i$ 個樣本 ${\vec{x}}^{(i)}$ 所對應的質心索引，該質心到 ${\vec{x}}^{(i)}$ 的歐式距離最短。
• ${\vec{\mu }}_{c^{(i)}}$：表示第 $i$ 個樣本 ${\vec{x}}^{(i)}$ 所對應的質心 $c^{(i)}$ 的位置。等價于 ${\vec{\mu }}_k$，只不過為了強調是 ${\vec{x}}^{(i)}$ 所對應的質心。
• $\Vert x^{(i)}?{\mu }_k\Vert$：二階范數，表示第 $i$ 個樣本 ${\vec{x}}^{(i)}$ 和第 $k$ 個質心之間的歐式距離。但實際在代碼中為減少計算量，通常使用該距離的平方，寫成范數是為了數學形式的簡便。
• X = { x ? ( 1 ) ; x ? ( 2 ) ; . . . ; x ? ( n ) } X = \{ \vec{x}^{(1)};\vec{x}^{(2)};...;\vec{x}^{(n)} \} X={x (1);x (2);...;x (n)}：是 $m\times n$ 二維矩陣，每一行表示一個樣本的位置。
• M = { μ ? 1 ; μ ? 2 ; . . . ; μ ? K } \Mu = \{ \vec{\mu}_1;\vec{\mu}_2;...;\vec{\mu}_K \} M={μ ?1?;μ ?2?;...;μ ?K?}：是 $K\times n$ 二維矩陣，每一行表示一個質心的位置。
• c ? = { c ( 1 ) , c ( 2 ) , . . . , c ( m ) } \vec{c} = \{ c^{(1)},c^{(2)},...,c^{(m)} \} c ={c(1),c(2),...,c(m)}：是 $m$維向量，每個數都表示一個樣本對應的質心索引。

注：上述中，“位置”向量中的每個參數都表示一個特征。
注：視頻中老師沒有標注向量符號，為了嚴謹且方便敘述，我標注上了。

2. K-means算法

??“聚類(clustering)”算法會自動將相似的數據點歸為一類。和“有監督學習”不同，“聚類”這樣的“無監督學習”算法的數據集沒有標簽。比如在Course1-Week1-2.2節中給出的一系列“無監督學習”示例：新聞分類、基因分類、客戶分群、天文數據分析等。并且，“聚類”算法除了被用于有很明顯分組的數據集，也可以對沒有明顯分組的數據集進行分類，比如設計T恤時的S、M、L尺碼。

2.1 K-means算法的步驟

??“K-means算法”是最常見的聚類算法，下面簡單介紹一下“K-means算法”的原理。如下圖所示，假設現在數據集中有30個未標記的訓練樣本，要求將數據分成兩類。于是，我們可以先隨機初始化兩個“質心(centroid)”，然后不斷的重復下面的步驟，直到質心的位置不再變化，也就是“收斂”：

1. 為所有樣本分配“質心”。也就是將當前樣本，分配給距離最近的“質心”。
2. 移動每一個“質心”。使用當前質心的所有樣本計算出新的質心位置。

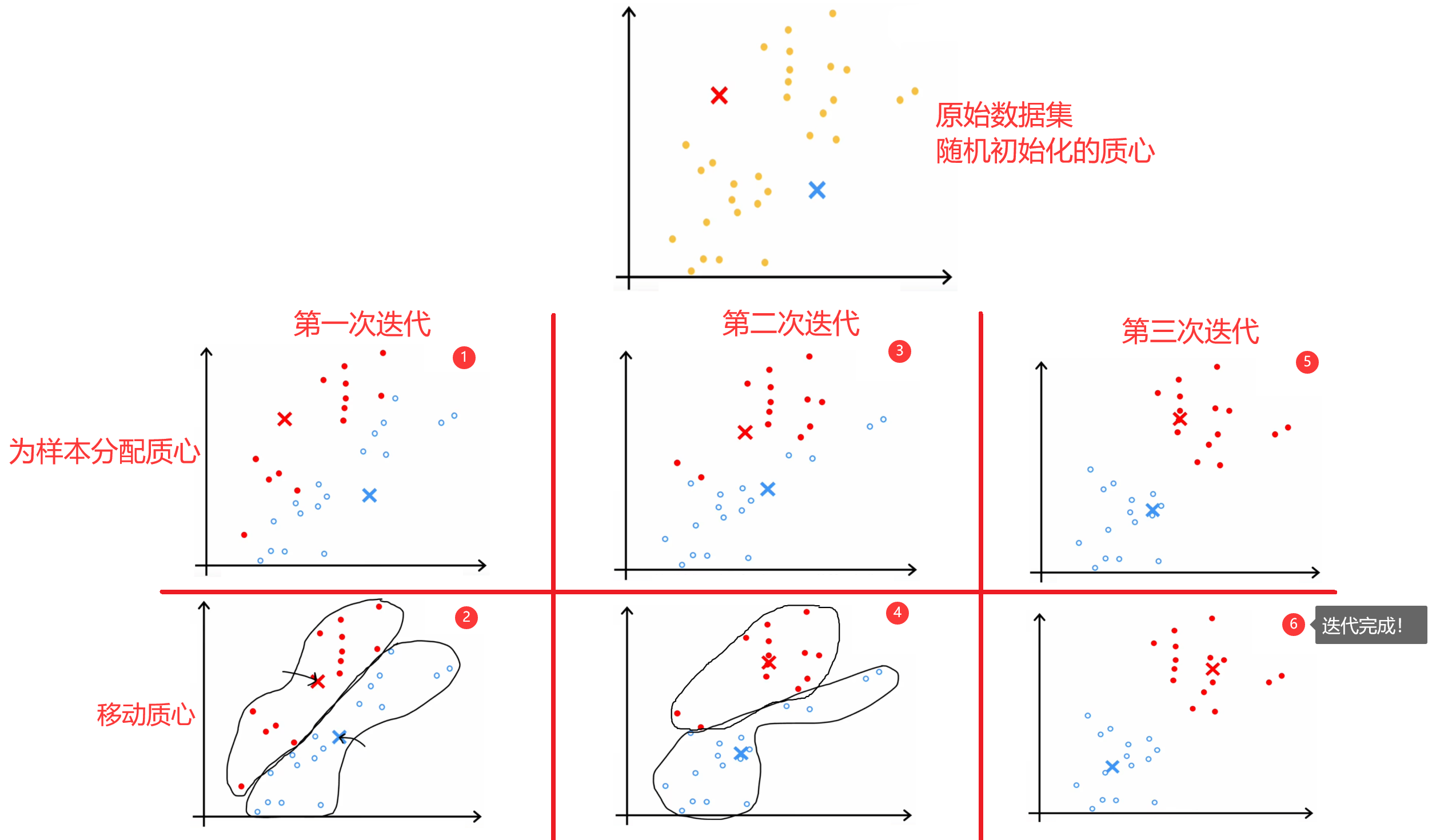
但“隨機初始化”有一定的風險，因為不同的初始化會導致不同的聚類結果，所以很多迭代過程都會陷入到“局部最優解”中，如下圖所示。所以解決方法就是將上述過程運行50~1000次，每次運行結束時都計算本次的代價函數，最終就可以找出代價最低的聚類結果。下面給出完整的“K-means算法”步驟：

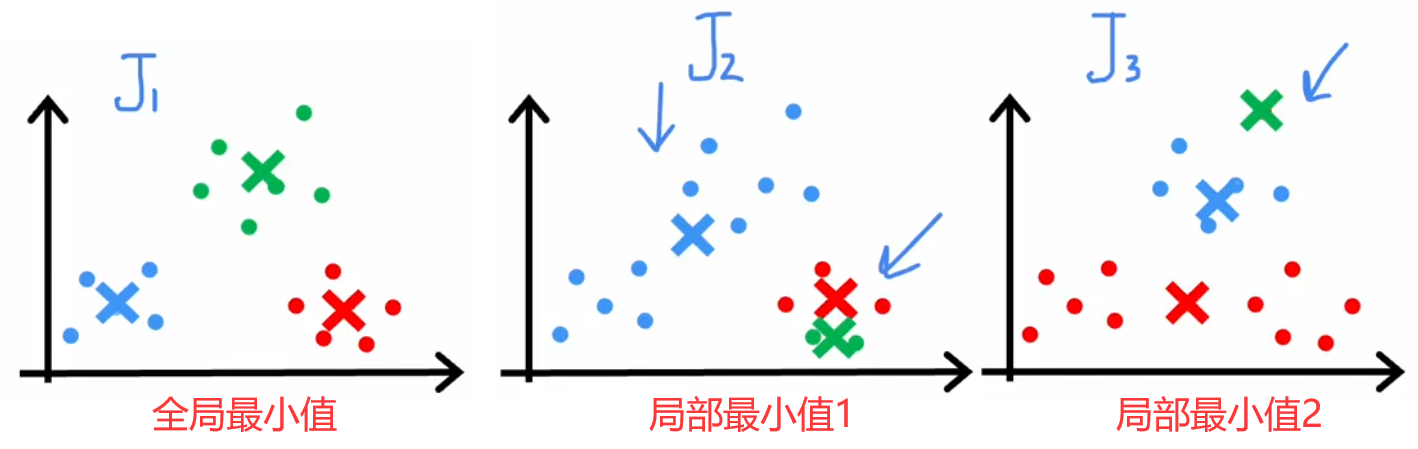
完整的K-means算法：

1. 設定重復次數(如100次)：{
   ??1. 隨機選擇 $K$ 個不同的樣本作為 $K$ 個質心的初始位置：${\vec{\mu }}_1,{\vec{\mu }}_2,...,{\vec{\mu }}_K$
   ??2. 然后不斷重復：{
   ????1. 為樣本分配質心。針對 $m$ 個樣本，重復 $m$ 次，利用 $X$、$\mathrm{M}$ 計算出距離當前樣本最近的質心索引。最后得到 $\vec{c}$。
   ????2. 移動質心。針對 $K$ 個質心，重復 $K$ 次，利用 $\vec{c}$ 計算出每個質心的新位置，并移動。質心的新位置等于該質心對應的所有樣本位置的平均值。
   ??}直到質心不再移動或移動步長很小(收斂)；
   ??3. 計算并保存當前結果的代價。
   }
2. 找出代價最小的聚類結果。

注1：特征數量為$n$、樣本數量為$m$、質心數量為$K$。
注2：運行次數超過1000后，計算成本很高，但帶來的收益很小，所以一般運行50~1000次即可。
注3：下一小節介紹“代價函數”的數學形式。

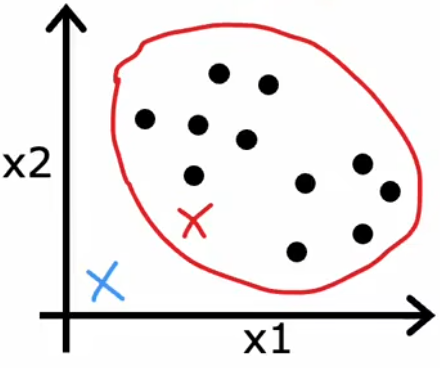
最后注意，若某次迭代結束后，某質心沒有被分配到樣本，如下圖所示，那么：

1. 去掉一個質心，也就是令 $K=K?1$【常用】。
2. 重新初始化質心位置，重新迭代。

2.2 代價函數

??上述介紹的整個“K-means算法”的過程，和“梯度下降法”相似，實質上也是在尋找特定代價函數的最小值。這個代價函數就是樣本和其質點的距離的平方和的平均，在某些文獻中也被稱為“失真函數(distoration function)”：
$$\begin{array}{rl}\text{Cost?Function/}& \\ \text{Distoration?Function}& \end{array}:J(\vec{c},\mathrm{M})=\frac{1}{m}\sum _{i=1}^m\Vert x^{(i)}?{\mu }_{c^{(i)}}{\Vert }^2$$

所以，K-means算法實際上就是想讓上述的距離的平均平方和最小。每次迭代中，代價函數都應該下降或不變，若代價不變或者下降的非常小則表明算法收斂，若代價上升則意味著代碼有bug。

2.3 選擇聚類數量

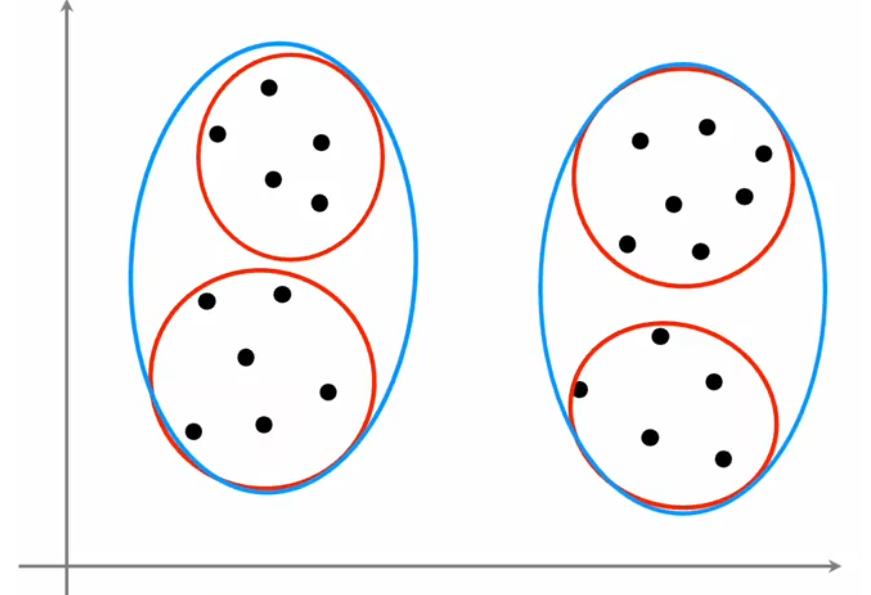
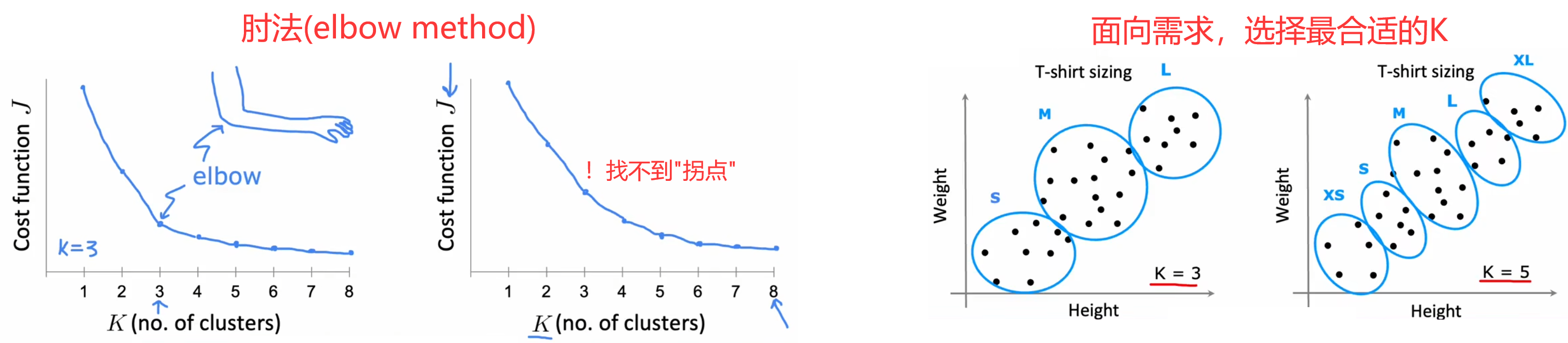
??由于“K-means算法”屬于“無監督學習”，所以聚類數量 $K$ 是很主觀的指標，沒有絕對正確的聚類數量。比如上圖中，聚類數量是2、3、4，都非常合理。另外，聚類數量越多，代價函數的全局最小值越小，極端情況下令 $K=m$，此時每個樣本都是一個類，顯然代價為0最小。但通常來說，我們使用下面兩種方法選擇聚類數量 $K$：

1. “肘法(elbow method)”【不推薦】：畫出代價函數的全局最小值 $J_{min}$ 隨著 $K$ 變化的曲線，找出曲線“拐點(肘部)”所對應的 $K$ 作為最佳的聚類數量。但缺點是在大多數情況下，曲線都很平滑，找不到“拐點”。
2. 面向需求【推薦】：通常當前的算法都會有后續的應用，所以可以根據應用需求選取相應的聚類數量。比如前面的“選擇T恤尺碼”問題，可以看設計需要選擇3種尺碼還是5種尺碼，當然更多的尺碼也意味著更多的成本，所以可以都運行一下，綜合考慮最后結果再選擇聚類數量。

本節 Quiz：

1. Which of these best describes unsupervised learning?
   × A form of machine learning that finds patterns using labeled data (x,y).
   × A form of machine learning that finds patterns in data using only labels (y) but without any inputs (x).
   √ A form of machine learning that finds patterns using unlabeled data (x).
   × A form of machine learning that finds patterns without using a cost function.

2. Which of these statements are true about K-means? Check all that apply.
   √ If you are running K-means with $K=3$ clusters, then each $c^{(i)}$ should be 1,2,or3.
   √ If each example x is a vector of 5 numbers, then each cluster centroid ${\mu }_k$ is also going to be a vector of 5 numbers.
   × The number of cluster centroids ${\mu }_k$ is equal to the number of examples.
   √ The number of cluster assignment variables $c^{(i)}$ is equal to the number of training examples.

3. You run K-means 100 times with different initializations. How should you pick from the 100 resulting solutions?
   × Pick the last one (i.e., the 100th random initialization) because K-means always improves over time.
   × Average all 100 solutions together.
   × Pick randomly - that was the point of random initialization.
   √ Pick the one with the lowest cost $J$.

4. You run K-means and compute the value of the cost function $J(c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_k)$ after each iteration. Which of these statements should be true?
   × Because K-means tries to maximize cost, the cost is always greater than or equal to the cost in the previous iteration.
   × There is no cost function for the K-means algorithm.
   × The cost can be greater or smaller than the cost in the previous iteration, but it decreases in the long run.
   √ The cost will either decrease or stay the same after each iteration.

5. In K-means, the elbow method is a method to
   × Choose the best number of samples in the dataset
   × Choose the maximum number of examples for each cluster
   × Choose the best random initialization
   √ Choose the number of clusters K

3. 異常檢測

下面來學習第二種商業應用廣泛的“無監督學習”算法——“異常檢測(anomaly detection)”。

3.1 異常檢測的直觀理解

【問題1】“飛機引擎檢測”：根據輸入特征，檢測新制造的引擎是否有問題。

• 輸入特征：“發動機溫度”、“振動強度”。實際顯然會有更多的特征，這里做出了簡化。
• 輸出：是否異常。
• 訓練集：$m$ 個正常引擎的特征。

【問題2】“金融欺詐監測”：持續監測用戶特征，判斷是否有可能的欺詐行為。

• 輸入特征：正常用戶的登錄頻率、單次訪問網頁數量、單次交易數量、單次發帖數量、打字速度等。
• 輸出：查看某個新用戶是否具有欺詐行為。

【問題3】“服務器監測”：監測數據中心的服務器是否正常運行。

• 輸入特征：內存使用量、磁盤讀寫次數、CPU負載、網絡流量等。
• 輸出：判斷服務器是否出現異常行為，比如被黑客攻擊等。

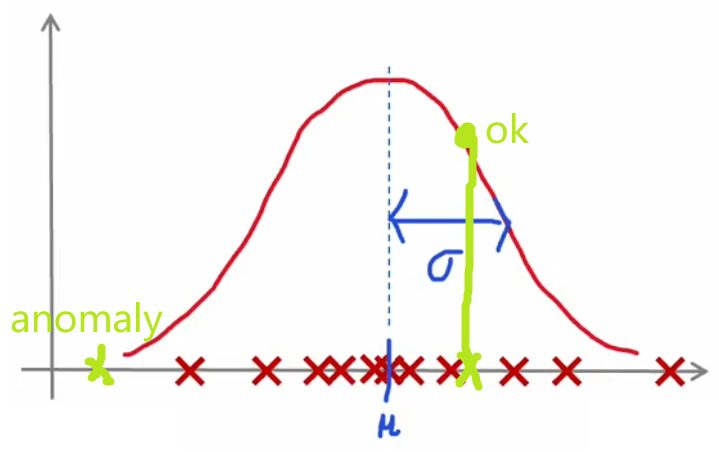
??“異常檢測”通常使用“(概率)密度估計(density estimation)”的方法。也就是，“異常檢測”算法首先使用未標記的正常事件數據集進行訓練(下圖紅叉)，學習正常樣本的概率分布，然后計算新樣本 $x_{test}$ 出現的概率，若其出現的概率小于設定好的閾值 $p(x_{test})<\epsilon$，顯然就可以認為這是一個異常事件：

3.2 高斯分布

??由于幾乎所有從自然界采集的數據都服從高斯分布，所以我們使用高斯分布進行概率密度估計，本小節就來介紹“高斯分布(Gaussian distribution)”。下面是高斯分布的性質及表達式：

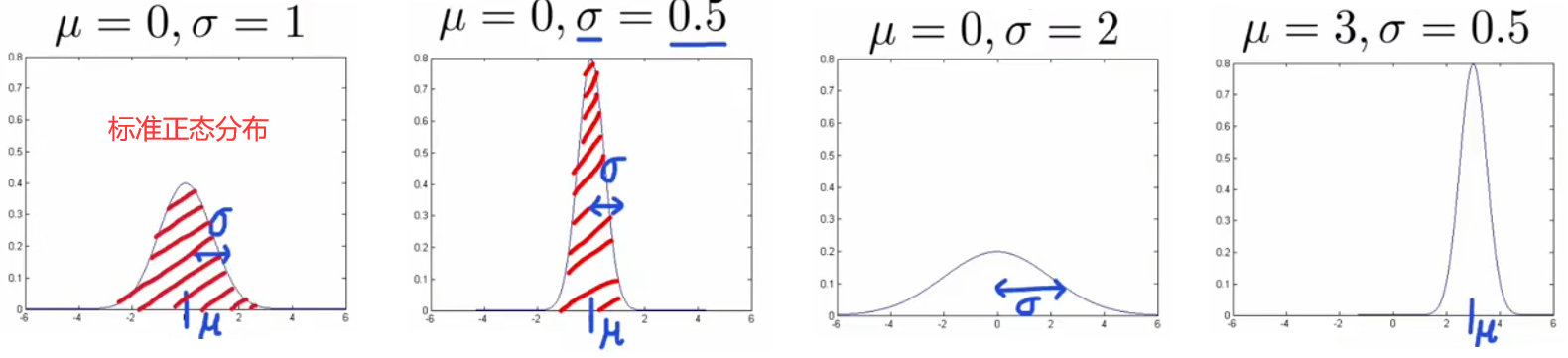
• 均值 $\mu$ 只是沿坐標軸平移曲線，不改變曲線形狀。
• 方差 ${\sigma }^2$ 越大，曲線越扁平；方差 ${\sigma }^2$ 越小，曲線越集中。
• 概率和為1，所以 ${\int }_{?\infty }^{+\infty }p(x)dx=1$。
• $3\sigma$原則：$x$ 出現在 $(\mu ?3\sigma ,\mu +3\sigma )$ 以外的概率小于 $0.3\%$，便認為是異常事件。根據精度要求，該標準可以在 $3\sigma ～6\sigma$ 間浮動。

注：“高斯分布”別稱“正態分布(Normal distribution)”、“鐘形分布(Bell-shaped distribution)”，以下皆稱“高斯分布”。

$$\text{Gussion?Distribution:}p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{?(x?\mu {)}^2}{2{\sigma }^2}}$$

通過上述可以看到，高斯分布由均值 $\mu$ 和 方差 ${\sigma }^2$ 完全確定。于是針對某單個特征，我們就可以計算其均值和方差，來對當前特征進行高斯估計(假設樣本$x^{(i)}$只有一個特征)：
$$\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)},{\sigma }^2=\frac{1}{m}\sum _{i=1}^m(x^{(i)}?\mu {)}^2.$$

3.3 異常檢測算法

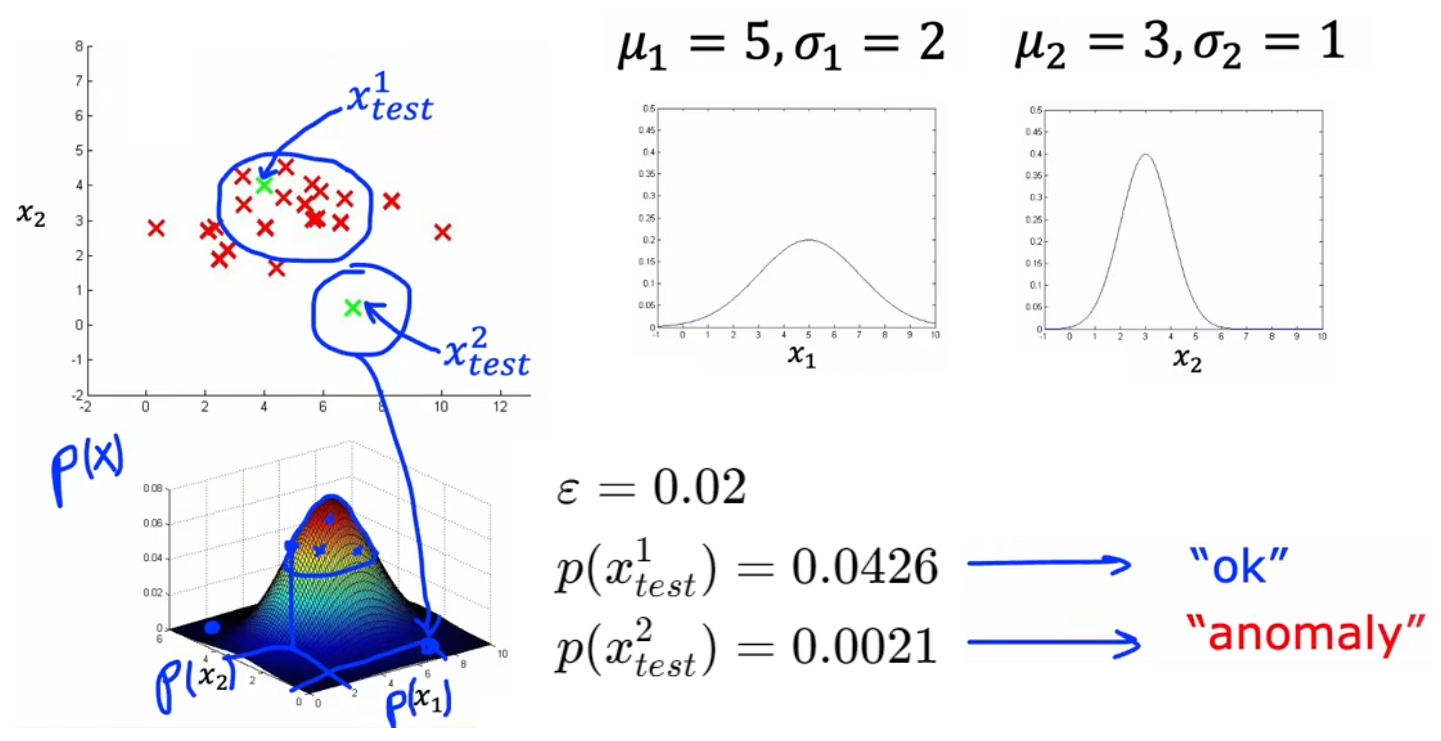
??于是，根據上一節對單個特征進行高斯估計的公式，可以很容易的推廣到具有多特征的樣本，于是就可以寫出下面“異常檢測”算法的完整步驟。以3.1節的“飛機引擎檢測”問題舉例，首先使用正常樣本分別對特征 $x_1$、$x_2$ 進行概率統計，獲得整體的概率統計后，就可以直接計算 $p(x_{test})$ 來判斷其是否為異常事件：

“異常檢測”算法的完整步驟：

1. 定義訓練集，注意全部為正常樣本。假設樣本總數為 $m$、特征總數為 $n$。
2. 對每個特征分別進行統計分析，然后將其相乘得到某樣本的綜合概率分布。這里假設所有特征都服從高斯分布，并且相互獨立。就算不獨立，算法表現依舊良好：
   $$\begin{gathered} {\mu }_j=\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)},{\sigma }_j^2=\frac{1}{m}\sum _{i=1}^m(x_j^{(i)}?{\mu }_j{)}^2,j=1,2,...,n. \\ p(\vec{x})=p(x_1;{\mu }_1,{\sigma }_1^2)?p(x_2;{\mu }_2,{\sigma }_2^2)?...?p(x_n;{\mu }_n,{\sigma }_n^2)=\prod _{j=1}^{n}p(x_j;{\mu }_j,{\sigma }_j^2) \end{gathered}$$
3. 對于新的輸入 ${\vec{x}}_{new}$，代入 $p(\vec{x})$ 計算其概率。若 $p({\vec{x}}_{new})<\epsilon$ 則認為是異常事件。

下一小節來介紹如何選取合適的判斷閾值 $\epsilon$。

3.4 選取判斷閾值 $\epsilon$

??顯然在開發系統時，如果有一個具體的評估系統性能的指標，就很容易幫助我們改進系統，這就是“實數評估(real-number evaluation)”。由于 $\epsilon$ 也是“異常檢測”的模型參數，于是這啟示我們借鑒“有監督學習”中的“驗證集”這一概念，來選擇最合適的模型參數 $\epsilon$。我們可以將“是否異常”看成是一種標簽，來進行如下拆分，注意“訓練集”是全部都為正常樣本的無標簽數據：

1. 【異常樣本足夠】三拆分：訓練集、驗證集、測試集。

• 原始訓練集：10000正常樣本 + 20異常樣本。
• 訓練集：6000正常樣本。用于擬合正常樣本的概率分布。
• 驗證集：2000正常樣本+10異常樣本。用于挑選最合適的 $\epsilon$ 或者改進特征。
• 測試集：2000正常樣本+10異常樣本。用于最后評估系統性能。

2. 【異常樣本極少】二拆分：訓練集、驗證集。

• 原始訓練集：10000正常樣本 + 2異常樣本。
• 訓練集：6000正常樣本。用于擬合正常樣本的概率分布。
• 驗證集：4000正常樣本+2異常樣本。用于挑選最合適的 $\epsilon$ 或者改進特征。

注1：上述“二拆分”沒有“測試集”評估系統性能，可能會有“過擬合”的風險。
注2：由于訓練集沒有標簽，所以上述依舊是“無監督學習”。

進行上述拆分后，注意到上述“驗證集”、“訓練集”都屬于Course2-Week3-第4節提到的“傾斜數據集”，于是就可以使用“準確率/召回率”、“F1 score”來評判系統在“驗證集”、“測試集”上的性能。一個可行的代碼思路是：

# 1. 訓練結束后，計算驗證集中所有樣本對應的概率p_cv(0~1)。
# 2. 計算每個步長所對應的“F1 score”：
step = (max(p_cv) - min(p_cv)) / 1000
for epsilon in numpy.arange(min(p_cv), max(p_cv), step):# 計算當前 epsilon 下的“F1 score”
# 3. 找出最大的“F1 score”所對應的epsilon即可。

3.5 選擇恰當的特征

??在“有監督學習”中，即使選取的特征沒那么恰當也沒關系，因為算法可以從數據集的標簽中學到如何重新縮放特征。但“無監督學習”的訓練集沒有標簽，這就意味著 相比于“有監督學習”，選擇恰當的特征對于“無監督學習”來說更重要。和前面類似，改進特征的方法主要有“特征變換”、“誤差分析”：

特征變換：尋找更合適的概率分布

若原始特征不是高斯分布，那顯然會引入很大的誤差，于是：

1. 進行特征變換(如下圖)：通過數學變換將其變換成高斯分布。常見的改進方法有取對數 $\log (x+c)$，$c$為常數；冪次 $x^n$，$n$為任意實數。
2. 使用其他分布進行擬合。如下圖左側就是“對數正態分布”，其他的還有“瑞利分布”、“指數分布”等。

注：上述兩種方法原理相通，只不過方法二需要了解常見的統計分布。

誤差分析

如果在“驗證集”上表現不佳，那么也可以進行“誤差分析”，分析出現錯誤的原因，對癥下藥進行改進：

1. 引入新特征：比如在“金融欺詐監測”中，檢查某個被遺漏的異常樣本，發現指標“交易次數$x_1$”略高但在正常范圍內，但是打字速度非常快，那么就可以添加新的特征“打字速度$x_2$”。
2. 組合舊特征：比如在“服務器監測”中，檢查某個被遺漏的異常樣本，所有指標都在合理范圍內，只是“CPU負載$x_3$”略高且“網絡流量$x_4$”略低，那么就可以組合這兩個特征“CPU負載/網絡流量$x_5$”。

3.6 異常檢測與有監督學習對比

??既然3.4節引入了“驗證集”，將異常樣本標記為1、正常樣本標記為0，那為什么不使用前面的“有監督學習”完成檢測異常樣本的任務呢？這是因為兩者的問題重心不同。總結一句話，“異常檢測”嘗試檢測出“新異常”；“有監督學習”只檢測“舊異常”。下面給出兩者的對比：

異常檢測-無監督學習：

• 異常樣本極少。
• 異常的種類很多，異常樣本無法覆蓋到所有的異常；并且時常出現“新異常”。

• 如“金融欺詐監測”，每隔幾個月都會出現全新的欺詐策略。
• 如“飛機引擎檢測”，希望能檢測到全新的缺陷。
• 如“服務器監測”，因為有人維護，所以黑客每次的入侵方式都不一樣。許多系統安全相關的軟件都使用“異常檢測”。

有監督學習：

• 異常樣本很多，甚至和正常樣本一樣多。
• 異常樣本覆蓋全面，以后出現的異常幾乎都是之前出現過的。

• 如“垃圾郵件分類器”，內容無外乎保險、毒品、商品推銷等。
• 如“產品缺陷檢測”，流水線產品的缺陷幾乎已經都是固定種類的，比如擦痕檢測。
• 如“天氣預報”，因為天氣的種類是固定的：晴天、雨天等。
• 如“疾病檢測”，看看病人是否有特定類型的疾病。

本節 Quiz：

1. You are building a system to detect if computers in a data center are malfunctioning. You have 10,000 data points of computers functioning well, and no data from computers malfunctioning. What type of algorithm should you use?
   √ Anomaly detection
   × Supervised learning

2. You are building a system to detect if computers in a data center are malfunctioning. You have 10,000 data points of computers functioning well, and 10,000 data points of computers malfunctioning. What type of algorithm should you use?
   × Anomaly detection
   √ Supervised learning

3. Say you have 5,000 examples of normal airplane engines, and 15 examples of anomalous engines. How would you use the 15 examples of anomalous engines to evaluate your anomaly detection algorithm?
   × Because you have data of both normal and anomalous engines, don’t use anomaly detection. Use supervised learning instead.
   × You cannot evaluate an anomaly detection algorithm because it is an unsupervised learning algorithm.
   √ Put the data of anomalous engines (together with some normal engines) in the cross-validation and/or test sets to measure if the learned model can correctly detect anomalous engines.
   × Use it during training by ftting one Gaussian model to the normal engines, and a different Gaussian model to the anomalous engines.

4. Anomaly detection flags a new input $x$ as an anomaly if $p(x)<\epsilon$. If we reduce the value of $\epsilon$, what happens?
   × The algorithm is more likely to classify new examples as an anomaly.
   √ The algorithm is less likely to classify new examples as an anomaly.
   × The algorithm is more likely to classify some examples as an anomaly, and less likely to classify some examples as an anomaly. It depends on the example $x$.
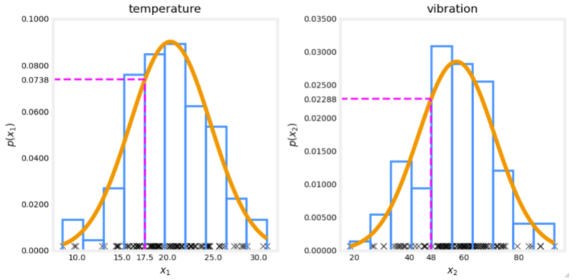
   × The algorithm will automatically choose parameters $\mu$ and $\sigma$ to decrease $p(x)$ and compensate.

5. You are monitoring the temperature and vibration intensity on newly manufactured aircraft engines. You have measured 100 engines and fit the Gaussian model described in the video lectures to the data. The 100 examples and the resulting distributions are shown in the figure below.
   The measurements on the latest engine you are testing have a temperature of 17.5 and a vibration intensity of 48. These are shown in magenta on the figure below. What is the probability of an engine having these two measurements?
   Answer: 0.0738*0.02288 = 0.00169