王道數據結構課后代碼題 p149 第3—— 7（c語言代碼實現）

目錄

3.編寫后序遍歷二叉樹的非遞歸算法

?4.試給出二叉樹的自下而上、自右到左的層次遍歷算法 （有圖解代碼詳解）c語言代碼實現

5.假設二叉樹采用二叉鏈表存儲結構，設計一個非遞歸算法求二叉樹的高度。

?編輯

?6.設一棵二叉樹中各結點的值互不相同，其先序遍歷序列和中序遍歷序列分別存于兩個一維數組A[l...n]和 B[l...n]中，試編寫算法建立該二叉樹的二叉鏈表。

?7.二叉樹按二叉鏈表形式存儲，寫一個判別給定二叉樹是否是完全二叉樹的算法

3.編寫后序遍歷二叉樹的非遞歸算法

?本題代碼如下

void postorder(tree* t)
{struct treenode* stack[100];//初始化結構體數組int top = -1;//讓棧頂指向-1treenode* p = *t;while (p || top != -1)//p不為空，并且棧不為空{if (p){top++;//p不為空，將p壓入棧中stack[top] = p;p = p->lchild;//一直向左下遍歷}else{p = stack[top];//p等于棧頂元素if (p->rchild && p->rchild->tag == 0)//右孩子不為空且未被訪問過p = p->rchild;else//否則彈出結點并訪問{p = stack[top];top--;printf("%c", p->data);p->tag = 1;//標記p被訪問過p = NULL;}}}
}

完整測試代碼

#include<stdio.h>
#include<stdlib.h>
typedef struct treenode
{char data;struct treenode* lchild, * rchild;int tag;
}treenode,*tree;
void buildtree(tree *t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->tag = 0;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
void postorder(tree* t)
{struct treenode* stack[100];//初始化結構體數組int top = -1;//讓棧頂指向-1treenode* p = *t;while (p || top != -1)//p不為空，并且棧不為空{if (p){top++;//p不為空，將p壓入棧中stack[top] = p;p = p->lchild;//一直向左下遍歷}else{p = stack[top];//p等于棧頂元素if (p->rchild && p->rchild->tag == 0)//右孩子不為空且未被訪問過p = p->rchild;else//否則彈出結點并訪問{p = stack[top];top--;printf("%c", p->data);p->tag = 1;//標記p被訪問過p = NULL;}}}
}
int main()
{tree t;buildtree(&t);postorder(&t);return 0;
}

用ABD##E##CF##G##

/*?? ??? ?A
?? ?B?? ??? ?C
D?? ? ?E ? F ? ? G?? ?
*/

?4.試給出二叉樹的自下而上、自右到左的層次遍歷算法 （有圖解代碼詳解）c語言代碼實現

?本題我們采用讓結點出隊時將結點入棧，同時訪問該結點，是否有左右孩子，如果有的話，就讓左右孩子進隊。最后所有結點都入棧了，再從棧頂開始依次訪問就可以得到結果

看下面的圖解

A先入隊，然后出隊，就壓入棧中

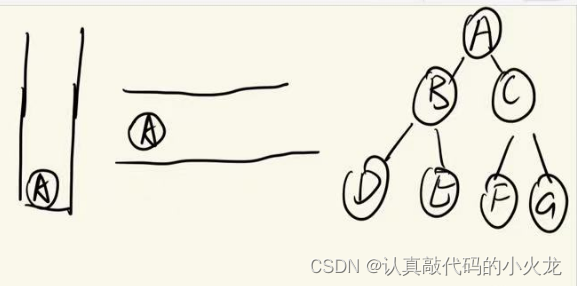
訪問A結點，有左右孩子，左右孩子入隊

B結點出隊并入棧，并訪問B結點，B結點有左右孩子，左右孩子進隊

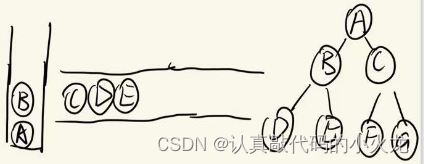
C結點出隊并入棧，同時訪問C結點，C結點有左右孩子，左右孩子進隊

D結點出隊并入棧，同時訪問D結點，D結點沒有左右孩子

EFG依次出隊進棧（與D的步驟相同）

最后我們看一下棧中的元素

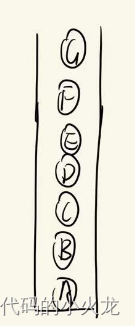
我們讓棧中元素依次出棧就能得到我們想要的結果

下面我們來看一下代碼該如何實現：

void level(tree* t)
{treenode* q[10];treenode* s[10];int top = -1;int f = -1;int r = -1;treenode* p;q[++r] = *t;//根結點進隊while (f < r){p = q[++f];//結點出隊s[++top] = p;//結點進棧if (p->lchild)//出隊結點是否有左孩子q[++r] = p->lchild;//有左孩子，左孩子進棧if (p->rchild)//出隊結點是否有右孩子q[++r] = p->rchild;//有右孩子，右孩子進棧}while (top != -1)//依次輸出棧中元素{printf("%c ", s[top--]->data);}
}

完整測試代碼如下

#include<stdio.h>
#include<stdlib.h>
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode,*tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
void level(tree* t)
{treenode* q[10];treenode* s[10];int top = -1;int f = -1;int r = -1;treenode* p;q[++r] = *t;while (f < r){p = q[++f];s[++top] = p;if (p->lchild)q[++r] = p->lchild;if (p->rchild)q[++r] = p->rchild;}while (top != -1){printf("%c ", s[top--]->data);}
}
int main()
{tree t;buildtree(&t);level(&t);return 0;
}

用ABD##E##CF##G##測試

5.假設二叉樹采用二叉鏈表存儲結構，設計一個非遞歸算法求二叉樹的高度。

?采用層次遍歷的算法，設置變量 ans記錄當前結點所在的層數，設置變量 l?指向當前層的最右結點，每次層次遍歷出隊時與 l指針比較，若兩者相等，則層數加 1，并讓 l指向下一層的最右結點，直到遍歷完成。ans的值即為二又樹的高度。

本題代碼如下

int deep(tree* t)//求樹的深度
{if ((*t) == NULL)return 0; treenode* q[10];int f = -1, r = -1;//f頭結點，r尾結點int l = 0, ans = 0;//l每次指向每層的最后一個結點q[++r] = *t;treenode* p;while (f < r){p = q[++f];//隊列元素出隊，正在訪問的結點if (p->lchild)q[++r] = p->lchild;//左孩子入隊if (p->rchild)q[++r] = p->rchild;//右孩子入隊if (f == l)//處理該層的最右結點{ans++;//層數+1l = r;//讓l指向下一層}}return ans;
}

完整測試代碼

#include<stdio.h>  
#include<stdlib.h>  
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode, * tree;
void buildtree(tree* t)//建樹
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
int deep(tree* t)//求樹的深度
{if ((*t) == NULL)return 0; treenode* q[10];int f = -1, r = -1;//f頭結點，r尾結點int l = 0, ans = 0;//l每次指向每層的最后一個結點q[++r] = *t;treenode* p;while (f < r){p = q[++f];//隊列元素出隊，正在訪問的結點if (p->lchild)q[++r] = p->lchild;//左孩子入隊if (p->rchild)q[++r] = p->rchild;//右孩子入隊if (f == l)//處理該層的最右結點{ans++;//層數+1l = r;//讓l指向下一層}}return ans;
}
int main()
{tree t;buildtree(&t);printf("樹的高度為：%d\n", deep(&t)); return 0;
}
/*			AB        CD     E  F    */
//ABD##E##CF###

?6.設一棵二叉樹中各結點的值互不相同，其先序遍歷序列和中序遍歷序列分別存于兩個一維數組A[l...n]和 B[l...n]中，試編寫算法建立該二叉樹的二叉鏈表。

?本題代碼如下

tree build(char a[], char b[], int s, int e)
{if (s <= e){treenode* root = (treenode*)malloc(sizeof(treenode));root->data = a[pos];//將子樹的根節點賦值給rootint i;for (i = s; i <= e; i++)//在b數組中找到根節點if (b[i] == root->data)break;pos++;root->lchild = build(a, b, s, i - 1);//建立左子樹root->rchild = build(a, b, i + 1, e);//建立右子樹return root;}return NULL;
}

完整測試代碼

#include<stdio.h>
typedef struct treenode {char data;struct treenode* lchild, * rchild;
}treenode,*tree;
int pos = 0;//全局變量pos
tree build(char a[], char b[], int s, int e)
{if (s <= e){treenode* root = (treenode*)malloc(sizeof(treenode));root->data = a[pos];//將子樹的根節點賦值給rootint i;for (i = s; i <= e; i++)//在b數組中找到根節點if (b[i] == root->data)break;pos++;root->lchild = build(a, b, s, i - 1);//建立左子樹root->rchild = build(a, b, i + 1, e);//建立右子樹return root;}return NULL;
}
void disp(tree t)
{if (t){disp(t->lchild);disp(t->rchild);printf("%c", t->data);}
}
int main(){char a[] = {'A','B','D','E','C','F'};//先序char b[] = {'D','B','E','A','F','C' };//中序tree root = build(a, b, 0, 5);printf("后序序列為:");disp(root);return 0;
}

?7.二叉樹按二叉鏈表形式存儲，寫一個判別給定二叉樹是否是完全二叉樹的算法

?采用層次遍歷算法，將所有結點加入隊列(包括空結點)。

如果沒有左孩子，就看有沒有右孩子，如果有右孩子，那么不為完全二叉樹。

如果有左孩子，且之前不存在缺孩子的結點，左孩子進隊，如果有右孩子，右孩子也進隊，否則就是缺孩子了。之前存在缺孩子的，那么就不是完全二叉樹。

有兩種代碼的寫法

本題代碼如下

int isok(tree* t)//判斷完全二叉樹
{squene q;q.f = q.r = q.tag = 0;int flag = false; // 標志是否遇到了空節點if (*t == NULL)return true; // 空樹也是完全二叉樹enquene(&q, *t);treenode* p;while (!isempty(&q)){dequene(&q, &p);if (p->lchild){if (flag) // 如果之前遇到了空節點，說明不是完全二叉樹return false;enquene(&q, p->lchild);}else{flag = true;}if (p->rchild){if (flag) // 如果之前遇到了空節點，說明不是完全二叉樹return false;enquene(&q, p->rchild);}else{flag = true;}}return true;
}

完整測試代碼

#include <stdio.h>
#include <stdlib.h>
#define Max 15
#define true 1
#define false 0
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
} treenode, * tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
typedef struct squene
{struct treenode* data[Max];int f, r, tag;
} squene;
int isempty(squene* q)//判斷隊空
{if (q->f == q->r && q->tag == 0)return true;return false;
}
int isfull(squene* q)//判斷隊滿
{if (q->f == q->r && q->tag == 1)return true;return false;
}
int enquene(squene* q, treenode* p)//進隊操作
{if (isfull(q))return false;q->data[q->r] = p;q->r = (q->r + 1) % Max;q->tag = 1;return true;
}
int dequene(squene* q, treenode** p)//出隊操作
{if (isempty(q))return false;*p = q->data[q->f];q->f = (q->f + 1) % Max;q->tag = 0;return true;
}
int isok(tree* t)//判斷完全二叉樹
{squene q;q.f = q.r = q.tag = 0;int flag = false; // 標志是否遇到了空節點if (*t == NULL)return true; // 空樹也是完全二叉樹enquene(&q, *t);treenode* p;while (!isempty(&q)){dequene(&q, &p);if (p->lchild){if (flag) // 如果之前遇到了空節點，說明不是完全二叉樹return false;enquene(&q, p->lchild);}else{flag = true;}if (p->rchild){if (flag) // 如果之前遇到了空節點，說明不是完全二叉樹return false;enquene(&q, p->rchild);}else{flag = true;}}return true;
}
int main()
{treenode* t;buildtree(&t);if (isok(&t))printf("yes");elseprintf("no");return 0;
}

用ABD##E##CF##G##測試

/*? ? ? ? ? ? ? ? A

? ? ? ? B? ? ? ? ? ? ? ? C

D? ? ? ? E? ? ? ? F? ? ? ? G? ? ??

*/

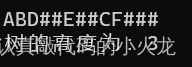
用ABD###CF##G##測試

/*? ? ? ? ? ? ? ? A

? ? ? ? B? ? ? ? ? ? ? ? C

D? ? ? ? ? ? ? ? ? F? ? ? ? G

*/

還可以用另外一種寫法

#include <stdio.h>
#include <stdlib.h>
#define Max 15
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
} treenode, * tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}int isok(tree* t)//判斷完全二叉樹
{treenode* q[Max];int f = -1, r = -1;int tag = 1;//標記是否為完全二叉樹q[++r] = *t;treenode* p;int flag = 1;//標記缺孩子if (*t == NULL) {tag = 1;}if (!(*t)->lchild && !(*t)->rchild)tag = 1;while (f < r) {p = q[++f];if (!p->lchild) //沒有左孩子缺孩子{flag = 0;if (p->rchild)tag = 0;}else//有左孩子{if (flag)//之前不存在缺孩子的結點{q[++r] = p->lchild;if (p->rchild)q[++r] = p->rchild;elseflag = 0;}else//之前存在缺孩子的結點tag = 0;}}if (tag)return 1;return 0;
}
int main()
{treenode* t;buildtree(&t);if (isok(&t))printf("yes");elseprintf("no");return 0;
}

用ABD##E##CF##G##

/*? ? ? ? ? ? ? ? A

? ? ? ? B? ? ? ? ? ? ? ? C

D? ? ? ? E? ? ? ? F? ? ? ? G? ? ??

*/

測試結果為

用AB#E##CF###

/*? ? ? ? ? ? ? ? A

? ? ? ? B? ? ? ? ? ? ? ? C

? ? ? ? ? ? E? ? ? ? F? ?

*/

測試結果為

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/211909.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/211909.shtml
英文地址，請注明出處：http://en.pswp.cn/news/211909.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

普冉（PUYA）單片機開發筆記(7): ADC-輪詢式多路采樣

普冉（PUYA）單片機開發筆記(7): ADC-輪詢式多路采樣

概述 應用中經常會有使用單片機進行模數轉換的需求。PY32F003 具有 1 個 12 位的模擬數字轉換器&#xff08;ADC&#xff09;&#xff0c;今天我們一起來使用一下這個 ADC。 數據手冊中對 ADC 簡介如下。 SAR ADC&#xff1a;逐次逼近式 ADC&#xff0c;原理參見“參考鏈接&a…
閱讀更多...
1830_emacs lisp的交互式模式

1830_emacs lisp的交互式模式

org-mode的標記語法 Grey 全部學習匯總&#xff1a; GitHub - GreyZhang/g_org: my learning trip for org-mode 交互式模式 emacs的交互式模式讓我對emacs的生命力有了更進一步的認識&#xff0c;但是我并沒有找到什么特別豐富的資料做這方面的學習與分析。尤其是理論與實…
閱讀更多...
class070 子數組最大累加和問題與擴展-上【算法】

class070 子數組最大累加和問題與擴展-上【算法】

class070 子數組最大累加和問題與擴展-上【算法】 code1 53. 最大子數組和 // 累加和最大子數組和 // 給你一個整數數組 nums // 請你找出一個具有最大累加和的非空子數組 // 返回其最大累加和 // 測試鏈接 : https://leetcode.cn/problems/maximum-subarray/ dp[i]&#xff…
閱讀更多...
【Docker】Docker Compose，yml 配置指令參考的詳細講解

【Docker】Docker Compose，yml 配置指令參考的詳細講解

作者簡介&#xff1a; 辭七七&#xff0c;目前大二&#xff0c;正在學習C/C&#xff0c;Java&#xff0c;Python等 作者主頁&#xff1a; 七七的個人主頁 文章收錄專欄&#xff1a; 七七的閑談 歡迎大家點贊 &#x1f44d; 收藏 ? 加關注哦&#xff01;&#x1f496;&#x1f…
閱讀更多...
基于c++版數據結構基于數組棧改-Python思維總結

基于c++版數據結構基于數組棧改-Python思維總結

##棧部分-&#xff08;疊貓貓&#xff09; ##抽象數據類型棧的定義&#xff1a;是一種遵循先入后出的邏輯的線性數據結構。 換種方式去理解這種數據結構如果我們在一摞盤子中取到下面的盤子&#xff0c;我們首先要把最上面的盤子依次拿走&#xff0c;才可以繼續拿下面的盤子&…
閱讀更多...
【Java期末復習資料】（2）常見例題 //持續更新

【Java期末復習資料】（2）常見例題 //持續更新

本文章主要是常見例題&#xff0c;解析不會太詳細&#xff0c;有問題、不會的可以給我發消息哦&#xff0c;后續會出模擬卷 常見例題&#xff1a; 1.下列跟Java技術平臺有關的是&#xff08;ABD&#xff09; A.JVM B.JDK C.JPN D.JRE 2.面向對象的特征包括&#xff08;ACD&…
閱讀更多...
wxPython的控件tree

wxPython的控件tree

wxPython樹控件介紹 樹&#xff08;tree&#xff09;是一種通過層次結構展示信息的控件&#xff0c;如下圖所示是樹控件示例&#xff0c;左窗口中是樹控件&#xff0c;在wxPython中樹控件類是wx.TreeCtrl。 wx.TreeCtrl常用的方法有 AddRoot(text, image-1, selImage-1, data…
閱讀更多...
在Deepin中安裝x11vnc工具并結合內網穿透軟件實現遠程訪問桌面

在Deepin中安裝x11vnc工具并結合內網穿透軟件實現遠程訪問桌面

文章目錄 1. 安裝x11vnc2. 本地遠程連接測試3. Deepin安裝Cpolar4. 配置公網遠程地址5. 公網遠程連接Deepin桌面6. 固定連接公網地址7. 固定公網地址連接測試 x11vnc是一種在Linux系統中實現遠程桌面控制的工具&#xff0c;它的原理是通過X Window系統的協議來實現遠程桌面的展…
閱讀更多...
P4 Qt如何添加qss樣式表文件和添加圖片資源

P4 Qt如何添加qss樣式表文件和添加圖片資源

目錄 前言 01 添加圖片資源文件 02 添加qss文件 前言 &#x1f3ac; 個人主頁&#xff1a;ChenPi &#x1f43b;推薦專欄1: 《C_ChenPi的博客-CSDN博客》??? &#x1f525; 推薦專欄2: 《Qt基礎_ChenPi的博客-CSDN博客》??? &#x1f33a;本篇簡介 &#xff1a;這一章…
閱讀更多...
JVM Optimization Learning(六)

JVM Optimization Learning(六)

目錄 一、JVM Optimization 1、Shenandoah Shenandoah的使用方法 2、ZGC ZGC的版本更迭 ZGC的使用方法 ZGC的參數設置 3、JMH測試GC性能 一、JVM Optimization 1、Shenandoah Shenandoah是由Red Hat開發的一款低延遲的垃圾收集器&#xff0c;Shenandoah并發執行大部分…
閱讀更多...
機器人純阻抗控制接觸剛性環境（阻尼影響因素）

機器人純阻抗控制接觸剛性環境（阻尼影響因素）

問題描述 在機器人學中&#xff0c;阻抗控制是一種常用的控制策略&#xff0c;用于管理機器人在與環境交互時的運動和力。阻抗控制背后的關鍵概念是將環境視為導納&#xff0c;而將機器人視為阻抗。 純阻抗控制接觸剛性環境時&#xff0c;機器人的行為方式主要受其阻抗參數的…
閱讀更多...
數據結構和算法專題---6、定時算法與應用

數據結構和算法專題---6、定時算法與應用

本章我們會對定時算法做個簡單介紹&#xff0c;包括常用的定時算法&#xff08;最小堆、時間輪&#xff09;的概述、實現方式、典型場景做個說明。 概述 系統或者項目中難免會遇到各種需要自動去執行的任務&#xff0c;實現這些任務的手段也多種多樣&#xff0c;如操作系統的…
閱讀更多...
【C++】使用“/**/“進行注釋的好處

【C++】使用“/**/“進行注釋的好處

2023年12月10日&#xff0c;周日晚上 我今天下午看Google Chrome的源碼時&#xff0c;才發現"/**/"原來還能這么用 使用"/**/"的好處就是&#xff0c;可以在任何地方進行注釋&#xff0c;哪怕是參數列表 void CircularWindow::enterEvent(QEvent *event/…
閱讀更多...
【Python】判斷域名是否合法

【Python】判斷域名是否合法

python判斷域名是否合法|校驗域名 域名以點號分隔成多個字符串。單個字符串由各國文字的特定字符集、字母、數字、連字符&#xff08;-&#xff09;組成&#xff0c;字母不區分大小寫&#xff0c;連字符&#xff08;-&#xff09;不得出現在字符串的頭部或者尾部。單個字符串長…
閱讀更多...
GitHub Enterprise Server 添加代碼安全、自動化功能

GitHub Enterprise Server 添加代碼安全、自動化功能

GitHub的軟件更新用于管理私有服務器上的存儲庫&#xff0c;具有GitHub容器注冊訪問、Dependabot安全警報和更新以及可重用工作流的特性。 GitHub Enterprise Server 3.5是GitHub用于托管和管理私有服務器上存儲庫的最新版本&#xff0c;它引入了新的代碼安全特性&#xff0c;新…
閱讀更多...
Helm 常用運維命令

Helm 常用運維命令

原理參考 ## https://blog.csdn.net/knight_zhou/article/details/122079292 常用運維命令 helm search: ??搜索charthelm pull: ???下載chart到本地目錄查看helm install: ??上傳chart到Kuberneteshelm list: ????列出已發布的chart
閱讀更多...
【開源】基于Vue和SpringBoot的車險自助理賠系統

【開源】基于Vue和SpringBoot的車險自助理賠系統

項目編號&#xff1a; S 018 &#xff0c;文末獲取源碼。 \color{red}{項目編號&#xff1a;S018&#xff0c;文末獲取源碼。} 項目編號&#xff1a;S018&#xff0c;文末獲取源碼。 目錄 一、摘要1.1 項目介紹1.2 項目錄屏 二、功能模塊2.1 數據中心模塊2.2 角色管理模塊2.3 車…
閱讀更多...
Maven基礎

Maven基礎

目錄 Maven坐標 坐標簡介 主要組成 Maven依賴管理 配置依賴 依賴簡介 配置依賴 依賴傳遞 依賴傳遞簡介 排除依賴 依賴范圍 生命周期 生命周期簡介 執行指定生命周期 Maven坐標 坐標簡介 Maven中的坐標是資源的唯一標識&#xff0c;通過該坐標可以唯一定位資…
閱讀更多...
Redis交互速度慢，CPU占用100%，集群方案，報錯等問題

Redis交互速度慢，CPU占用100%，集群方案，報錯等問題

后續補充結論 仔細查看前輩們堆的代碼中發現居然調用了大量key*查詢&#xff0c;導致走的遍歷非常慢&#xff01;因為這相當與全部數據量遍歷&#xff0c;即這個原因導致了查詢速度與數據量成正比&#xff0c;推測也是CPU占用高的元兇&#xff1b;即使加上key前綴再匹配*也會走…
閱讀更多...
Python開發運維：Python調用K8S API實現資源管理

Python開發運維：Python調用K8S API實現資源管理

目錄 一、實驗 1.Python操作K8S API獲取資源 2.Python操作K8S API創建deployment資源 3.Python操作K8S API刪除k8s資源 4.Python操作K8S API修改k8s資源 5.Python操作K8S API查看k8s資源 二、問題 1.Windows11安裝kubernetes報錯 2.Python通過調用哪些方法實現Pod和De…
閱讀更多...
最新文章

Copyright @ 2022~2023