0. 前言

單獨用一篇文章來講解VINS-MONO中的marginalization。

為什么要marg
什么是marg

1.1 Marginalization Pipiline

本文著重講解MARGIN_OLD部分，MARGIN_NEW部分很簡單。

1. marg factor構建

marg_factor、ResidualBlockInfo、marg_info、ceres::problem的調用關系：

ceres::problem是整個系統的優化，在optimization()前半部分進行的，其中第一個AddResidualBlock調用的就是上一次marg的結果，即這次優化的先驗，重點是理解last_marginalization_info，下面會詳細介紹。

marg部分的信息矩陣由3部分構成：先驗，IMU，視覺。程序里對應factor

針對每一部分factor，處理部分都是三板斧：

• 定義3種factor：MarginalizationFactor，IMUFactor，ProjectionTdFactor(ProjectionFactor)
• 構建ResidualBlockInfo
• 把addResidualBlockInfo加入到MarginalizationInfo中

分別在1.2~1.4節對這三板斧進行拆解。

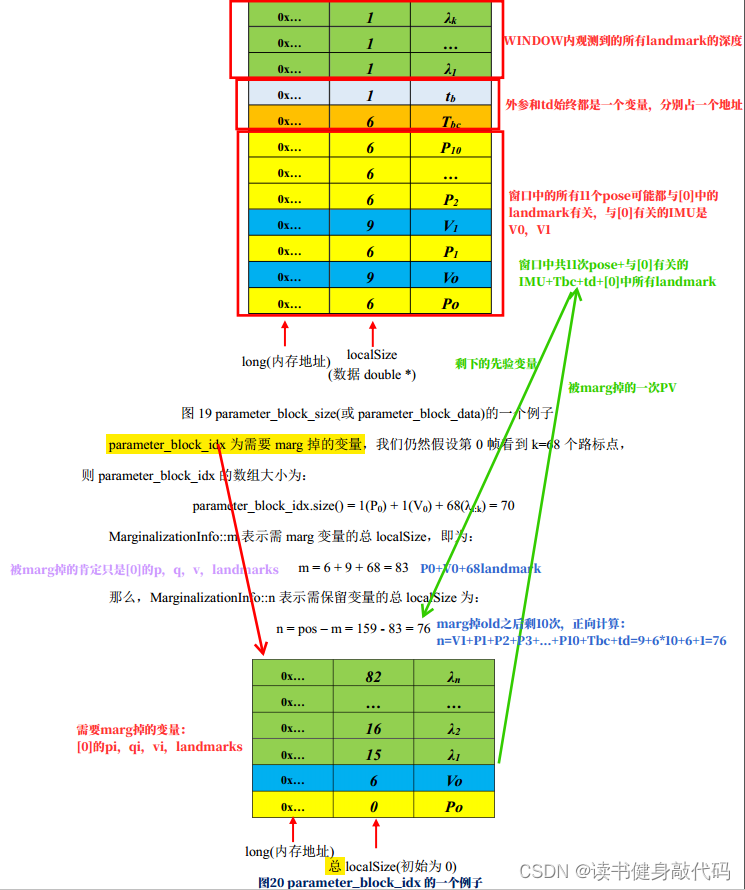
1.1 變量及維度理解

變量名	說明
marginalization_info	保存marg的先驗等信息
parameter_block_size	<與marg幀相關的優化變量內存地址,localSize>
parameter_block_idx	<與marg幀相關的優化變量內存地址, idx> (前m維是marg，后n維是remain)
parameter_block_data	<與marg幀相關的優化變量內存地址,數據>
keep_block_data	keep_開頭均與remain相關
m	所有將被marg掉變量的localsize之和
n	所有與將被marg掉變量有約束關系的變量的localsize之和
n	所有與將被marg掉變量有約束關系的變量的localsize之和

結合崔華坤PDF的解釋來理解：

解釋一下MARGIN_OLD為什么有11個P，因為old觀測到的landmark可能被WINDOW內的pose都觀測到了，marg掉old的視覺觀測會對后面的視覺pose產生約束信息，所以都有residual邊，所以11個都要。

在ResidualBlockInfo的Evaluate()中進行維度debug

ROS_DEBUG_STREAM("\ncost_function->num_residuals(): " << cost_function->num_residuals() <<"\ncost_function->parameter_block_sizes().size: " << cost_function->parameter_block_sizes().size());
for(int i=0; i<cost_function->parameter_block_sizes().size(); ++i) {ROS_DEBUG("\nparameter_block_sizes()[%d]: %d", i, cost_function->parameter_block_sizes()[i]);
}

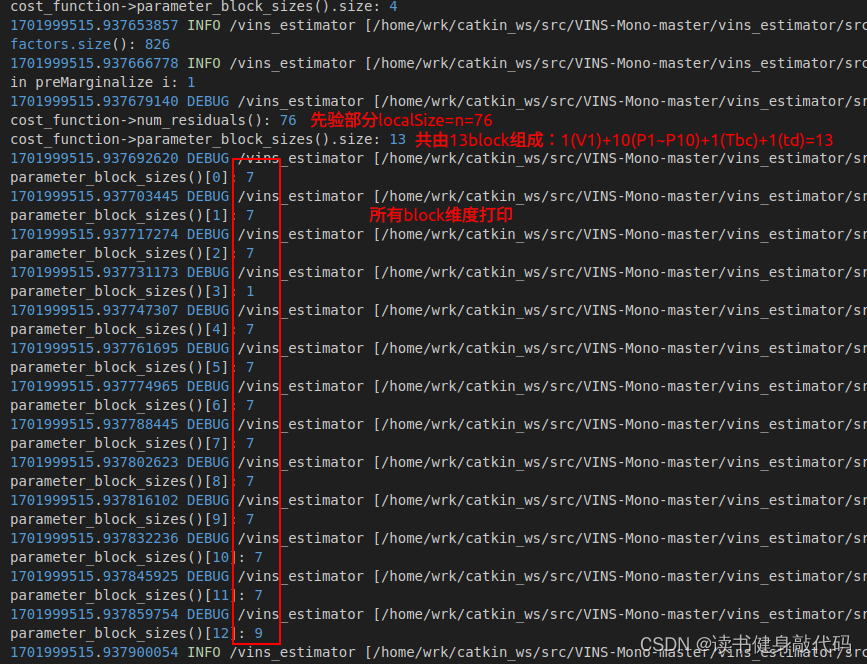
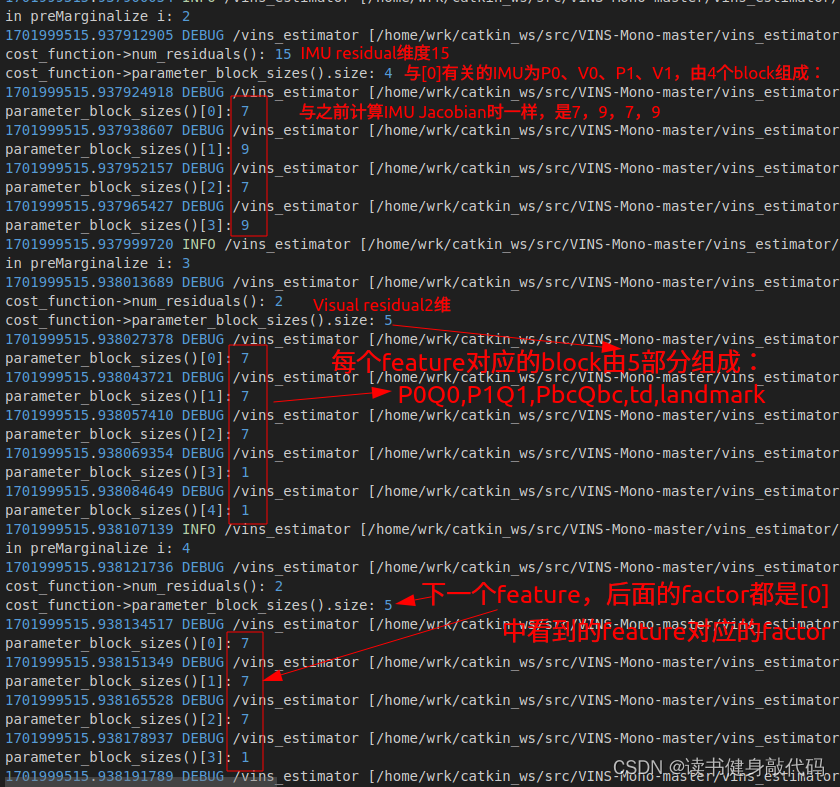
PS：后續的P的localSize函數會將維度7改為6。

1.2 IMUFactor

對應論文整體的cost function來理解

1.3 ProjectionTdFactor(ProjectionFactor)

同IMU factor。

1.4 MarginalizationFactor($e_p$推導更新，FEJ解決的問題)

繼承ceres::CostFunction的一個類，與前面兩個factor是同一類型的類。

不同的factor是不同的類，但factor均繼承ceres::CostFunction，不同factor調用evaluate()的是其各自的虛函數，屬于多態。

定義了新的factor就要考慮residual如何計算、殘差塊的Jacobian如何計算，MarginalizationFactor中重載的虛函數Evaluate()就完成了先驗殘差$e_p$和先驗Jacobian的更新，在1.4.1和1.4.2節詳細介紹。

代碼注釋：

//先驗部分的factor，求Jacobian
bool MarginalizationFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{int n = marginalization_info->n;int m = marginalization_info->m;Eigen::VectorXd dx(n);for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++){int size = marginalization_info->keep_block_size[i];int idx = marginalization_info->keep_block_idx[i] - m;//因為當時存的是marg時的idx，是在m后面的，現在單看先驗塊的話就需要減去m//優化后，本次marg前的待優化變量Eigen::VectorXd x = Eigen::Map<const Eigen::VectorXd>(parameters[i], size);//優化前，上次maerg后的變量，即Jacobian的線性化點x0Eigen::VectorXd x0 = Eigen::Map<const Eigen::VectorXd>(marginalization_info->keep_block_data[i], size);//求優化后的變量與優化前的差，dx即公式中的δxp。//IMU block、landmark depth bolck直接相減，而camera pose block的rotation部分需使用四元數計算δxpif (size != 7)dx.segment(idx, size) = x - x0;else{//translation直接相減dx.segment<3>(idx + 0) = x.head<3>() - x0.head<3>();//rotation部分：δq=[1, 1/2 delta theta]^T(為何非要取正的？)dx.segment<3>(idx + 3) = 2.0 * Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();if (!((Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).w() >= 0)){dx.segment<3>(idx + 3) = 2.0 * -Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();}}}//更新誤差：f' = f + J*δxpEigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;//Jacobian保持不變（FEJ要解決這樣做帶來的解的零空間變化的問題）if (jacobians){for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++){if (jacobians[i]){int size = marginalization_info->keep_block_size[i], local_size = marginalization_info->localSize(size);int idx = marginalization_info->keep_block_idx[i] - m;Eigen::Map<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobian(jacobians[i], n, size);jacobian.setZero();jacobian.leftCols(local_size) = marginalization_info->linearized_jacobians.middleCols(idx, local_size);}}}return true;
}

1.4.1 先驗殘差的更新

本次solve后需要更新先驗殘差$e_p$，如何更新呢？

先上結論：$$e_p=e_0+J_l?dx$$

• $e_0$是上次marg之后從信息矩陣和b中反解出來的residual，
• $J_l$是上次反解出來的Jacobian
• dx是這次優化后，這次marg時的變量$x$與上次marg時變量$x_0$(也即下文提到的線性化點)的差，理解為$dx=x_k?x_{k?1}$

---

精簡版推導（需要看）：

---

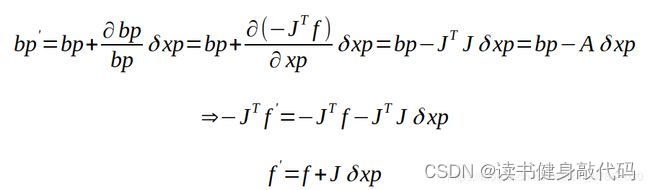
復雜版推導(可以跳過不看)：

以下關于marg的推導截圖自博客：

上述推導簡單總結如下，發現了FEJ解決的問題所在：

1.4.2 先驗Jacobian的更新

從代碼中可以看出先驗的Jacobian沒有改變，仍然使用上一時刻的Jacobian，下面介紹為什么。

系統中兩處使用到了先驗的Jacobian：

1. 本次solve時加入了先驗（last_marginalization_info）factor對應的ResidualBlock，ceres執行solve需要使用先驗的Jacobian
2. 在執行marg時，構建信息矩陣也需要先驗Jacobian

整體系統的Jacobian就一個，維度是pos*pos，只是我們某個factor部分的Jacobian的話，維度會比pos*pos小一點，這是因為其他一些無關變量不會算在部分的Jacobian中（如IMU的$b^a$就與視覺residual無關，計算視覺Jacobian時就沒有關于$b^a$的部分），但是需要明確，整個系統就一個大的pos*pos的jacobian，相應的信息矩陣也就一個，只不過優化會導致Jacobian的值發生變化，而marg會導致優化變量發生變化，進而Jacobian也變化，但是需要清楚的是，我們從始至終維護的都只是這一個大的Jacobian.

在講如何求先驗的Jacobian之前，需要鋪墊一下線性化點的相關內容：

記上次優化后的變量為$x_0$，對應的Jacobian是$J_l$，本次優化后的變量為$x^{\prime }$，對應的Jacobian是$J^{\prime }$，在程序中我們令$J^{\prime }=J_l$

$J^{\prime }$理應是residual對$x^{\prime }$求導獲得，但由于$x_0$中的一些變量(P0,V0,landmark等)已經在上次marg時被marg掉了，所以$x^{\prime }$已經不是$x_0$了，但我們仍然讓$J^{\prime }=J_l$。線性化點發生了變化，但Jacobian沒變(從last_marginalization_info的信息矩陣中反解出來的)，這就會導致$x$的零空間發生變化，而FEJ算法解決的就是這個問題，只不過在VINS中沒有使用，VINS認為對于小誤差是有tolerance的。崔華坤PDF6.4節對于此部分有做討論，可以去看看。

---

2. ResidualBlockInfo構建

這部分主要關注drop_set的表意：指定傳入的_parameter_blocks中哪些是需要被marg的。

1. 先驗factor：old的P（para_Pose[0]），V（para_SpeedBias[0]）
2. IMU factor：old的P（para_Pose[0]），V（para_SpeedBias[0]）
3. Visual factor：old的P（para_Pose[0]），從old開始觀測的landmark（para_Feature[feature_index]）

剛開始看代碼時有個愚蠢的疑問，我們要marg的變量是通過傳入drop_set來指定的，那為什么不直接傳入marg的變量？為什么在代碼中構建ResidualBlockInfo時還要傳入P[1]V[1]這些remain的變量？原因是
4. 如果不傳，就不能復用之前定義的IMU和視覺的factor，需要重寫不含remain的factor，重推Jacobian等。
5. 也是最重要的一點，在后面構建marg信息矩陣時需要用到residual對于remain變量來說，它們需要接受marg幀傳遞信息，也即需要residual對remain的Jacobian，肯定要將remain變量傳入。

3. addResidualBlockInfo()加入到MarginalizationInfo中

該函數完成兩件事：

1. 把每個factor中待優化參數的維度傳給parameter_block_size，建立 地址->size 的映射（eg：IMU factor的_parameter_blocks共有4個P0，V0，P1，V1：size分別是7，9，7，9，剩下的看Debug圖理解即可）
2. 為要marg的變量占key的座，值為0。在marginalize()中是否有key來區分marg和remain變量。

再貼一下1.1節的debug結果，現在理解就很容易了：

代碼注釋如下：

void MarginalizationInfo::addResidualBlockInfo(ResidualBlockInfo *residual_block_info)
{factors.emplace_back(residual_block_info);std::vector<double *> &parameter_blocks = residual_block_info->parameter_blocks;//每個factor的待優化變量的地址std::vector<int> parameter_block_sizes = residual_block_info->cost_function->parameter_block_sizes();//待優化變量的維度//parameter_blocks.size//有td時，先驗factor為13(9*1+6*10+6+1)，IMU factor為4(7,9,7,9)，每個feature factor size=5(7,7,7,1)//無td時             12                           4                                  4for (int i = 0; i < static_cast<int>(residual_block_info->parameter_blocks.size()); i++){double *addr = parameter_blocks[i];int size = parameter_block_sizes[i];//待優化變量的維度//map沒有key時會新建key-value對parameter_block_size[reinterpret_cast<long>(addr)] = size;//global size <優化變量內存地址,localSize>}//需要 marg 掉的變量for (int i = 0; i < static_cast<int>(residual_block_info->drop_set.size()); i++){double *addr = parameter_blocks[residual_block_info->drop_set[i]];//獲得待marg變量的地址//要marg的變量先占個key的座，marg之前將m放在一起，n放在一起parameter_block_idx[reinterpret_cast<long>(addr)] = 0;//local size <待邊緣化的優化變量內存地址,在parameter_block_size中的id>，}
}

4. preMarginalize()

代碼注釋：

void MarginalizationInfo::preMarginalize()
{
//    ROS_INFO_STREAM("\nfactors.size(): " << factors.size());int i=0;for (auto it : factors){
//        ROS_INFO_STREAM("\nin preMarginalize i: "<< ++i);  //很大，能到900多，說明[0]觀測到了很多landmarkit->Evaluate();//計算每個factor的residual和Jacobianstd::vector<int> block_sizes = it->cost_function->parameter_block_sizes(); //residual總維度，先驗=last n=76，IMU=15，Visual=2for (int i = 0; i < static_cast<int>(block_sizes.size()); i++){long addr = reinterpret_cast<long>(it->parameter_blocks[i]);//parameter_blocks是vector<double *>，存放的是數據的地址int size = block_sizes[i];//如果優化變量中沒有這個數據就new一片內存放置if (parameter_block_data.find(addr) == parameter_block_data.end()){double *data = new double[size];//dst,srcmemcpy(data, it->parameter_blocks[i], sizeof(double) * size);parameter_block_data[addr] = data;}}}
}

4.1 ResidualBlockInfo::Evaluate()

在info添加完所有的factor(先驗，IMU，視覺)之后，分別求各個factor的residual和Jacobian，先驗部分的residual和Jacobian的更新在1.4節已經講解。

cost_function->Evaluate()是典型的多態。

4.2 魯棒核函數

針對各個factor，如果傳入了魯棒核函數loss_function，則需要對residual和jacobian進行加權，簡言之，計算權值并與residual、Jacobian相乘。

if (loss_function)
{double residual_scaling_, alpha_sq_norm_;double sq_norm, rho[3];sq_norm = residuals.squaredNorm();//loss_function 為 robust kernel function，in：sq_norm， out：rho  out[0] = rho(sq_norm),out[1] = rho'(sq_norm), out[2] = rho''(sq_norm),loss_function->Evaluate(sq_norm, rho);//求取魯棒核函數關于||f(x)||^2的一二階導數//printf("sq_norm: %f, rho[0]: %f, rho[1]: %f, rho[2]: %f\n", sq_norm, rho[0], rho[1], rho[2]);double sqrt_rho1_ = sqrt(rho[1]);if ((sq_norm == 0.0) || (rho[2] <= 0.0)){residual_scaling_ = sqrt_rho1_;alpha_sq_norm_ = 0.0;}else{const double D = 1.0 + 2.0 * sq_norm * rho[2] / rho[1];//求根公式的△const double alpha = 1.0 - sqrt(D);//求根公式求方程的根residual_scaling_ = sqrt_rho1_ / (1 - alpha);alpha_sq_norm_ = alpha / sq_norm;}for (int i = 0; i < static_cast<int>(parameter_blocks.size()); i++){jacobians[i] = sqrt_rho1_ * (jacobians[i] - alpha_sq_norm_ * residuals * (residuals.transpose() * jacobians[i]));}residuals *= residual_scaling_;
}

帶robust kernel function的Jacobian，總體思想是：用robust kernel function計算一個scale，用于對原residual進行縮放，對Jacobian進行加權，ceres官方文檔如下圖，參考自

對theory進行簡單推導以理解代碼

上述theory中重要的是核函數關于$||f(x)|{|}^2$的一二階導數，和$\alpha$的求解，導數部分調用loss_function->Evaluate即可，我們需要手動求解$\alpha$，對于公式
$$\frac{1}{2}{\alpha }^2?\alpha ?\frac{{\rho }^{\prime \prime }}{{\rho }^{\prime }}||f(x)|{|}^2=0$$
運用求根公式可求得$\alpha$，其中
$$\begin{array}{rl}& a=\frac{1}{2}\\ & b=?1\\ & c=?\frac{{\rho }^{\prime \prime }}{{\rho }^{\prime }}||f(x)|{|}^2\end{array}$$

所以$$\alpha =\frac{?b\pm \sqrt{b^2?4ac}}{2a}=\frac{1\pm \sqrt{1+2\frac{{\rho }^{\prime \prime }}{{\rho }^{\prime }}||f(x)|{|}^2}}{1}$$

代碼中D=$1+2\frac{{\rho }^{\prime \prime }}{{\rho }^{\prime }}||f(x)|{|}^2$

5. marginalize()

先上代碼注釋：

//線程函數
void* ThreadsConstructA(void* threadsstruct)
{ThreadsStruct* p = ((ThreadsStruct*)threadsstruct);//遍歷該線程分配的所有factors，所有觀測項for (auto it : p->sub_factors){//遍歷該factor中的所有參數塊P0，V0等for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++){int idx_i = p->parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];int size_i = p->parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])];if (size_i == 7) //對于pose來說，是7維的,最后一維為0，這里取左邊6size_i = 6;//只提取local size部分，對于pose來說，是7維的,最后一維為0，這里取左邊6維Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++){int idx_j = p->parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];int size_j = p->parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])];if (size_j == 7)size_j = 6;Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);//主對角線if (i == j)p->A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;//非主對角線else{p->A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;p->A.block(idx_j, idx_i, size_j, size_i) = p->A.block(idx_i, idx_j, size_i, size_j).transpose();}}p->b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;}}return threadsstruct;
}void MarginalizationInfo::marginalize()
{int pos = 0;//it.first是要被marg掉的變量的地址,將其size累加起來就得到了所有被marg的變量的總localSize=m//marg的放一起，共m維，remain放一起，共n維for (auto &it : parameter_block_idx){it.second = pos;//也算是排序1pos += localSize(parameter_block_size[it.first]);//PQ7為改為6維}m = pos;//要被marg的變量的總維度int tmp_n = 0;//與[0]相關總維度for (const auto &it : parameter_block_size){if (parameter_block_idx.find(it.first) == parameter_block_idx.end())//將不在drop_set中的剩下的維度加起來，這一步實際上算的就是n{parameter_block_idx[it.first] = pos;//排序2tmp_n += localSize(it.second);pos += localSize(it.second);}}n = pos - m;//remain變量的總維度，這樣寫建立了n和m間的關系，表意更強ROS_DEBUG("\nn: %d, tmp_n: %d", n, tmp_n);//ROS_DEBUG("marginalization, pos: %d, m: %d, n: %d, size: %d", pos, m, n, (int)parameter_block_idx.size());TicToc t_summing;Eigen::MatrixXd A(pos, pos);//總系數矩陣Eigen::VectorXd b(pos);//總誤差項A.setZero();b.setZero();//multi thread 構建信息矩陣和誤差項TicToc t_thread_summing;pthread_t tids[NUM_THREADS];//4個線程構建//攜帶每個線程的輸入輸出信息ThreadsStruct threadsstruct[NUM_THREADS];//將先驗約束因子平均分配到4個線程中int i = 0;//for (auto it : factors){threadsstruct[i].sub_factors.push_back(it);i++;i = i % NUM_THREADS;}//將每個線程構建的A和b加起來for (int i = 0; i < NUM_THREADS; i++){TicToc zero_matrix;threadsstruct[i].A = Eigen::MatrixXd::Zero(pos,pos);threadsstruct[i].b = Eigen::VectorXd::Zero(pos);threadsstruct[i].parameter_block_size = parameter_block_size;threadsstruct[i].parameter_block_idx = parameter_block_idx;int ret = pthread_create( &tids[i], NULL, ThreadsConstructA ,(void*)&(threadsstruct[i]));if (ret != 0){ROS_WARN("pthread_create error");ROS_BREAK();}}//將每個線程構建的A和b加起來for( int i = NUM_THREADS - 1; i >= 0; i--){pthread_join( tids[i], NULL );//阻塞等待線程完成A += threadsstruct[i].A;b += threadsstruct[i].b;}//ROS_DEBUG("thread summing up costs %f ms", t_thread_summing.toc());//ROS_INFO("A diff %f , b diff %f ", (A - tmp_A).sum(), (b - tmp_b).sum());/*求Amm的逆矩陣時，為了保證數值穩定性，做了Amm=1/2*(Amm+Amm^T)的運算，Amm本身是一個對稱矩陣，所以  等式成立。接著對Amm進行了特征值分解,再求逆，更加的快速*///數值計算中，由于計算機浮點數精度的限制，有時候數值誤差可能導致 Amm 不精確地保持對稱性。//通過將 Amm 更新為其本身與其轉置的平均值，可以強制保持對稱性，提高數值穩定性。這種對稱性維護的策略在數值計算中比較常見。Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);//ROS_ASSERT_MSG(saes.eigenvalues().minCoeff() >= -1e-4, "min eigenvalue %f", saes.eigenvalues().minCoeff());//marg的矩陣塊求逆,特征值分解求逆更快Eigen::MatrixXd Amm_inv = saes.eigenvectors()* Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal()* saes.eigenvectors().transpose();//printf("error1: %f\n", (Amm * Amm_inv - Eigen::MatrixXd::Identity(m, m)).sum());Eigen::VectorXd bmm = b.segment(0, m);Eigen::MatrixXd Amr = A.block(0, m, m, n);Eigen::MatrixXd Arm = A.block(m, 0, n, m);Eigen::MatrixXd Arr = A.block(m, m, n, n);Eigen::VectorXd brr = b.segment(m, n);//Shur compliment marginalization，求取邊際概率A = Arr - Arm * Amm_inv * Amr;b = brr - Arm * Amm_inv * bmm;//由于Ceres里面不能直接操作信息矩陣，所以這里從信息矩陣中反解出來了Jacobian和residual，而g2o是可以的，ceres里只需要維護H和bEigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);//對稱陣Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));//對稱陣的倒數陣Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));Eigen::VectorXd S_sqrt = S.cwiseSqrt();//開根號Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();//從H和b中反解出Jacobian和residuallinearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;

5.1 對marg和remain排序

parameter_block_idx在addResidualBlockInfo時有過占key座，此時可以用來對marg和remain變量排序，將marg變量放在一起，remain放在一起，marginalize()里這段代碼可以仔細欣賞一下。

5.1 信息矩陣與誤差的構建

代碼里使用多線程構建信息矩陣，將對不同變量的Jacobian根據parameter_block_idx和parameter_block_size放到相應的位置上去，
最終構建出下圖所示的A和b：

residual共有3種：先驗residual，IMU residual，Visual residual，而每個殘差只和某幾個狀態量相關，所以對于無關項的Jacobian直接為0，

組裝過程如下：

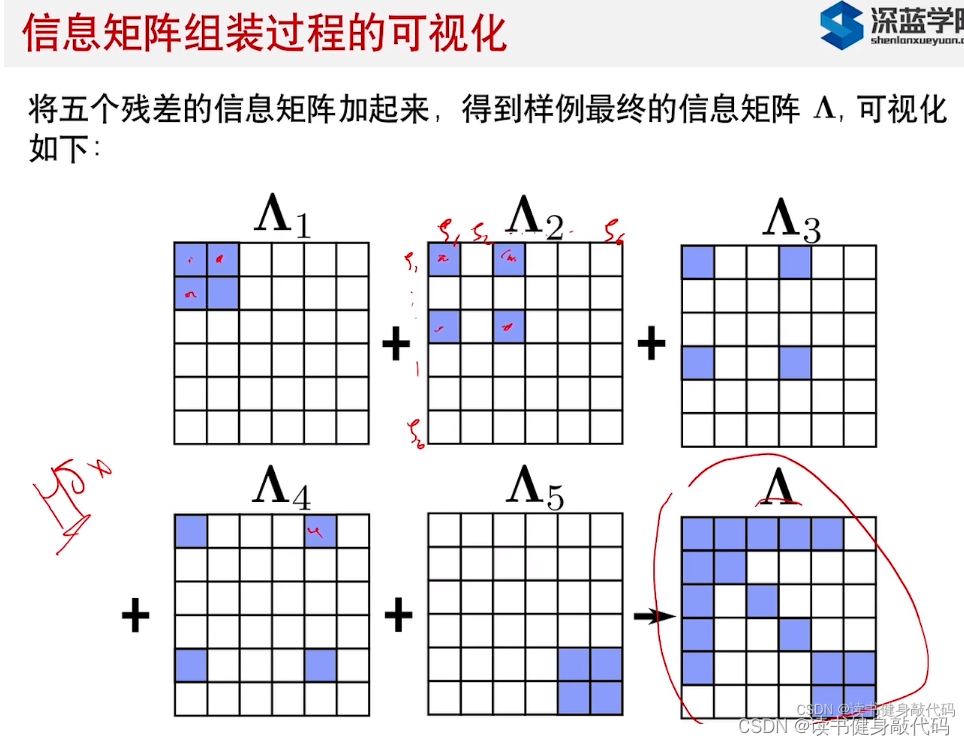
比如對于P0的信息矩陣，可能由上述3部分組成，而對于V0，可能由先驗和IMU residual組成，來自不同部分的需要+=

最終構建結果如下圖所示的形式：

5.2 Schur compliment

5.2.1 理論介紹

本部分理論詳細介紹可參考之前的博客

核心結論就一張圖：

5.2.2 兩個trick

這里使用了兩個trick：

1. 提高對稱陣Amm的數值穩定性
2. 特征值分解求解對稱陣的逆Amm_inv，加快求逆速度

//數值計算中，由于計算機浮點數精度的限制，有時候數值誤差可能導致 Amm 不精確地保持對稱性。
//通過將 Amm 更新為其本身與其轉置的平均值，可以強制保持對稱性，提高數值穩定性。這種對稱性維護的策略在數值計算中比較常見。
Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);//ROS_ASSERT_MSG(saes.eigenvalues().minCoeff() >= -1e-4, "min eigenvalue %f", saes.eigenvalues().minCoeff());//marg的矩陣塊求逆,特征值分解求逆更快
Eigen::MatrixXd Amm_inv = saes.eigenvectors()* Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal()* saes.eigenvectors().transpose();

GPT3.5：

1. Amm 的逆矩陣是通過特征值分解（Eigenvalue Decomposition）來求解的。特征值分解將對稱矩陣 Amm 分解為其特征向量和特征值的乘積，即 Amm = V * D * V^T，其中 V 是特征向量矩陣，D 是特征值對角矩陣。這樣，逆矩陣可以用特征值的倒數替換特征值，然后再乘以特征向量的轉置。
2. 特別地，這里使用了 Eigen::SelfAdjointEigenSolver，它是專門用于對稱矩陣的特征值分解的 Eigen 類。它返回特征值和特征向量，這樣就能夠輕松地進行逆矩陣的計算。
3. 為什么使用特征值分解來加速求逆的過程呢？特征值分解后的矩陣形式是對角矩陣，其逆矩陣可以直接通過將對角元素取倒數得到。這個過程相較于直接對原始矩陣進行逆運算，更為高效，尤其是對于大規模矩陣。

其中最難理解的這一句

Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal()

1. saes.eigenvalues().array() > eps：首先，對 saes 對象中的特征值數組執行逐元素比較，生成一個布爾類型的數組，其中對應位置的元素為 true 表示對應的特征值大于 eps，否則為 false。
2. .select(saes.eigenvalues().array().inverse(), 0)：接下來，使用 select 函數，根據上一步生成的布爾數組，在大于 eps 的位置選擇對應的特征值的倒數，否則選擇 0。這樣，小于等于 eps 的特征值都被替換為 0。
3. Eigen::VectorXd(…)：將上一步生成的數組轉換為 Eigen 庫中的列向量。
4. .asDiagonal()：將列向量轉換為對角矩陣，其中對角線上的元素為列向量中的元素，其他位置為零。

根據之前博客marg部分線性化點的討論，我們假設marg時線性化點為$x_0$，我們此時可以從J和residual中求解出$x_0$出對應的Jacobian和residual：

反解方法：

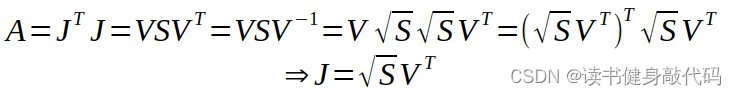
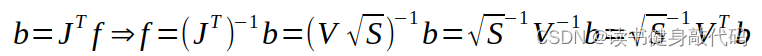
對應代碼：

//由于Ceres里面不能直接操作信息矩陣，所以這里從信息矩陣中反解出來了Jacobian和residual，而g2o是可以的，ceres里只需要維護H和b
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
//對稱陣
Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
//對稱陣的倒數陣
Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));Eigen::VectorXd S_sqrt = S.cwiseSqrt();//開根號
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();//從H和b中反解出Jacobian和residual
linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;

6. addr_shift 內存管理

關于addr_shift的理解

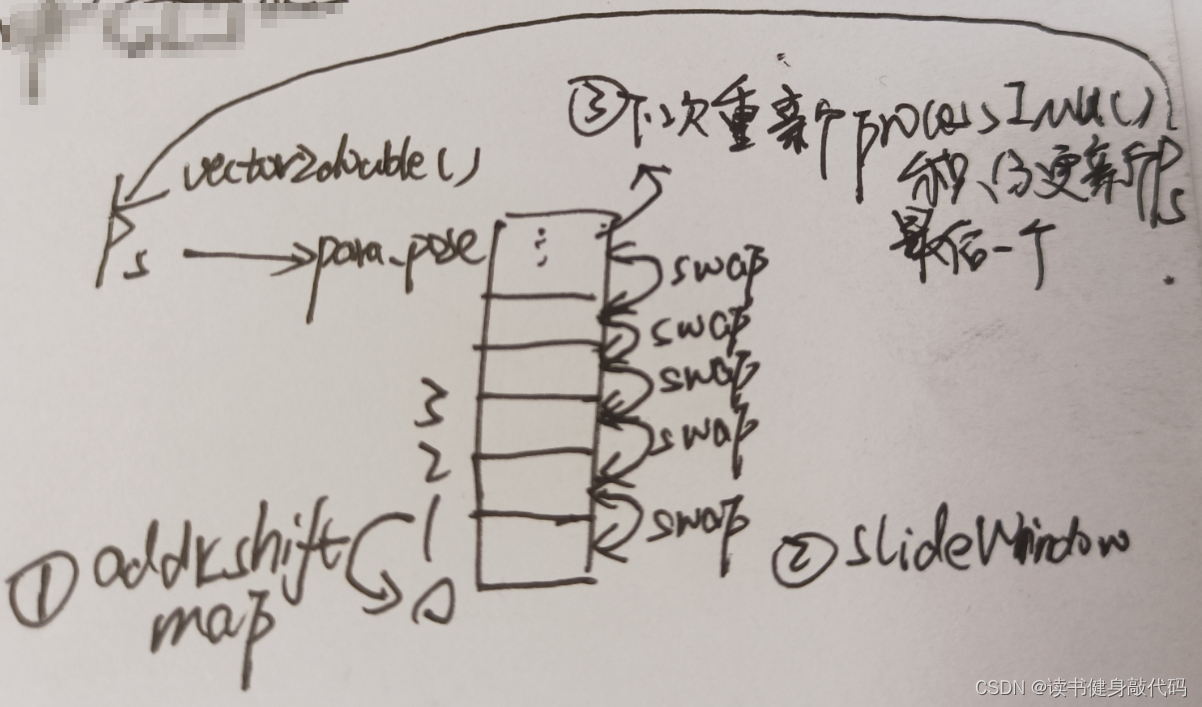
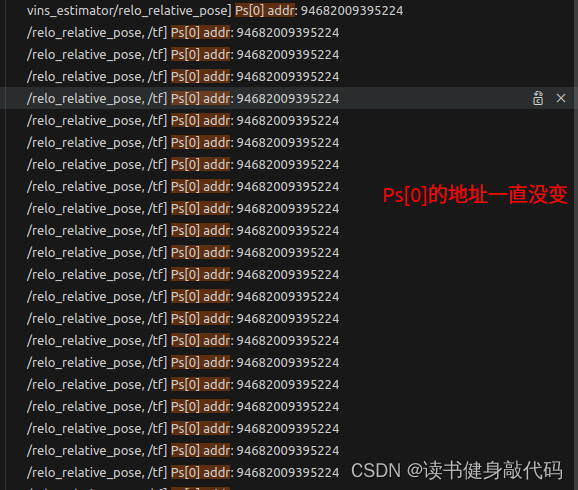
而addr_shift的意義就在于讓系統優化的變量的起始地址不變，如果有新的landmark加入則會使整個parameter block所占的內存增大一點，但是整塊內存的首地址是不變的，這樣避免了因不斷marg而導致的待優化變量的地址改變，進而導致地不斷delete舊內存和new新內存，可以在求解后的slideWindow后加上一句打印：

ROS_DEBUG("Ps[0] addr: %ld", reinterpret_cast<long>(&Ps[0]));

1. 地址操作完成之后，getParameterBlocks(addr_shift)整理本次marg結果，放在keep_xxx中。

2. 將本次marg結果傳遞，下次循環之后再optimization函數中就會將本次marg結果應用到整個系統的ResidualBlock中，如此optimize，marg，optimize循環

last_marginalization_info = marginalization_info;
last_marginalization_parameter_blocks = parameter_blocks;

7. slideWindow

7.1 整體代碼

根據之前KF selection的結果來執行不同的marg操作：

• MARGIN_OLD則將old(即WINDOW[0])冒泡到最右側(即WINDOW[WINDOW_SIZE])，刪掉其預積分，并將all_image_frame內第[0]幀到old所在幀范圍內(含)的所有frame刪掉。對于old幀，還應將該幀下的landmark深度值向后傳遞。
• MARGIN_SECOND_NEW則2nd繼承1st的IMU預積分，并初始化1st的預積分，all_image_frame不變

這部分之前在第3篇的2.2.3.7小結debug過一次，all_image_frame在長時間沒遇到KF時確實會存在buffer很多幀圖像的情況。

代碼和注釋：

void Estimator::slideWindow()
{TicToc t_margin;//把最老的幀冒泡移到最右邊，然后delete掉，在new一個新的對象出來if (marginalization_flag == MARGIN_OLD){double t_0 = Headers[0].stamp.toSec();back_R0 = Rs[0];back_P0 = Ps[0];if (frame_count == WINDOW_SIZE){for (int i = 0; i < WINDOW_SIZE; i++)//循環完成也就冒泡完成到最右側{Rs[i].swap(Rs[i + 1]);//世界系下old冒泡std::swap(pre_integrations[i], pre_integrations[i + 1]);//每一幀的預積分old冒泡dt_buf[i].swap(dt_buf[i + 1]);//各種buf也冒泡linear_acceleration_buf[i].swap(linear_acceleration_buf[i + 1]);angular_velocity_buf[i].swap(angular_velocity_buf[i + 1]);Headers[i] = Headers[i + 1];//最后一個是 Headers[WINDOW_SIZE-1] = Headers[WINDOW_SIZE]Ps[i].swap(Ps[i + 1]);Vs[i].swap(Vs[i + 1]);Bas[i].swap(Bas[i + 1]);Bgs[i].swap(Bgs[i + 1]);}//這一步是為了 new IntegrationBase時傳入最新的預積分的初值acc_0, gyr_0，ba，bg，所以必須要強制等于最新的Headers[WINDOW_SIZE] = Headers[WINDOW_SIZE - 1];Ps[WINDOW_SIZE] = Ps[WINDOW_SIZE - 1];Vs[WINDOW_SIZE] = Vs[WINDOW_SIZE - 1];Rs[WINDOW_SIZE] = Rs[WINDOW_SIZE - 1];Bas[WINDOW_SIZE] = Bas[WINDOW_SIZE - 1];Bgs[WINDOW_SIZE] = Bgs[WINDOW_SIZE - 1];//冒泡到最右邊之后把對應的都delete&new或者clear掉delete pre_integrations[WINDOW_SIZE];//delete掉，并new新的預積分對象出來pre_integrations[WINDOW_SIZE] = new IntegrationBase{acc_0, gyr_0, Bas[WINDOW_SIZE], Bgs[WINDOW_SIZE]};dt_buf[WINDOW_SIZE].clear();linear_acceleration_buf[WINDOW_SIZE].clear();angular_velocity_buf[WINDOW_SIZE].clear();
//            ROS_DEBUG("marg_flag: %d, before marg, all_image_frame.size(): %lu, WINDOW_SIZE: %d",
//                      marginalization_flag, all_image_frame.size(), WINDOW_SIZE);if (true || solver_flag == INITIAL){map<double, ImageFrame>::iterator it_0;it_0 = all_image_frame.find(t_0);//t_0是最老幀的時間戳，marg_old時刪掉了幀，但是marg2nd的時候沒有動，但是在process時候加進來了，說明all_image_frame應該是在增長的delete it_0->second.pre_integration;it_0->second.pre_integration = nullptr;for (map<double, ImageFrame>::iterator it = all_image_frame.begin(); it != it_0; ++it){if (it->second.pre_integration)delete it->second.pre_integration;it->second.pre_integration = NULL;}all_image_frame.erase(all_image_frame.begin(), it_0);//erase掉從開始到被marg掉的old之間所有的幀[begin(), it_0)all_image_frame.erase(t_0);//erase掉old幀}slideWindowOld();//求prior，刪除某些變量
//            ROS_DEBUG("marg_flag: %d, after marg, all_image_frame.size(): %lu, WINDOW_SIZE: %d",
//                      marginalization_flag, all_image_frame.size(), WINDOW_SIZE);}}//如果2nd不是KF則直接扔掉1st的visual測量，并在2nd基礎上對1st的IMU進行預積分，window前面的都不動else{if (frame_count == WINDOW_SIZE){
//            ROS_DEBUG("marg_flag: %d, before marg, all_image_frame.size(): %lu, WINDOW_SIZE: %d",
//                      marginalization_flag, all_image_frame.size(), WINDOW_SIZE);for (unsigned int i = 0; i < dt_buf[frame_count].size(); i++)//對最新幀的img對應的imu數據進行循環{double tmp_dt = dt_buf[frame_count][i];Vector3d tmp_linear_acceleration = linear_acceleration_buf[frame_count][i];Vector3d tmp_angular_velocity = angular_velocity_buf[frame_count][i];pre_integrations[frame_count - 1]->push_back(tmp_dt, tmp_linear_acceleration, tmp_angular_velocity);//2nd對1st進行IMU預積分//imu數據保存，相當于一個較長的KF，eg：//     |-|-|-|-|-----|//                ↑//            這段img為1st時，2nd不是KF，扔掉了這個1st的img，但buf了IMU數據，所以這段imu數據較長dt_buf[frame_count - 1].push_back(tmp_dt);linear_acceleration_buf[frame_count - 1].push_back(tmp_linear_acceleration);angular_velocity_buf[frame_count - 1].push_back(tmp_angular_velocity);}//相對世界系的預積分需要繼承過來Headers[frame_count - 1] = Headers[frame_count];Ps[frame_count - 1] = Ps[frame_count];Vs[frame_count - 1] = Vs[frame_count];Rs[frame_count - 1] = Rs[frame_count];Bas[frame_count - 1] = Bas[frame_count];Bgs[frame_count - 1] = Bgs[frame_count];delete pre_integrations[WINDOW_SIZE];pre_integrations[WINDOW_SIZE] = new IntegrationBase{acc_0, gyr_0, Bas[WINDOW_SIZE], Bgs[WINDOW_SIZE]};dt_buf[WINDOW_SIZE].clear();linear_acceleration_buf[WINDOW_SIZE].clear();angular_velocity_buf[WINDOW_SIZE].clear();slideWindowNew();
//            ROS_DEBUG("marg_flag: %d, after marg, all_image_frame.size(): %lu, WINDOW_SIZE: %d",
//                      marginalization_flag, all_image_frame.size(), WINDOW_SIZE);}}
}

7.2 slideWindowOld(理解marg視覺觀測、三角化、綁定深度)

其中，在marg_old時VINS-MONO并未在每次marg時刪除第[0]幀看到的所有landmark，當該feature只被[0]觀測到時才會刪除該feature，有些博客沒有說清楚，會產生誤解。

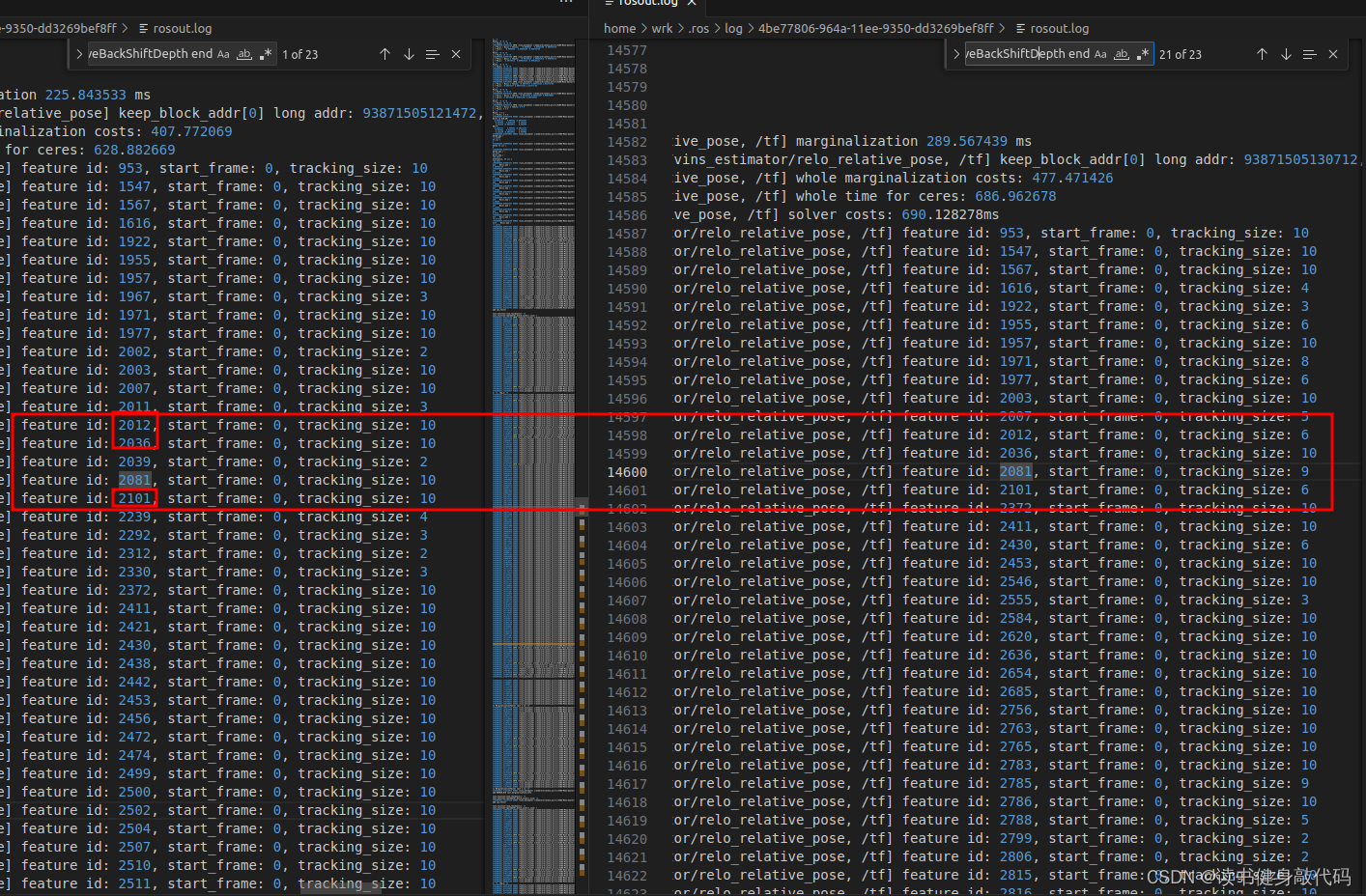
下圖可見在第1次和第21次removeBackShiftDepth結束時仍有之前tracking到的feature

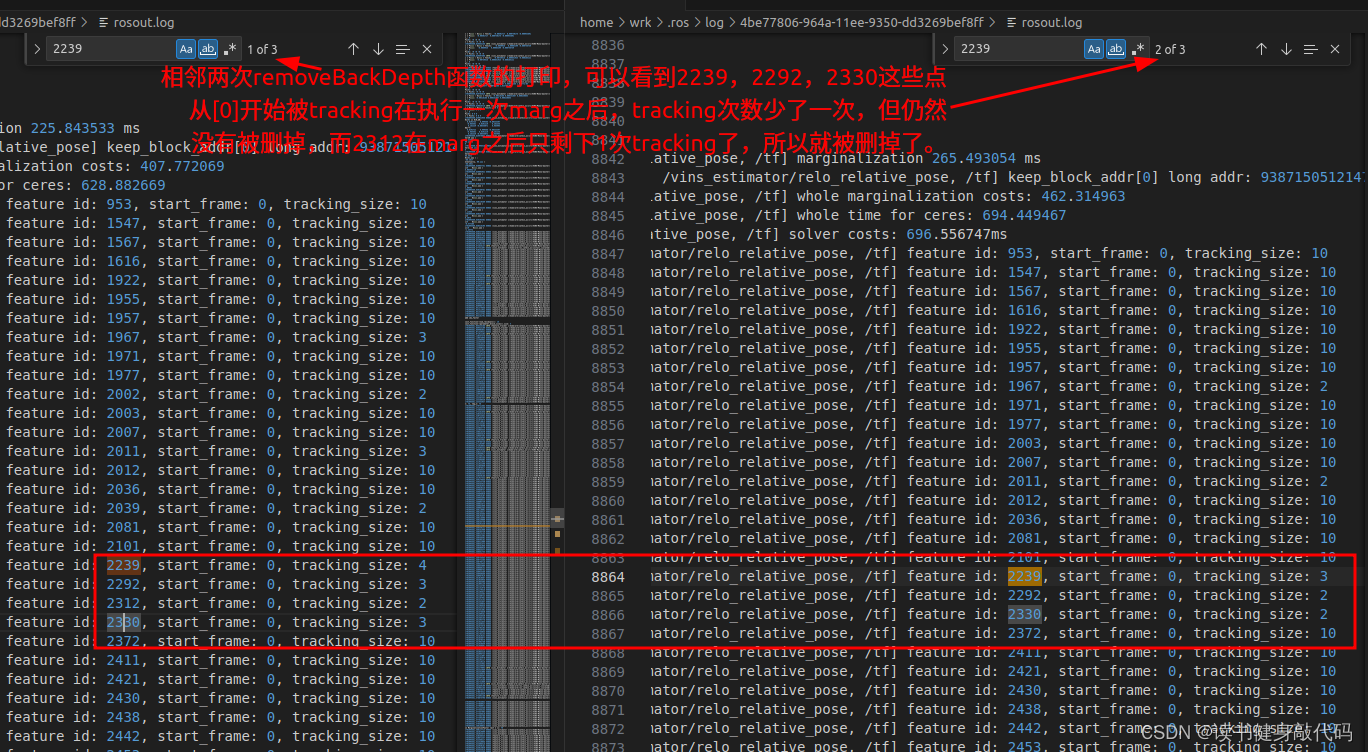
下圖表明VINS-MONO并未刪除始于第[0]幀看到的所有landmark，僅僅是當只在[0]有一次tracking時才會刪除：

除了刪除[0]的觀測，還應該處理[0]作為start_frame該幀對應的camera系上綁定的深度，將其傳遞到后面的幀中，此部分解釋見上一篇博客的2.4.3.1節。

degbu代碼：

//由于三角化出的camera系下的深度都綁定在start_frame上，所以當marg掉start_frame時，要將深度傳遞給后面的幀，這里綁定在了start_frame下一幀
void FeatureManager::removeBackShiftDepth(Eigen::Matrix3d marg_R, Eigen::Vector3d marg_P, Eigen::Matrix3d new_R, Eigen::Vector3d new_P)
{for (auto it = feature.begin(), it_next = feature.begin();it != feature.end(); it = it_next){it_next++;//不始于第[0]幀的landmark的start_frame前移，//始于第[0]幀的landmark，1.如果只在[0]tracking，則直接刪掉（因為僅1幀算不出深度），2.如果tracking多于1幀，則將深度傳遞給start_frame+1幀//管理marg之后的start_frame，要往前移1if (it->start_frame != 0)it->start_frame--;else{Eigen::Vector3d uv_i = it->feature_per_frame[0].point;  it->feature_per_frame.erase(it->feature_per_frame.begin());if (it->feature_per_frame.size() < 2){feature.erase(it);continue;}else{Eigen::Vector3d pts_i = uv_i * it->estimated_depth;//歸一化->camera_margEigen::Vector3d w_pts_i = marg_R * pts_i + marg_P;//Twc_marg * camera = worldEigen::Vector3d pts_j = new_R.transpose() * (w_pts_i - new_P);//Twc_new^(-1) * world=camera_newdouble dep_j = pts_j(2);if (dep_j > 0)it->estimated_depth = dep_j;elseit->estimated_depth = INIT_DEPTH;}ROS_DEBUG("feature id: %d, start_frame: %d, tracking_size: %lu",it->feature_id, it->start_frame, it->feature_per_frame.size());}// remove tracking-lost feature after marginalize/*if (it->endFrame() < WINDOW_SIZE - 1){feature.erase(it);}*/}ROS_DEBUG("this removeBackShiftDepth end");
}

7.3 slideWindowNew

這部分屬于MARGIN_SECOND_NEW的內容，MARGIN_SECOND_NEW中只marg掉了此時先驗中關于2nd的視覺pose，連2nd對landmark的觀測都沒有向后傳遞info，這部分觀測在slideWindow()中直接丟掉了。

optimization()中關于MARGIN_SECOND_NEW部分挑選drop_set的部分，只filter出了2nd的pose，沒有視覺的factor：

//只drop掉2nd的視覺pose（IMU部分是在slideWindow內繼承和delete的）
vector<int> drop_set;
for (int i = 0; i < static_cast<int>(last_marginalization_parameter_blocks.size()); i++)
{ROS_ASSERT(last_marginalization_parameter_blocks[i] != para_SpeedBias[WINDOW_SIZE - 1]);if (last_marginalization_parameter_blocks[i] == para_Pose[WINDOW_SIZE - 1])drop_set.push_back(i);
}

在slideWindow()中直接丟掉了，而這樣做的理論依據是認為2nd和1st非常相似，所以對IMU直接繼承預積分，對視覺pose直接丟棄，以下是崔華坤的解釋：

8. 總結

本文主要講解了VINS-MONO中的marginalization，marg的目的是為了維護我們優化問題的復雜度在一定的范圍內，在新變量進來之前要把舊變量剔除出去，同時要保留舊變量對剩余變量的約束信息。

VINS-MONO有兩種marg策略，

• 2nd為KF，則marg old
• 2nd非KF，則marg 2nd的pose，并繼承IMU積分

保留marg變量的核心方法是Schur Compliment，原理方面，涉及到了

• marg landmark的理解（marglandmark觀測而非直接marg整個路標點）
• 先驗誤差$e_p$的更新
• 先驗Jacobian不變帶來的問題
• 魯棒核函數如何對residual和Jacobian使用
• 三角化輸出深度的理解（綁定在start_frame上）
• 整個系統Jacobian和information mattix理解

編程方面，涉及到了

• map地址映射
• 內存管理
• 多線程
• 提高double類型矩陣的數值穩定性
• SVD分解加速矩陣求逆過程(GPT真香)

水平有限，如有紕漏，歡迎指正。

接下來是pose_graph部分。