?
🌈個人主頁:?Aileen_0v0
🔥系列專欄:?數據結構與算法
💫個人格言:"沒有羅馬,那就自己創造羅馬~"
這篇博客主要探索的是計算機科學常見問題---搜索算法
“時間緊，任務重！”
話不多說，開始今天的學習之旅吧?~
目錄
搜索
定義
關鍵字-in
順序搜索?
無序表的順序搜索過程
無序表的順序搜索代碼實現?
分析順序搜索算法
有序列表
有序列表的順序搜索過程?編輯
無序表的順序搜索代碼實現?
搜索
定義
搜索是指從元素集合中找到特定元素的算法過程。
搜索過程通常返回True 或 False 來表示元素是否在集合中。
有時也可以修改搜索過程，使它返回目標元素的位置。
為了更好的打好算法基礎，我們這次先探索搜索的元素是否存在這一問題。
關鍵字-in
in是Python中的關鍵字，用于判斷一個元素是否存在于一個容器中。可以用于列表、元組、字典、集合等數據類型。它可以被用于for循環語句 和 if語句中。
我們之前做Python每日一練時我曾科普過Python中 我們可以通過運算符 —— in 去檢查元素是否在列表中。
print(15 in [1,2,3])
print(15 in [1,2,3,15])運行結果：?
順序搜索?
線性結構（數組、鏈表、棧、隊列等）都有下標。每個數據項都有一個相對于其它數據項的位置。
Python的列表 ，數據項的位置就是其下標。
因為下標是有序的，So 我們能夠進行 順序訪問 及 順序搜索。
無序表的順序搜索過程
下圖展示了順序搜索的過程。
無序表的順序搜索代碼實現?
def sequential_search(a_list,item):pos = 0while pos < len(a_list):if a_list[pos] == item:return Truepos += 1return Falseprint(sequential_search([1,2,4,5,9],5))從列表第一個元素開始， 沿著下表順序逐個查看，直到找到目標元素或者到達列表末尾。
若查完列表后仍未找到目標元素，則說明目標元素不在列表中。
分析順序搜索算法
分析搜索算法前，首先需要先定義 計算的基本單元---解決問題過程中不斷重復的的某一步。
對搜索來說，記錄 比較的次數 是合理的 性能指標。
每次比較只有兩個結果： 找到目標元素，或未找到。
假設元素排列無序，則目標元素在每一個位置出現的可能都相同。
要確定目標元素是否在列表中，唯一的方法就是將它與列表中的每個元素都比較一次。
若列表中有n個元素，那么順序搜索要經過 n 次比較后才能確定目標元素不在列表中。如果列表含目標元素，分析起來更復雜。實際上有 3 種可能的情況：
最好情況是目標元素位于列表的第一個位置，則只需比較一次;
最壞情況是目標元素位于最后一個位置，則需要比較 n次。
平均情況是目標元素位于中間位置，則需要比較 n / 2次。 --> 當n增大，系數則可省略，所以順序搜索時間復雜度為O（n）。
有序列表
有序列表的順序搜索過程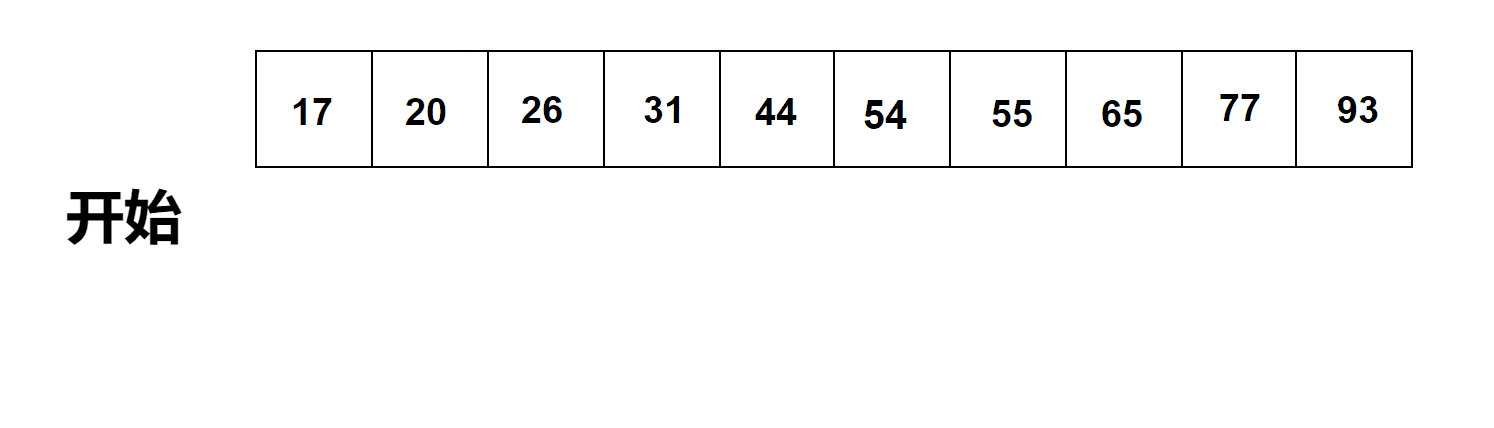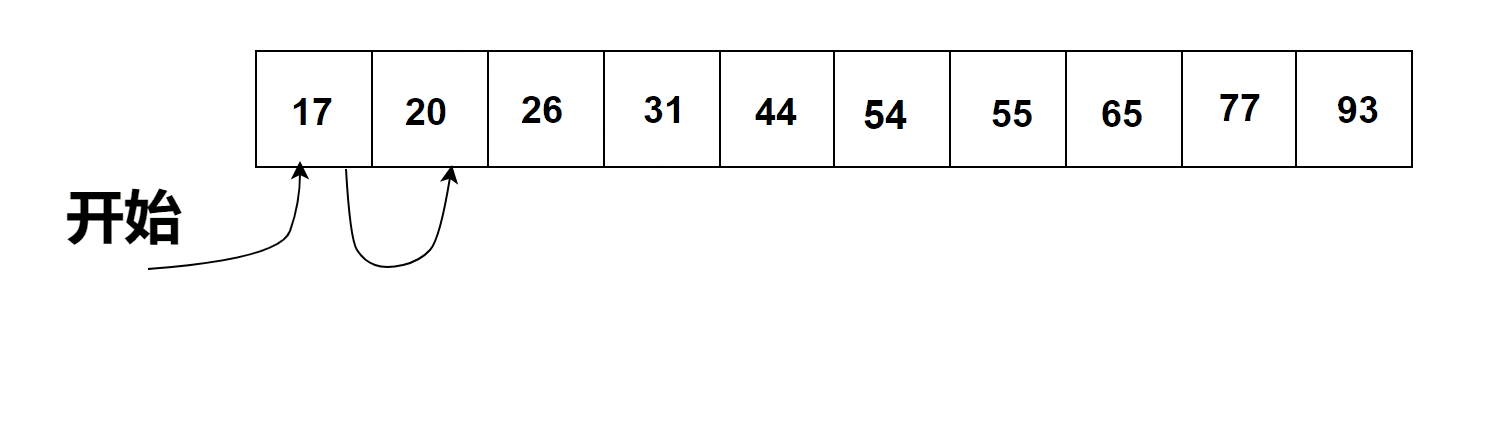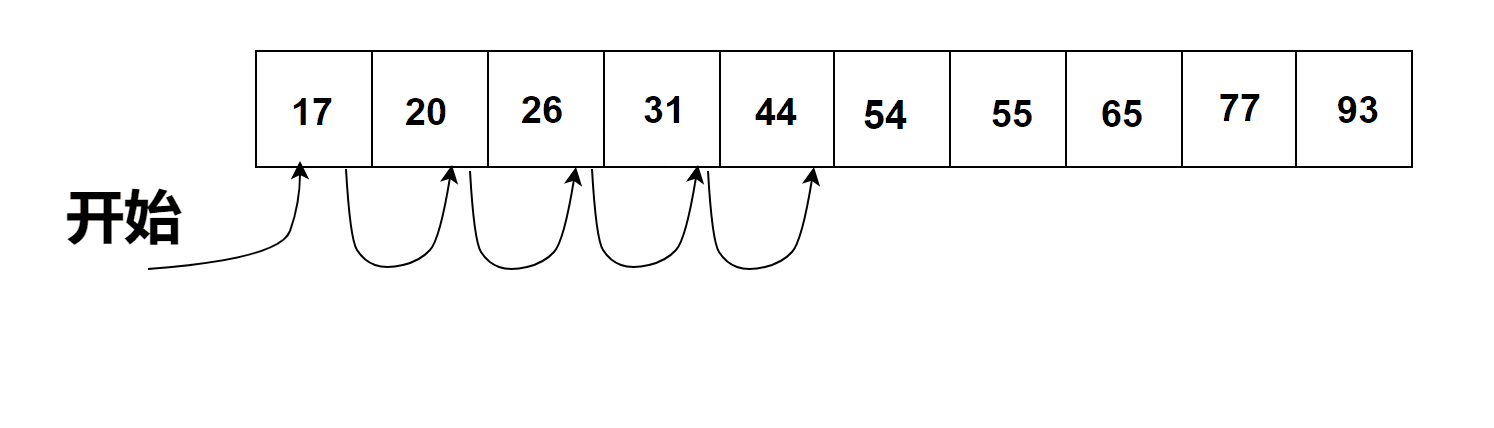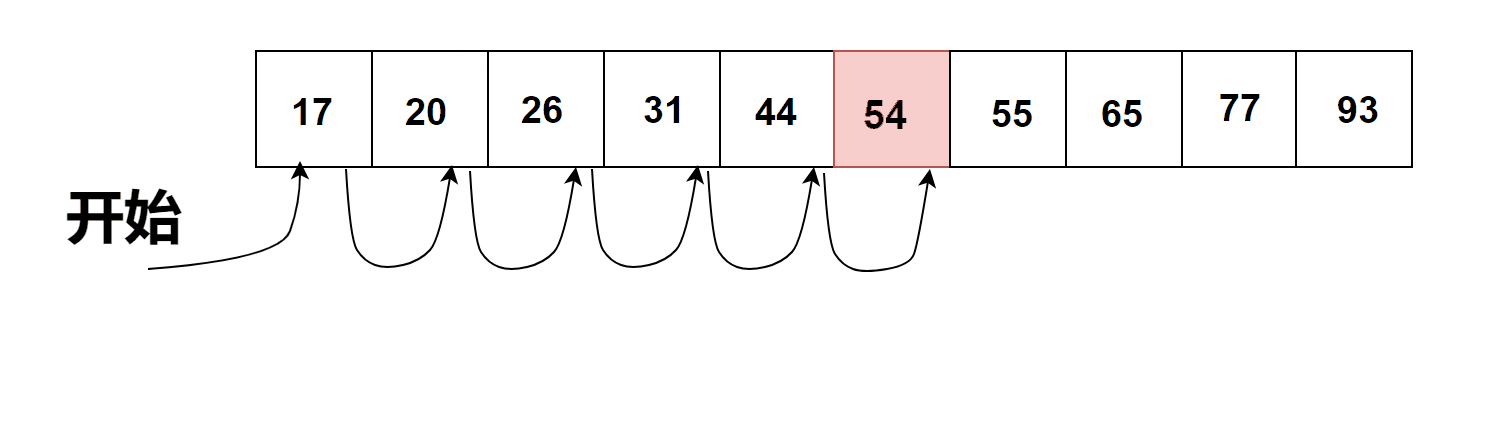
通過觀察上圖有序列表列表中的順序搜索過程我們可以得出以下結論：
當元素按升序排列。
如果存在目標元素，那么它出現在 n個位置中任意一個位置的可能性仍然一樣大，因此比較次數與在無序列表中相同。
But，如果不存在目標元素，那么搜索效率就會提高。---> 因為當找到比目標元素大的數的時候程序就會停止搜索。
無序表的順序搜索代碼實現?
#有序表的順序搜索
def ordered_sequential_search(a_list,item):pos = 0while pos < len(a_list):if a_list[pos] == item:return Trueelif a_list[pos] > item:return Falsepos += 1return False
print(ordered_sequential_search([1,2,4,5,9],6))下表總結了，在有序表中搜索時的比較次數。
最好情況：只需比較1次。? 平均情況：比較 n / 2 次，但時間復雜度仍是O（n）。
總結：只有當列表不存在目標元素時，有序排列的元素，才能提高順序搜索的效率。
📝總結：
本篇文章介紹了搜索算法以及，有序列表在搜索算法中 的優勢，前提條件是：只有當元素不在列表中時，有序排列的元素，才能提高順序搜索的效率。
--目錄)
