一、五種算法(SWO、COA、LSO、GRO、LO)簡介
1、蜘蛛蜂優化算法SWO
蜘蛛蜂優化算法(Spider?wasp optimizer,SWO)由Mohamed Abdel-Basset等人于2023年提出,該算法模型雌性蜘蛛蜂的狩獵、筑巢和交配行為,具有搜索速度快,求解精度高的優勢。VRPTW(MATLAB):蜘蛛蜂優化算法SWO求解帶時間窗的車輛路徑問題VRPTW(提供參考文獻及MATLAB代碼)-CSDN博客
參考文獻:
[1]Abdel-Basset, M., Mohamed, R., Jameel, M. et al. Spider wasp optimizer: a novel meta-heuristic optimization algorithm. Artif Intell Rev (2023). Spider wasp optimizer: a novel meta-heuristic optimization algorithm | SpringerLink
2、小龍蝦優化算法COA
小龍蝦優化算法(Crayfsh optimization algorithm,COA)由Jia Heming?等人于2023年提出,該算法模擬小龍蝦的避暑、競爭和覓食行為,具有搜索速度快,搜索能力強,能夠有效平衡全局搜索和局部搜索的能力。多目標優化算法:基于非支配排序的小龍蝦優化算法(NSCOA)MATLAB-CSDN博客
參考文獻:
[1] Jia, H., Rao, H., Wen, C. et al. Crayfish optimization algorithm. Artif Intell Rev (2023). Crayfish optimization algorithm | SpringerLink
3、光譜優化算法LSO
光譜優化算法(Light Spectrum Optimizer,LSO)由Mohamed Abdel-Basset等人于2022年提出。MD-MTSP:光譜優化算法LSO求解多倉庫多旅行商問題MATLAB(可更改數據集,旅行商的數量和起點)-CSDN博客
參考文獻:
[1]Abdel-Basset M, Mohamed R, Sallam KM, Chakrabortty RK. Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm. Mathematics. 2022; 10(19):3466. Mathematics | Free Full-Text | Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm
4、淘金優化算法GRO
淘金優化算法(Gold rush optimizer,GRO)由Kamran Zolf于2023年提出,其靈感來自淘金熱,模擬淘金者進行黃金勘探行為。VRPTW(MATLAB):淘金優化算法GRO求解帶時間窗的車輛路徑問題VRPTW(提供參考文獻及MATLAB代碼)-CSDN博客
參考文獻:
K. Zolfi. Gold rush optimizer: A new population-based metaheuristic algorithm. Operations Research and Decisions 2023: 33(1), 113-150. DOI 10.37190/ord230108
5、狐猴優化算法
狐猴優化算法(Lemurs Optimizer,LO)由Ammar Kamal Abasi等人于2022年提出,該算法模擬狐猴的跳躍和跳舞行為,具有結構簡單,思路新穎,搜索速度快等優勢。單目標應用:基于狐猴優化算法(Lemurs Optimizer,LO)的微電網優化調度MATLAB-CSDN博客
參考文獻:
[1]Abasi AK, Makhadmeh SN, Al-Betar MA, Alomari OA, Awadallah MA, Alyasseri ZAA, Doush IA, Elnagar A, Alkhammash EH, Hadjouni M. Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization. Applied Sciences. 2022; 12(19):10057. Applied Sciences | Free Full-Text | Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization
二、模型簡介
單個無人機三維路徑規劃問題及其建模_IT猿手的博客-CSDN博客
參考文獻:
[1]胡觀凱,鐘建華,李永正,黎萬洪.基于IPSO-GA算法的無人機三維路徑規劃[J].現代電子技術,2023,46(07):115-120
三、SWO、COA、LSO、GRO、LO求解無人機路徑規劃
(1)部分代碼
close all
clear??
clc
warning off;
%% 三維路徑規劃模型定義
global startPos goalPos N
N=2;%待優化點的個數(可以修改)
startPos = [10, 10, 80]; %起點(可以修改)
goalPos = [80, 90, 150]; %終點(可以修改)
SearchAgents_no=30; % 種群大小(可以修改)
Function_name='F1'; %F1:隨機產生地圖 F2:導入固定地圖
Max_iteration=100; %最大迭代次數(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
AlgorithmName={'SWO','COA','LSO','GRO','LO'};%算法名稱
addpath('./AlgorithmCode/')%添加算法路徑
bestFit=[];%保存各算法的最優適應度值
for i=1:size(AlgorithmName,2)%遍歷每個算法,依次求解當前問題
Algorithm=str2func(AlgorithmName{i});%獲取當前算法名稱,并將字符轉換為函數
[Best_score,Best_pos,Convergence_curve]=Algorithm(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%當前算法求解
%將當前算法求解結果放入data中
data(i).Best_score=Best_score;%保存該算法的Best_score到data
data(i).Best_pos=Best_pos;%保存該算法的Best_pos到data
data(i).Convergence_curve=Convergence_curve;%保存該算法的Convergence_curve到data
bestFit=[bestFit data(i).Best_score];
end
save data data
%%? 畫各算法的直方圖
figure?
bar(bestFit)
ylabel('無人機飛行路徑長度');
set(gca,'xtick',1:1:size(AlgorithmName,2));
set(gca,'XTickLabel',AlgorithmName)
saveas(gcf,'./Picture/直方圖.jpg') %將圖片保存到Picture文件夾下面%%? 畫收斂曲線
strColor={'r--','g-','b-.','k--','m:','c-','y-'};
figure
for i=1:size(data,2)
plot(data(i).Convergence_curve,strColor{i},'linewidth',1.5)%semilogy
hold on
end
xlabel('迭代次數');
ylabel('無人機飛行路徑長度');
legend(AlgorithmName,'Location','Best')
saveas(gcf,'./Picture/收斂曲線.jpg') %將圖片保存到Picture文件夾下面%% 顯示三維圖并保存
path=plotFigure(data,AlgorithmName,strColor);%path是各算法求解的無人機路徑
saveas(gcf,'./Picture/路徑曲線(三維).jpg') %將圖片保存到Picture文件夾下面
save path path
%% 顯示二維圖并保存
view(2)
saveas(gcf,'./Picture/路徑曲線(二維).jpg') %將圖片保存到Picture文件夾下面%% 顯示三維圖
path=plotFigure(data,AlgorithmName,strColor);%三維圖 path是各算法求解的無人機路徑
(2)部分結果
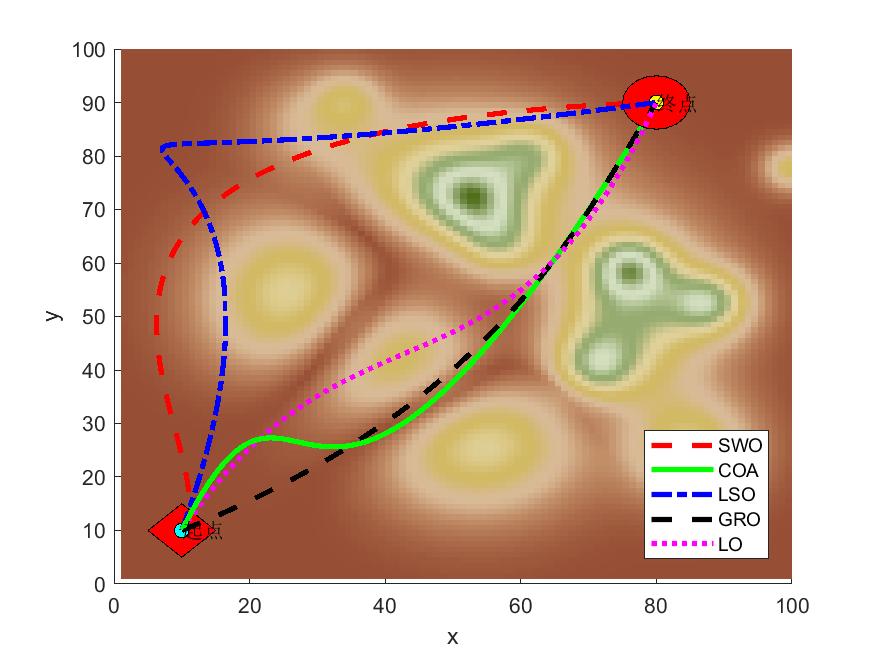


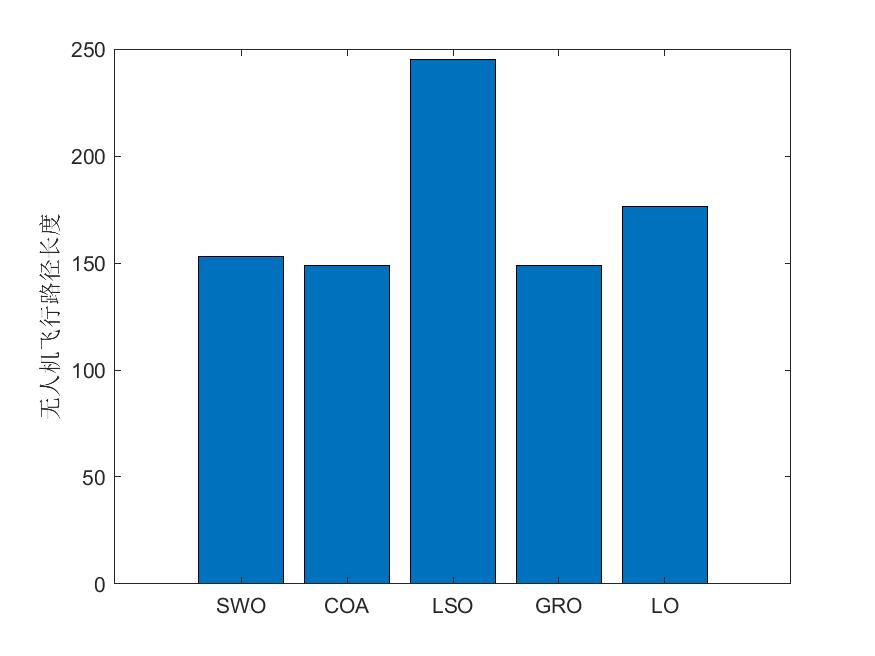
四、完整MATLAB代碼







)
)






)

| AgentTuning:清華大學與智譜AI提出AgentTuning提高大語言模型Agent能力)
)
