139. 單詞拆分 - 力扣(LeetCode)
給你一個字符串?s?和一個字符串列表?wordDict?作為字典。請你判斷是否可以利用字典中出現的單詞拼接出?s?。
注意:不要求字典中出現的單詞全部都使用,并且字典中的單詞可以重復使用。
示例 1:
輸入: s = "leetcode", wordDict = ["leet", "code"] 輸出: true 解釋: 返回 true 因為 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
輸入: s = "applepenapple", wordDict = ["apple", "pen"] 輸出: true 解釋: 返回 true 因為 "applepenapple"可以由 "apple" "pen" "apple" 拼接成。注意,你可以重復使用字典中的單詞。
思路:完全背包問題,單詞就是物品,字符串s就是背包,單詞能否組成字符串s,就是問物品能不能把背包裝滿。轉換成背包問題有兩個難點:①dp[i]是如何來的,②遍歷順序。
解決:動態規劃五步曲
? ? ? ? 1.確定dp[j]的含義;
????????dp[i] : 字符串長度為i的話,dp[i]為true,表示可以拆分為一個或多個在字典中出現的單詞。
? ? ? ? 2.確定dp[j]遞推公式;
? ? ? ? 這里遞推公式好像和之前不同,這里既沒有01背包的價值,又沒有完全背包的組合數量,通過dp[j]的含義我們知道,dp[i]要不就是true,要不就是false,我們要的就是true。
? ? ? ??如果確定dp[j] 是true,且 [j, i] 這個區間的子串出現在字典里,那么dp[i]一定是true。(j < i )。所以遞推公式是 if([j, i] 這個區間的子串出現在字典里 && dp[j]是true) 那么 dp[i] = true。
? ? ? ? 到這里有點懵了,i是字符串長度,那j是什么,j這里其實表示當前遍歷字符串中的位置。
? ? ? ? 舉個例子:s = "leet", wordDict = ["le", "et"]
? ? ? ? i等于1時,j就從0開始,j=0時,截取i-j就是le,發現wordDict中有“le”,所以dp[i]=true。
? ? ? ? 3.確定dp初始化;
? ? ? ? 沒開始前,dp[i]=false,但是從遞推公式中可以看出,dp[i] 的狀態依靠 dp[j]是否為true,那么dp[0]就是遞推的根基,dp[0]一定要為true,否則遞推下去后面都都是false了
? ? ? ? 4.確定遍歷順序;
? ? ? ? 從上面分析可知,隨著字符串長度i增大,依次遍歷,能在wordDict中找到的單詞肯定越多,結果也越有可能是true。,所以本題一定是先遍歷背包,再遍歷物品。
? ? ? ? 舉個例子:拿 s = "applepenapple", wordDict = ["apple", "pen"] 舉例。
????????"apple", "pen" 是物品,那么我們要求 物品的組合一定是 "apple" + "pen" + "apple" 才能組成 "applepenapple"。"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的,那么我們就是強調物品之間順序。
? ? ? ? 5.舉例推導dp數組。
????????以輸入: s = "leetcode", wordDict = ["leet", "code"]為例,dp狀態如圖:
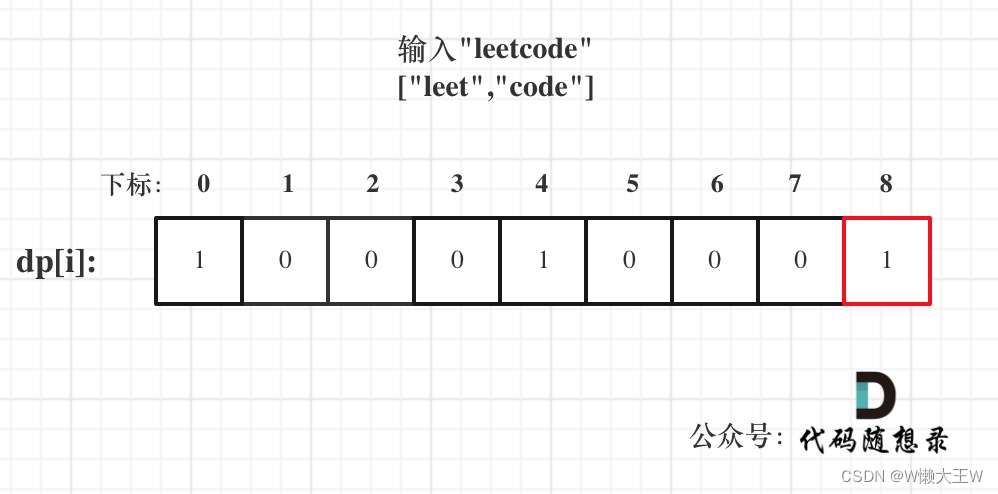
代碼:這里利用unordered_set判斷是否在wordDict中找到單詞。
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {vector<bool> dp(s.size()+1,false);unordered_set<string> wordSet(wordDict.begin(), wordDict.end());dp[0]=true;for(int i=0;i<=s.size();i++){for(int j=0;j<i;j++){string word = s.substr(j, i - j); //substr(起始位置,截取的個數)if(wordSet.find(word) != wordSet.end()&&dp[j]){//dp[j]表示前j個長度的字符串可以由單詞拼接,并且截取的子字符串在數組中dp[i]=true;}}}return dp[s.size()];}
};多重背包
????????例題:有N種物品和一個容量為V 的背包。第i種物品最多有Mi件可用,每件耗費的空間是Ci ,價值是Wi 。求解將哪些物品裝入背包可使這些物品的耗費的空間 總和不超過背包容量,且價值總和最大。
????????區別:多重背包和01背包是非常像的,每件物品最多有Mi件可用,把Mi件攤開,其實就是一個01背包問題了。
????????面試基本不會考,了解即可。
背包問題總結
難點:遞推公式和遍歷順序
步驟:
- 確定dp數組(dp table)以及下標的含義
- 確定遞推公式
- dp數組如何初始化
- 確定遍歷順序
- 舉例推導dp數組
遞推公式總結:
? ? ? ? 1.問能否能裝滿背包(或者最多裝多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
? ? ? ? 2.?問裝滿背包有幾種方法:dp[j] += dp[j - nums[i]]?
? ? ? ? 3.問背包裝滿最大價值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
? ? ? ? 4.問裝滿背包所有物品的最小個數:dp[j] = min(dp[j - coins[i]] + 1, dp[j])
遍歷順序總結:
? ? ? ? 1.01背包
? ? ? ? ①二維數組:二維dp數組01背包先遍歷物品還是先遍歷背包都是可以的,且第二層for循環是從小到大遍歷。
? ? ? ? ②一維數組:一維dp數組01背包只能先遍歷物品再遍歷背包容量,且第二層for循環是從大到小遍歷。
? ? ? ? 2.完全背包
? ? ? ? ①如果求組合數就是外層for循環遍歷物品,內層for循環遍歷背包。
? ? ? ? ②如果求排列數就是外層for循環遍歷背包,內層for循環遍歷物品。
總結:對于背包問題,其實遞推公式算是容易的,難是難在遍歷順序上,如果把遍歷順序搞透,才算是真正理解了。
)










)

基本語法)





