上一篇

人工智能原理復習–搜索策略（一）

啟發式搜索

提高一般圖搜索效率的關鍵是優化OPEN表中節點的排序方式
最理想的情況是每次排序OPEN表表首n總在解答路徑上

全局排序–對OPEN表中的所有節點進行排序（A算法，A*算法）
局部排序–僅對新擴展出來的子節點排序（爬山法）

A算法
基本思想：
設計體現啟發式知識的評價函數 $f(n)$指導OPEN表中帶擴展節點的排序。
評價函數：$f(n)=g(n)+h(n)$
n – 搜索圖G中的節點
f(n) – G中從初始狀態節點s，經由節點n到達目標節點$n_g$, 估計的最小代價
g(n) – G中從s到n，目前實際的路徑代價
h(n) – 從n到$n_g$, 估計的最小代價
h(n)稱為啟發式函數

與一般圖搜索順序類似
但是在擴展n的節點時對每個子節點 $n_i$計算$f(n,n_i)=g(n,n_i)+h(n_i)$
然后適當標記修改指針，排序OPEN表

實現啟發式搜索應考慮的關鍵因素：

1. 搜索算法的可采納性
2. 啟發式函數h(n)的強弱及其影響

若一個搜索算法總能找到最短（代價最小）的解答路徑，則稱該狀態空間的搜索算法具有可采納性，也叫最優性。
寬度優先搜索算法是可采納的，只是搜索效率不高。
A算法是可采納的



.
$A^{?}算法$
如果A算法是可采納的則$f^{?}(n)=g^{?}(n)+h^{?}(n)$
*代表實際的最短路徑
理想情況下：$g(n)=g^{?}(n)、h(n)=h^{?}(n)$
每次搜索過程中不擴展任何無關結點

而實際情況下g(n)容易在已經生成搜索樹中計算出來，但是h(n)具有未知性，只能盡可能靠近$h^{?}(n)$

因此可以得出$A^{?}算法定義$：
在A算法中，規定$h(n)<=h^{?}(n)$
A算法中最優秀的就是$A^{?}$算法

而 h(n)接近$h^{?}(n)$的程度–是衡量啟發式函數的強弱

• $h(n)<h^{?}(n)$且差距過大，排序誤差較大，產生更大的搜索圖，無用節點更多
• $h(n)>h^{?}(n)$且h(n)過強，A算法失去可采納性，不能確保找到最短路徑
• $h(n)=h^{?}(n)$可以確保生成最小的搜素圖，找到最短路徑

因此$A^{?}$算法就是在$h(n)<=h^{?}(n)$的條件下，越大越好。

若h(n) = 0 $?$ BFS
若g(n) = 0 $?$ DFS

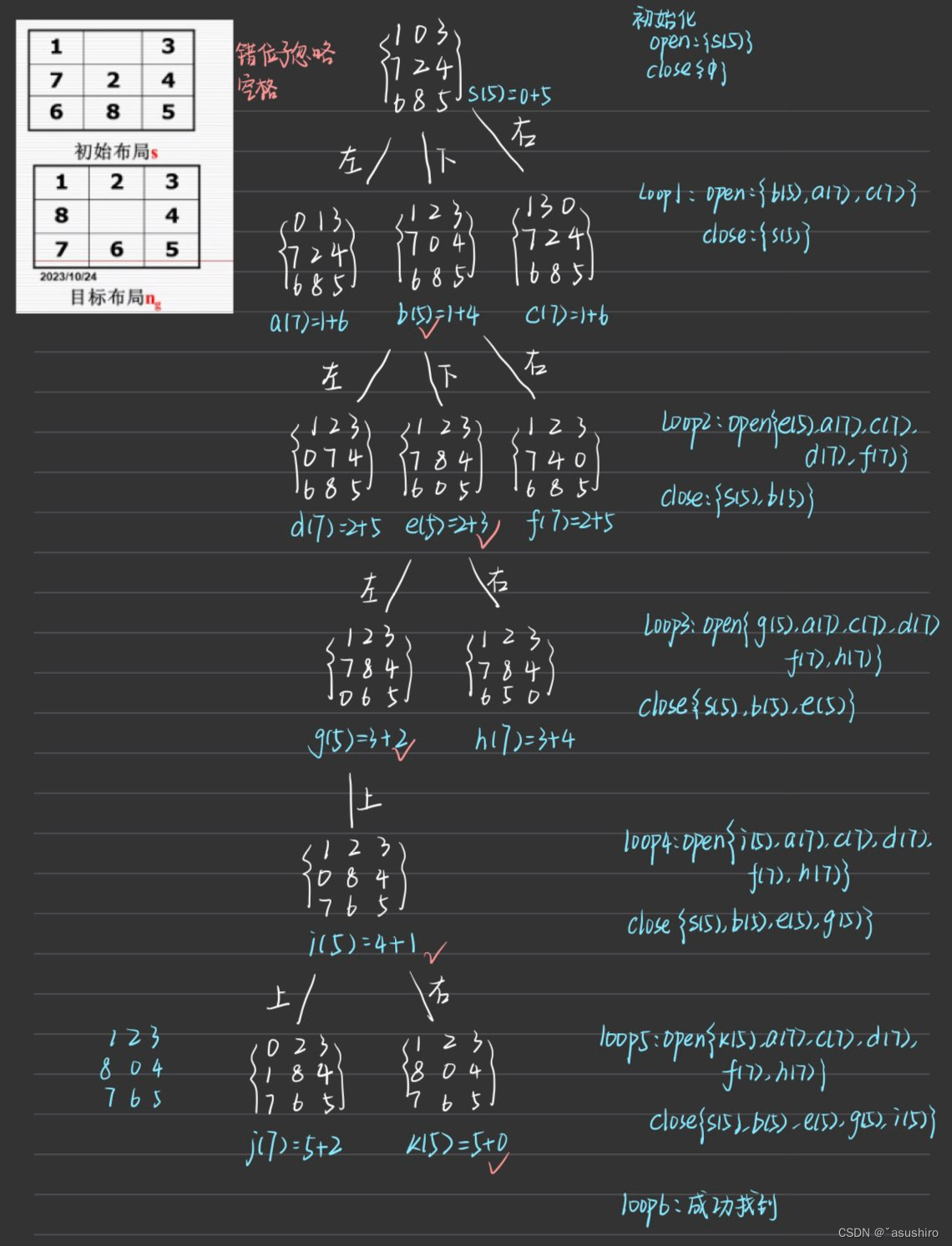
通過模擬過程，和算法設計與分析的堆優化的分支界限法相似

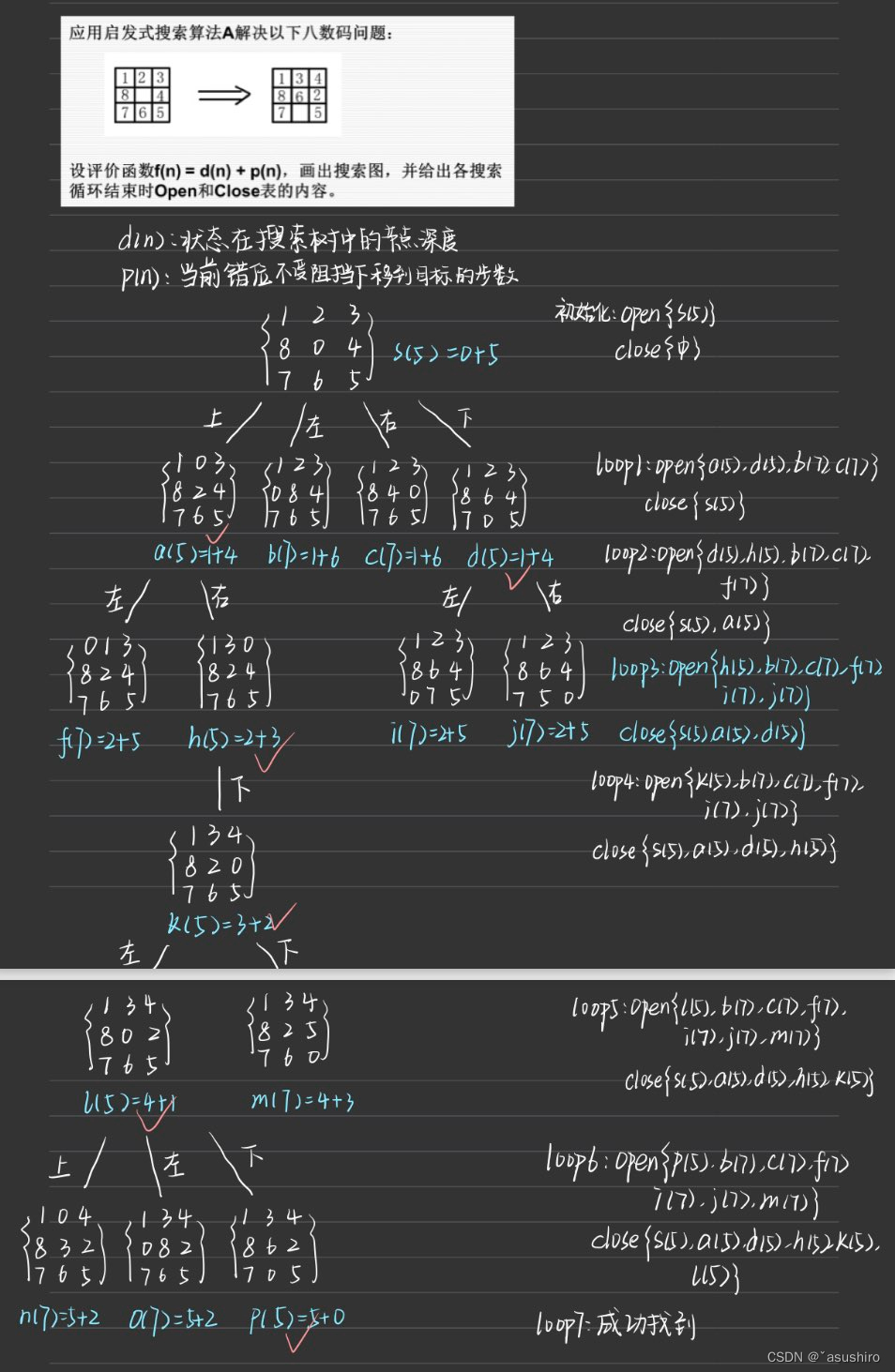
close表就是已經訪問過的狀態，open表就是待訪問的狀態，而評估函數就是找出下一個最先訪問的狀態

定義狀態空間，
定義對應狀態的h(n)


為更有效地搜索解答，可使用評價函數$f(n)=g(n)+w?h(n)$,添加一個加權
在搜索圖的淺層（上部），可讓w取較大值，使得搜索加速向縱深方向搜索
當搜索到較深的層次時，再讓 $w$ 取較小值， 保證$wh(n)<=h^{?}(n)$的情況下，在橫向方向發展，尋找較短的解答路徑

迭代加深$A^{?}$算法
由于$A^{?}$算法會將節點全部保存在內存中，所以$A^{?}$算法困在空間問題
因此有了迭代加深$A^{?}$算法 $ID{A}^{?}$算法
但是不滿足最優性和完備性
它以深度優先的方式在有限制的深度內搜索目標節點，在每個深度上，該算法在每個深度上都會檢查節點是否出現如果出現則停止，否則深度加一繼續搜索。啟發函數用作深度的限制, 而不是選擇擴展結點的排序。

特點：由于$A^{?}$算法需要指數級的存儲空間，沒有深度限制，而$ID{A}^{?}$算法可以節省大量內存。當啟發式函數是最優的時候，$ID{A}^{?}$算法和$A^{?}$算法擴展相同的結點，并且可以找到最優路徑。

與或圖搜索

問題歸約：是將復雜問題轉換成若干需要同時處理的較為簡單的子問題后再加以分別求解，只有子問題全部解決時，問題才算解決。問題的解答由子問題的解答聯合構成。
實質就是，將目標逆向推理分解成一個個子問題，直至最后把初始問題歸約為一個平凡的本原問題集合。

運用問題歸約策略得到的狀態空間圖稱為與或圖。

表示：
用圓弧將幾條節點間關聯弧連接起來，子問題全部解決才能導致原問題解決。
或關系$\to$解決其中一個或關系就能解決上層問題

與或圖基本概念：

• K-連接：父節點與K個子節點連接，子節點之間是與關系。
  一個父節點可以有多個K-連接（與關系）
  K-連接之間是或關系
• 解圖：解答路徑不復存在，取而代之的是廣義的接路徑----解圖, 解圖是純粹的與圖，節點之間不存在或關系。
• 終節點：能用于聯合表示目標狀態的節點

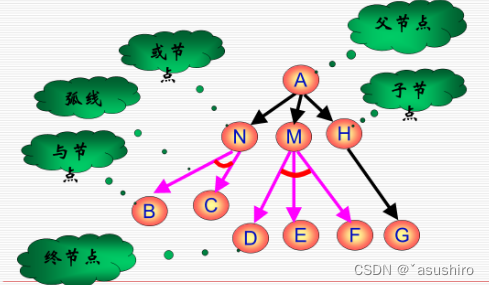
• 解圖的生成：從根節點選K-連接，然后從子節點再選擇K-連接直到所有K-節點都指向終節點為止。存在或關系可能搜索到多個解圖。

• 解圖的代價：
  令K-連接的代價就是K
  則代價$C(n)=K+C(n_1)+C(n_2)+...+C(n_k)$

• 能解節點：
  終節點是能解節點，若K-連接的子節點都是能解節點則這個父節點也是能解節點。

• 不能解節點：
  非終節點是不能解節點，若K-連接至少連接一個不能解節點則父節點是不能解節點

AO*算法

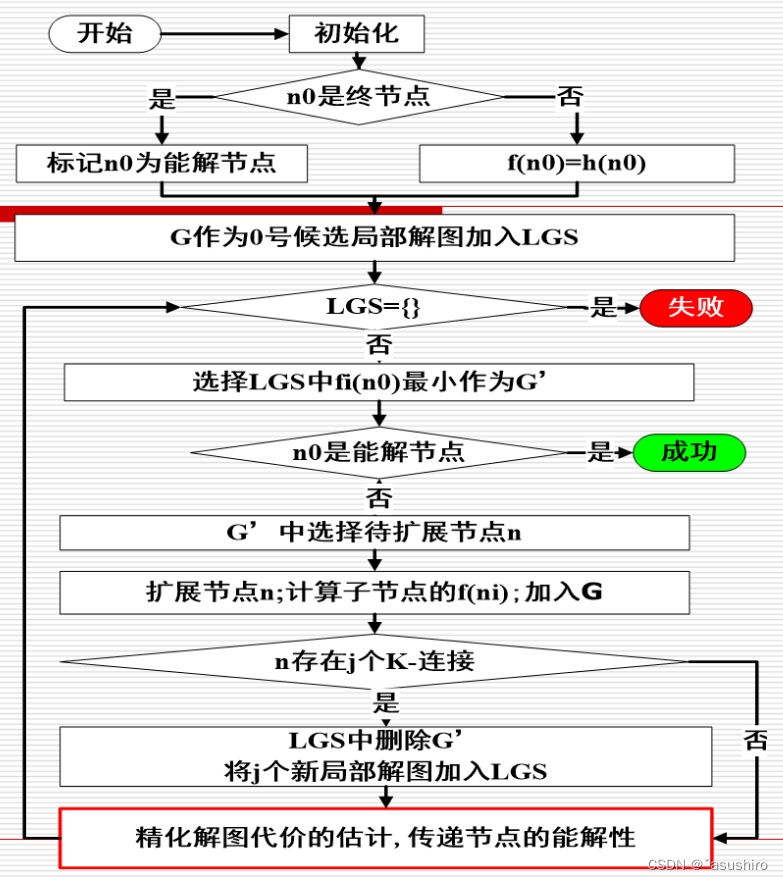
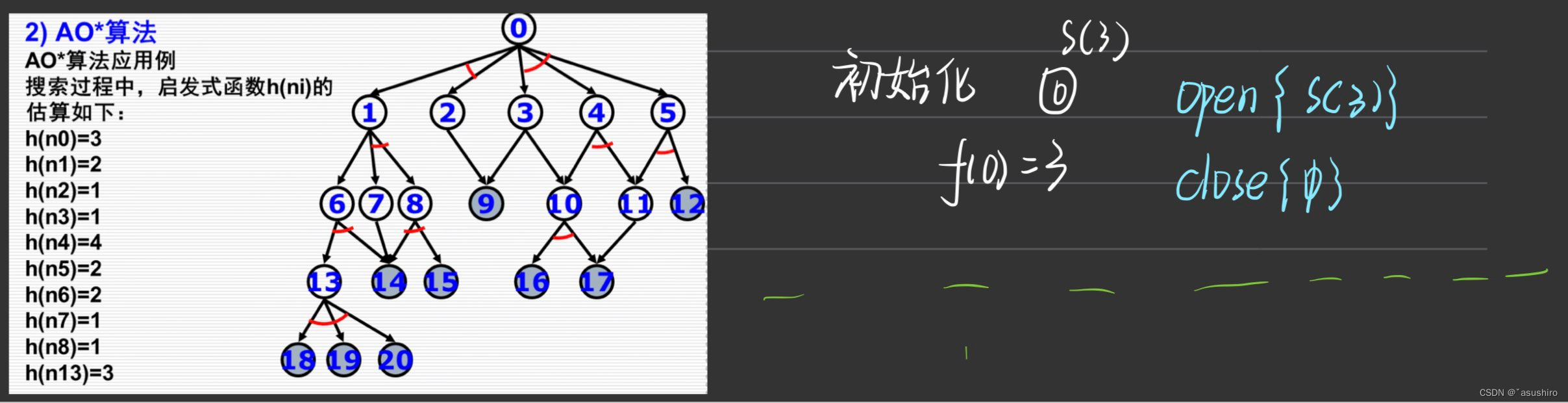
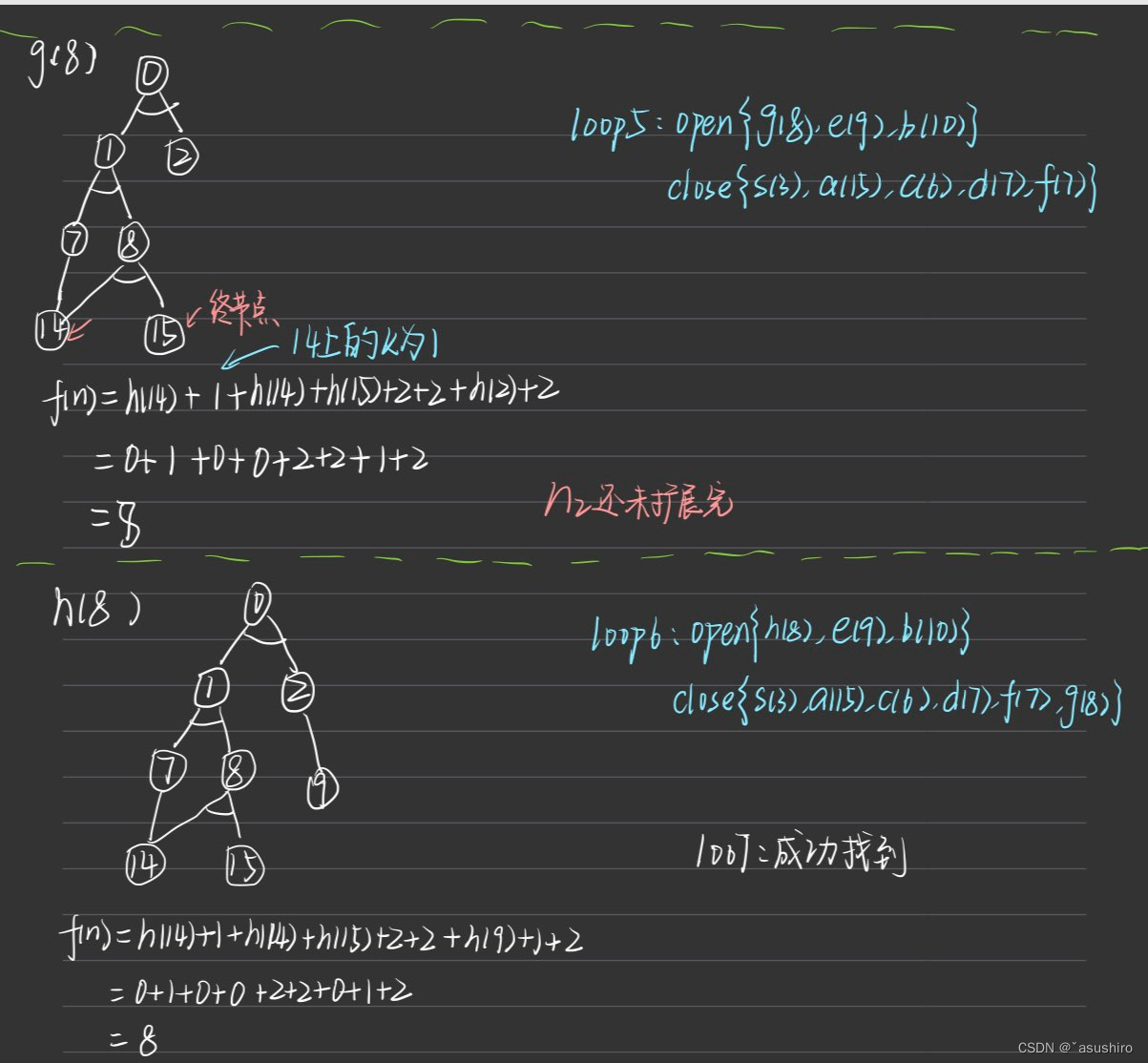
博弈

博弈樹的特點：

• 博弈的初始狀態是初始節點
• 博弈樹的“與”節點和“或”節點是逐層交替出現的
• 整個博弈過程始終站在某一方的立場，讓自己獲勝的為可解節點，讓對方獲勝的都是不可解節點

極大極小過程
考慮對弈若干不之后從可能的走法中選一步相對好的走法來走，即在有限的搜索深度范圍內進行求解。
需要定義一個靜態評估函數f，對棋取臺式進行分析。
雙方定義：
MAX方：有利于，f( p)取正值
MIN方：有利于，f( p)取負值
均衡時f§為0，p代表棋局。

基本思想：

1. 當輪到MIN走步的節點時(取與時），MAX應考慮最壞情況($f(p)$取極小值）
2. 當輪到MAX走步的節點時（取或時），MAX應考慮最好的情況（$f(p)$取極大值）
3. 評價使用1、 2的極值進行推出評估函數的值

過程：
定義博弈樹的層數（往后考慮幾步），設定靜態評估函數（找到最優步），形成博弈樹

優點：

1. 確保最優解: 極大極小過程的一個主要優勢是能夠確保在有限的博弈情境中找到最優解，即使是在較為復雜的游戲中也能找到最優解決方案。
2. 理論上的保證: 在完全信息和有限博弈的情況下，這個算法可以保證找到一個最優解，這是一種理論上的保證。
3. 廣泛適用性: 這種算法不僅限于特定類型的游戲或情景，可以應用于各種類型的博弈，從棋類游戲到經濟決策等。

缺點：

1. 計算復雜度高: 在某些情況下，特別是在博弈樹非常龐大的情況下，極大極小過程需要大量的計算資源和時間，可能會變得不切實際,效率較低。
2. 只適用于完全信息博弈: 這個算法假設所有的信息都是完全可見的，而在現實生活中很多情況下信息并不完整，這限制了它在實際應用中的適用性。

$\alpha ?\beta$過程

---

由于極大極小過程生成博弈樹會生成規定深度的所有節點后在進行評估函數的倒推計算，這使得生成博弈樹和估計值的倒推兩個過程完全分離，因此搜索效率較低。

如果能邊生成博弈樹，邊進行估值計算，則可能不必生成規定深度內的所有節點，以減少搜索的次數，這就是$\alpha ?\beta$過程。

---

好處：$\alpha ?\beta$過程是吧生成后繼節點和倒推評估函數的過程結合起來，及時減掉無用分支來提高算法效率，所以也稱$\alpha ?\beta$剪枝

取MAX節點的最大下界為$\alpha$值
而MIN節點的最小上界為$\beta$值

步驟：

1. 初始化$\beta$為$+\infty$, $\alpha$為$?\infty$
2. 從上至下MAX,MIN交替
3. MAX層只改變$\alpha$
4. MIN層只改變$\beta$
5. $\alpha ,\beta$是傳遞的
6. 當$\alpha >=\beta$時剪枝

下一篇

未完待續