移相干涉技術1-多種干涉條紋仿真模擬生成（原理轉載+代碼實現 包括模擬生成干涉條紋圖）

過去的干涉測量技術是通過人的肉眼或者相機拍攝，來直觀判斷干涉圖中條紋特征進而完成測量，該方法的不穩定因素（比如人的主觀意志）很多，其精度誤差在/10左右38]；現代干涉測量技術通過將電子技術、計算機技術、光電圖像處理技術、算法模型和高精度光學元件結合，大大推動了干涉測量領域的發展，使其進入高精度時代。移相干涉技術(P$)作為現代干涉測量技術的代表，已經成為干涉測量領域學者的研究重點。移相干涉技術測量的原理：移相式激光干涉儀通過控制壓電陶瓷驅動器(PZT)移動參考鏡位置或者改變激光器波長的方式，令參考光和測試光的光程差改變，從干涉圖像中可看出干涉條紋進行了相應的位移。在移相過程中，通過光電探測器(CCD或者CMOS)采集不同移相量下的干涉圖，圖2-1所示為一組移相間隔為90°的移相干涉圖組。計算機根據特定的數學算法和模型對干涉圖組的像素數據進行系列運算，進而可以求得被測元件的面形信息，并根據計算好的相關參數進行質量評價[39（本文移相干涉系統通過驅動PZT模塊完成移相，因此不對基于改變激光器波長以完成移相原理的波長調諧移相技術作介紹)

基于PZT實現移相的過程為：當PZT控制模塊發出指定命令時，PZT伸長量進行相應改變，即參考鏡和被測鏡的相對距離改變，進而完成相位調制以達到移相目的。在上述移相干涉測量過程中，干涉圖像中的條紋分布是由參考光束和測試光束疊加形成的干涉場導致，干涉場的光強信息與干涉圖中像素點的灰度信息相關，其分布函數可表示為：

其中：A(X,y)是干涉圖的背景光強，B(x,y)是調制度，p(X,y)是待測物的波面初始相位信息，6：是移相量，(x,y)是干涉圖中像素點的坐標信息。參考鏡和被測鏡間的面形差P(X,y)與位相分布的關系可表示為：?

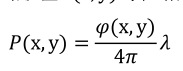
?λ為激光器波長（本文系統為He-Ne激光器一一632.8nm),在移相干涉測量技術中，測量單位為入。當通過解相算法處理干涉圖組的像素數據I:(X,y),可計算出p(x,y),并進一步得到面形信息P(x,y)以完成檢測工作。下面簡單介紹三種本文所設計系統應用到的解相算法（兩種傳統解相算法+一種新穎的平均算法)：

下面是模擬生成干涉條紋圖的代碼

%zernike
clear;clc;close all;[x,y]=meshgrid(-1:0.01:1);k=36;%多項式項數Z=cell(1,36);Z{1,1}=x;Z{1,2}=y;Z{1,3}=-1+2*(x.^2+y.^2);Z{1,4}=x.^2-y.^2;Z{1,5}=2*x.*y;Z{1,6}=-2*y+3*x.*(x.^2+y.^2);Z{1,7}=-2*y+3*y.*(x.^2+y.^2);Z{1,8}=1-6*(x.^2+y.^2)+6*(x.^2+y.^2).^2;Z{1,9}=x.^3-3*x.*y.^2;Z{1,10}=3*x.^2.*y-y.^3;Z{1,11}=-3*x.^2+3*y.^2+4*x.^4-4*y.^4;Z{1,12}=-6*x.*y+8*x.*y*(x.^2+y.^2);Z{1,13}=(10*(x.^2+y.^2).^2-12*(x.^2+y.^2)+3).*x;Z{1,14}=(10*(x.^2+y.^2).^2-12*(x.^2+y.^2)+3).*y;Z{1,15}=20*(x.^2+y.^2).^3-30*(x.^2+y.^2).^2+12*(x.^2+y.^2)-1;Z{1,16}=x.^4-6*x.^2.*y.^2+y.^4;Z{1,17}=4*x.^3.*y-4*x.*y.^3;Z{1,18}=15*(x.^2+y.^2).^2.*x+20*(x.^2+y.^2).*x.^3+12*(x.^2+y.^2).*x-16*x.^3;Z{1,19}=(5*(x.^2+y.^2)-4).*(3*x.^2.*y-y.^3);Z{1,20}=(15*(x.^2+y.^2).^2-20*(x.^2+y.^2)+6).*(x.^2-y.^2);Z{1,21}=(15*(x.^2+y.^2).^2-20*(x.^2+y.^2)+6).*(2*x.*y);Z{1,22}=(35*(x.^2+y.^2).^3-60*(x.^2+y.^2).^2+30*(x.^2+y.^2)-4).*x;Z{1,23}=(35*(x.^2+y.^2).^3-60*(x.^2+y.^2).^2+30*(x.^2+y.^2)-4).*y;Z{1,24}=70*(x.^2+y.^2).^4-140*(x.^2+y.^2).^3+90*(x.^2+y.^2).^2-20*(x.^2+y.^2)+1;Z{1,25}=5*x*(x.^2+y.^2).^2-20*x.^3.*(x.^2+y.^2)+16*x.^5;Z{1,26}=-6*(x.^2+y.^2).*x.^2.*y+14*x.^4.*y-3*x.^2.*y.*(x.^2+y.^2)-2*x.^2.*y.^3+(x.^2+y.^2).*y.^3;Z{1,27}=(6*(x.^2+y.^2)-5).*((x.^2+y.^2).^2-8*(x.^2+y.^2).*x.^2+8*x.^4);Z{1,28}=(6*(x.^2+y.^2)-5).*(4*x.^3.*y-4*x.*y.^3);Z{1,29}=(21*(x.^2+y.^2).^2-30.*(x.^2+y.^2)+10).*(-3*x*(x.^2+y.^2)+4*x.^3);Z{1,30}=(21*(x.^2+y.^2).^2-30.*(x.^2+y.^2)+10).*(3*x.^2.*y-y.^3);Z{1,31}=(56*(x.^2+y.^2).^3-105*(x.^2+y.^2).^2+60*(x.^2+y.^2)-10).*(x.^2-y.^2);Z{1,32}=(56*(x.^2+y.^2).^3-105*(x.^2+y.^2).^2+60*(x.^2+y.^2)-10).*(2*x.*y);Z{1,33}=(126*(x.^2+y.^2).^4-280*(x.^2+y.^2).^3+210*(x.^2+y.^2).^2-60*(x.^2+y.^2)+5).*x;Z{1,34}=(126*(x.^2+y.^2).^4-280*(x.^2+y.^2).^3+210*(x.^2+y.^2).^2-60*(x.^2+y.^2)+5).*y;Z{1,35}=252*(x.^2+y.^2).^5-630*(x.^2+y.^2).^4+560*(x.^2+y.^2).^3-210*(x.^2+y.^2).^2+30*(x.^2+y.^2)-1;Z{1,36}=924*(x.^2+y.^2).^6-2772*(x.^2+y.^2).^5+3150*(x.^2+y.^2).^4-1680*(x.^2+y.^2).^3+420*(x.^2+y.^2).^2-42*(x.^2+y.^2)+1;%單位圓內mask=double((x.^2+y.^2)<=1);for i=1:kZ{1,i}=Z{1,i}.*mask;end%顯示澤爾尼克系數for i=1:ksubplot(6,6,i),imshow(Z{1,i},[]);end%a+(b-a)rand(m,n) ,[a,b]區間m，n維隨機數生成%計算相位P(x,y)，ai根據論文取隨機數% 輸出num=100;%輸出數量for n=1:numfor i=1:k %ai是澤爾尼克基函數的系數，根據論文給出的范圍來定if i==1 %a1=0,P0=0 P=0;endif i==2||i==3 %ai 0,5P=5*rand(1)*Z{1,i}+P;endif i==4 %ai -5,5P=-5+10*rand(1)*Z{1,i}+P;endif i>=5&&i<=9 %ai -0.3,0.3P=-0.2+0.6*rand(1)*Z{1,i}+P;endif i>=10&&i<=36 %ai -0.03,0.03P=-0.03+0.006*rand(1)*Z{1,i}+P;endendP=pi*P.*mask;w=0.2+0.8*rand(1);%w是0.2,1上的隨機數A0min=0.5/(1+w+2*sqrt(w));%A0范圍下限A0max=0.95/(1+w+2*sqrt(w));%A0范圍上限A0=A0min+(A0max-A0min)*rand(1);%生成振幅強度A0x0=-0.2+0.4*rand(201,201);y0=-0.2+0.4*rand(201,201);%x0,y0表示光點在x和y方向上的偏移，這兩個方向都是在[0.2,0.2]范圍內隨機生成的derta=0.9+0.2*rand(1);%光束寬度0.9,1.1%激光源參考光強度Ir=A0*exp(-(((x-x0).^2+(y-y0).^2)/derta^2));%越靠中間(x-x0).^2+(y-y0).^2)越小，越亮% c=cos(P);%cos相位A=(w+1)*Ir;%背景光強B=2*sqrt(w)*Ir;%調制光強I=A+B.*cos(P);%條紋圖I=I.*mask;name=num2str(n);I=imresize(I,[256,256]);imwrite(I,['E:\my_self_progect\matlab\fringes\',name,'.jpg']);endfigure(5),imshow(A,[]);figure(6),imshow(B,[]);figure(7),imshow(A+B.*cos(P),[]);

這段Matlab代碼是一個生成干涉圖像的腳本，其中使用了澤尼克多項式（Zernike polynomials）來模擬光波的相位分布。澤尼克多項式是一組定義在單位圓盤上的正交多項式，它們在光學領域被用于表示波前的相位誤差。這段代碼包含以下幾個主要部分：

  1. 澤尼克多項式的定義：

    • 腳本首先創建了一個坐標網格(x, y)，這個網格覆蓋了[-1, 1]的范圍，步長為0.01。
    • 接下來，定義了36個澤尼克多項式，每個多項式都是x和y的函數，表示不同的波前誤差模式。

  2. 單位圓內的應用：

    • 使用邏輯索引創建了一個掩膜mask，它定義了單位圓內的區域。這意味著多項式只在這個圓內部被考慮。
    • 所有的澤尼克多項式都與這個掩膜相乘，從而確保它們只在單位圓內非零。

  3. 相位計算：

    • 代碼計算了一個相位圖P，這是通過為每個澤尼克多項式隨機分配系數并將它們相加來實現的。
    • 這些系數ai從不同的范圍內隨機選取，這些范圍在注釋中有說明，例如a1=0，ai對于第2和第3項是0到5之間的隨機數，等等。

  4. 干涉圖像生成：

    • 生成了一個強度分布Ir，模擬了一個高斯分布的激光光束。
    • 振幅A模擬了背景光強度，而B模擬了調制光強度。
    • 最后，生成的干涉圖像I由背景光強度和調制光強度的余弦調制組成，余弦項包含了上面計算的相位圖P。

  5. 圖像保存：

    • 腳本將生成的干涉圖像保存到指定的文件夾中。保存的圖像數量由num變量確定。

  6. 顯示圖像：

    • 最后，腳本顯示了背景光強度A，調制光強度B，以及最終的干涉圖像I。

% 清除環境并關閉所有圖像
clear;
clc;
close all;% 定義x和y的網格
[x, y] = meshgrid(linspace(-1, 1, 256), linspace(-1, 1, 256));
mask = double(x.^2 + y.^2 <= 1); % 單位圓的掩膜% 定義澤尼克多項式的系數
% 這里為了簡化，我們只使用前9個澤尼克多項式
coeffs = rand(1, 9) - 0.5; % 隨機生成系數，范圍在[-0.5, 0.5]% 計算澤尼克多項式的線性組合
P = zeros(size(x));
for i = 1:length(coeffs)Z = zernike_polynomial(i, x, y); % 計算第i個澤尼克多項式P = P + coeffs(i) * Z; % 將澤尼克多項式加權后累加
end
P = P .* mask; % 應用掩膜% 設置保存圖像的文件夾
outputFolder = 'E:\gansheyi\matlab\output\folder'; % 更改為您的輸出文件夾路徑
if ~exist(outputFolder, 'dir')mkdir(outputFolder); % 如果輸出文件夾不存在，則創建它
end% 生成和保存9張相移干涉圖像
for n = 1:9phase_shift = (n - 1) * pi / 2; % 相位移動I = 0.5 + 0.5 * cos(P + phase_shift); % 生成干涉圖像I = I .* mask; % 再次應用掩膜% 保存圖像filename = fullfile(outputFolder, sprintf('interference_%d.bmp', n));imwrite(I, filename);% 顯示圖像subplot(3, 3, n);imshow(I, []);title(sprintf('Interference Pattern %d', n));
endfunction Z = zernike_polynomial(n, x, y)% 這個函數根據索引n返回對應的澤尼克多項式r = sqrt(x.^2 + y.^2);theta = atan2(y, x);% 添加更多的澤尼克多項式，如果需要的話switch ncase 1Z = 1;case 2Z = 2 * r .* cos(theta);case 3Z = 2 * r .* sin(theta);% 添加更多的澤尼克多項式，如果需要的話% ...otherwiseZ = 0;end
endUser

?

?增加條紋數

% 初始化環境
clear;
clc;
close all;% 定義x和y的網格
[x, y] = meshgrid(-1:0.01:1);% 定義澤尼克多項式k=36;%多項式項數Z=cell(1,36);Z{1,1}=x;Z{1,2}=y;Z{1,3}=-1+2*(x.^2+y.^2);Z{1,4}=x.^2-y.^2;Z{1,5}=2*x.*y;Z{1,6}=-2*y+3*x.*(x.^2+y.^2);Z{1,7}=-2*y+3*y.*(x.^2+y.^2);Z{1,8}=1-6*(x.^2+y.^2)+6*(x.^2+y.^2).^2;Z{1,9}=x.^3-3*x.*y.^2;Z{1,10}=3*x.^2.*y-y.^3;Z{1,11}=-3*x.^2+3*y.^2+4*x.^4-4*y.^4;Z{1,12}=-6*x.*y+8*x.*y*(x.^2+y.^2);Z{1,13}=(10*(x.^2+y.^2).^2-12*(x.^2+y.^2)+3).*x;Z{1,14}=(10*(x.^2+y.^2).^2-12*(x.^2+y.^2)+3).*y;Z{1,15}=20*(x.^2+y.^2).^3-30*(x.^2+y.^2).^2+12*(x.^2+y.^2)-1;Z{1,16}=x.^4-6*x.^2.*y.^2+y.^4;Z{1,17}=4*x.^3.*y-4*x.*y.^3;Z{1,18}=15*(x.^2+y.^2).^2.*x+20*(x.^2+y.^2).*x.^3+12*(x.^2+y.^2).*x-16*x.^3;Z{1,19}=(5*(x.^2+y.^2)-4).*(3*x.^2.*y-y.^3);Z{1,20}=(15*(x.^2+y.^2).^2-20*(x.^2+y.^2)+6).*(x.^2-y.^2);Z{1,21}=(15*(x.^2+y.^2).^2-20*(x.^2+y.^2)+6).*(2*x.*y);Z{1,22}=(35*(x.^2+y.^2).^3-60*(x.^2+y.^2).^2+30*(x.^2+y.^2)-4).*x;Z{1,23}=(35*(x.^2+y.^2).^3-60*(x.^2+y.^2).^2+30*(x.^2+y.^2)-4).*y;Z{1,24}=70*(x.^2+y.^2).^4-140*(x.^2+y.^2).^3+90*(x.^2+y.^2).^2-20*(x.^2+y.^2)+1;Z{1,25}=5*x*(x.^2+y.^2).^2-20*x.^3.*(x.^2+y.^2)+16*x.^5;Z{1,26}=-6*(x.^2+y.^2).*x.^2.*y+14*x.^4.*y-3*x.^2.*y.*(x.^2+y.^2)-2*x.^2.*y.^3+(x.^2+y.^2).*y.^3;Z{1,27}=(6*(x.^2+y.^2)-5).*((x.^2+y.^2).^2-8*(x.^2+y.^2).*x.^2+8*x.^4);Z{1,28}=(6*(x.^2+y.^2)-5).*(4*x.^3.*y-4*x.*y.^3);Z{1,29}=(21*(x.^2+y.^2).^2-30.*(x.^2+y.^2)+10).*(-3*x*(x.^2+y.^2)+4*x.^3);Z{1,30}=(21*(x.^2+y.^2).^2-30.*(x.^2+y.^2)+10).*(3*x.^2.*y-y.^3);Z{1,31}=(56*(x.^2+y.^2).^3-105*(x.^2+y.^2).^2+60*(x.^2+y.^2)-10).*(x.^2-y.^2);Z{1,32}=(56*(x.^2+y.^2).^3-105*(x.^2+y.^2).^2+60*(x.^2+y.^2)-10).*(2*x.*y);Z{1,33}=(126*(x.^2+y.^2).^4-280*(x.^2+y.^2).^3+210*(x.^2+y.^2).^2-60*(x.^2+y.^2)+5).*x;Z{1,34}=(126*(x.^2+y.^2).^4-280*(x.^2+y.^2).^3+210*(x.^2+y.^2).^2-60*(x.^2+y.^2)+5).*y;Z{1,35}=252*(x.^2+y.^2).^5-630*(x.^2+y.^2).^4+560*(x.^2+y.^2).^3-210*(x.^2+y.^2).^2+30*(x.^2+y.^2)-1;Z{1,36}=924*(x.^2+y.^2).^6-2772*(x.^2+y.^2).^5+3150*(x.^2+y.^2).^4-1680*(x.^2+y.^2).^3+420*(x.^2+y.^2).^2-42*(x.^2+y.^2)+1;
% 應用單位圓掩膜
mask = double((x.^2 + y.^2) <= 1);% 選擇使用一個徑向對稱的澤尼克多項式生成干涉圖
% 這里我們使用Z{1,4} = x^2 - y^2，并增加其系數以增加條紋數
coeff_Z4 = 50; % 調整這個系數可以增加條紋數
P = coeff_Z4 * Z{1,2}; % 使用增大系數的澤尼克多項式
P = P .* mask; % 應用掩膜% 設置保存圖像的文件夾
outputFolder = 'E:\gansheyi_daima\matlab\path_to_your_output_folder2'; % 更改為您的輸出文件夾路徑
if ~exist(outputFolder, 'dir')mkdir(outputFolder); % 如果輸出文件夾不存在，則創建它
end% 生成和保存9張相移干涉圖像
A = 0.5;  % 設置振幅，增加對比度
for n = 1:9% 相位移動phase_shift = (n - 1) * pi / 2;% 生成干涉圖像，增加對比度I = 0.5 + A * cos(P + phase_shift) / 2;I = I .* mask; % 再次應用掩膜% 保存圖像filename = fullfile(outputFolder, sprintf('interference_%d.bmp', n));imwrite(I, filename);
end

?

?生成斜的條紋

直接生成均勻斜向條紋，這通常不需要復雜的澤尼克多項式，因為它們用于模擬更復雜的波前畸變。然而，如果想要使用澤尼克多項式來調整或添加特定的波前畸變，您可以選擇合適的澤尼克多項式并將其加入到相位P中。

% 初始化環境
clear;
clc;
close all;% 定義x和y的網格
[x, y] = meshgrid(-1:0.01:1);% 應用單位圓掩膜
mask = double((x.^2 + y.^2) <= 1);% 創建斜著的條紋相位變化
P = x + y;
P = P .* mask; % 應用掩膜% 設置保存圖像的文件夾
outputFolder = 'E:\gansheyi_daima\matlab\path_to_your_output_folder2'; % 更改為您的輸出文件夾路徑
if ~exist(outputFolder, 'dir')mkdir(outputFolder); % 如果輸出文件夾不存在，則創建它
end% 生成和保存9張相移干涉圖像
A = 0.5;  % 設置振幅，增加對比度
B = 30;   % 系數，用于調整條紋的間距和數量
for n = 1:9% 相位移動phase_shift = (n - 1) * pi / 2;% 生成干涉圖像，增加對比度I = 0.5 + A * cos(B * P + phase_shift) / 2;I = I .* mask; % 再次應用掩膜% 保存圖像filename = fullfile(outputFolder, sprintf('interference_%d.bmp', n));imwrite(I, filename);
end

?

上面舍去了澤妮克多項式的方法，我們下面加上澤妮克系數多項式來

% 初始化環境
clear;
clc;
close all;% 定義x和y的網格
[x, y] = meshgrid(-1:0.01:1);% 定義澤尼克多項式k=36;%多項式項數Z=cell(1,36);Z{1,1}=x;Z{1,2}=y;Z{1,3}=-1+2*(x.^2+y.^2);Z{1,4}=x.^2-y.^2;Z{1,5}=2*x.*y;Z{1,6}=-2*y+3*x.*(x.^2+y.^2);Z{1,7}=-2*y+3*y.*(x.^2+y.^2);Z{1,8}=1-6*(x.^2+y.^2)+6*(x.^2+y.^2).^2;Z{1,9}=x.^3-3*x.*y.^2;Z{1,10}=3*x.^2.*y-y.^3;Z{1,11}=-3*x.^2+3*y.^2+4*x.^4-4*y.^4;Z{1,12}=-6*x.*y+8*x.*y*(x.^2+y.^2);Z{1,13}=(10*(x.^2+y.^2).^2-12*(x.^2+y.^2)+3).*x;Z{1,14}=(10*(x.^2+y.^2).^2-12*(x.^2+y.^2)+3).*y;Z{1,15}=20*(x.^2+y.^2).^3-30*(x.^2+y.^2).^2+12*(x.^2+y.^2)-1;Z{1,16}=x.^4-6*x.^2.*y.^2+y.^4;Z{1,17}=4*x.^3.*y-4*x.*y.^3;Z{1,18}=15*(x.^2+y.^2).^2.*x+20*(x.^2+y.^2).*x.^3+12*(x.^2+y.^2).*x-16*x.^3;Z{1,19}=(5*(x.^2+y.^2)-4).*(3*x.^2.*y-y.^3);Z{1,20}=(15*(x.^2+y.^2).^2-20*(x.^2+y.^2)+6).*(x.^2-y.^2);Z{1,21}=(15*(x.^2+y.^2).^2-20*(x.^2+y.^2)+6).*(2*x.*y);Z{1,22}=(35*(x.^2+y.^2).^3-60*(x.^2+y.^2).^2+30*(x.^2+y.^2)-4).*x;Z{1,23}=(35*(x.^2+y.^2).^3-60*(x.^2+y.^2).^2+30*(x.^2+y.^2)-4).*y;Z{1,24}=70*(x.^2+y.^2).^4-140*(x.^2+y.^2).^3+90*(x.^2+y.^2).^2-20*(x.^2+y.^2)+1;Z{1,25}=5*x*(x.^2+y.^2).^2-20*x.^3.*(x.^2+y.^2)+16*x.^5;Z{1,26}=-6*(x.^2+y.^2).*x.^2.*y+14*x.^4.*y-3*x.^2.*y.*(x.^2+y.^2)-2*x.^2.*y.^3+(x.^2+y.^2).*y.^3;Z{1,27}=(6*(x.^2+y.^2)-5).*((x.^2+y.^2).^2-8*(x.^2+y.^2).*x.^2+8*x.^4);Z{1,28}=(6*(x.^2+y.^2)-5).*(4*x.^3.*y-4*x.*y.^3);Z{1,29}=(21*(x.^2+y.^2).^2-30.*(x.^2+y.^2)+10).*(-3*x*(x.^2+y.^2)+4*x.^3);Z{1,30}=(21*(x.^2+y.^2).^2-30.*(x.^2+y.^2)+10).*(3*x.^2.*y-y.^3);Z{1,31}=(56*(x.^2+y.^2).^3-105*(x.^2+y.^2).^2+60*(x.^2+y.^2)-10).*(x.^2-y.^2);Z{1,32}=(56*(x.^2+y.^2).^3-105*(x.^2+y.^2).^2+60*(x.^2+y.^2)-10).*(2*x.*y);Z{1,33}=(126*(x.^2+y.^2).^4-280*(x.^2+y.^2).^3+210*(x.^2+y.^2).^2-60*(x.^2+y.^2)+5).*x;Z{1,34}=(126*(x.^2+y.^2).^4-280*(x.^2+y.^2).^3+210*(x.^2+y.^2).^2-60*(x.^2+y.^2)+5).*y;Z{1,35}=252*(x.^2+y.^2).^5-630*(x.^2+y.^2).^4+560*(x.^2+y.^2).^3-210*(x.^2+y.^2).^2+30*(x.^2+y.^2)-1;Z{1,36}=924*(x.^2+y.^2).^6-2772*(x.^2+y.^2).^5+3150*(x.^2+y.^2).^4-1680*(x.^2+y.^2).^3+420*(x.^2+y.^2).^2-42*(x.^2+y.^2)+1;
% 應用單位圓掩膜
mask = double((x.^2 + y.^2) <= 1);% 選擇使用一些澤尼克多項式來調整條紋
Zernike_indices = [2, 3]; % 選擇要使用的澤尼克多項式的索引
Zernike_coefficients = [0.5, 0.1]; % 設置選定澤尼克多項式的系數% 創建斜著的條紋相位變化并添加澤尼克畸變
B = 50; % 系數，用于調整條紋的間距和數量
P = B * (x + y); % 基礎斜向條紋
for i = 1:length(Zernike_indices)P = P + Zernike_coefficients(i) * Z{Zernike_indices(i)};
end
P = P .* mask; % 應用掩膜% 設置保存圖像的文件夾
outputFolder = 'E:\gansheyi_daima\matlab\path_to_your_output_folder2'; % 確保這是正確的路徑
if ~exist(outputFolder, 'dir')mkdir(outputFolder); % 如果輸出文件夾不存在，則創建它
end% 生成和保存9張相移干涉圖像
A = 0.5; % 設置振幅，增加對比度
for n = 1:9% 相位移動phase_shift = (n - 1) * pi / 2;% 生成干涉圖像，增加對比度I = 0.5 + A * cos(P + phase_shift);I = I .* mask; % 再次應用掩膜% 保存圖像filename = fullfile(outputFolder, sprintf('interference_%d.bmp', n));imwrite(I, filename);
end

?

整體來說，這段代碼通過模擬光波的相位分布并將其應用于高斯光束，來生成具有波前誤差的干涉圖像。這種方法可以用于模擬實際的光學系統中的波前，并為光學測試和分析提供理論模型。

下面 是讀取9幀移相干涉條紋圖

import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import matplotlib.patches as mpatches# 設置中文兼容字體
plt.rcParams['font.sans-serif'] = ['SimHei']# 創建一個3x3網格的子圖
fig, axs = plt.subplots(3, 3, figsize=(10, 8))# 圖像文件路徑
image_files = [f'C:/Users/Administrator/Desktop/Untitled Folder/matlab/simulation/{i}.bmp' for i in range(9)]# 為每張圖像添加標題和圖例
for ax, image_file, i in zip(axs.ravel(), image_files, range(1, 10)):img = mpimg.imread(image_file)ax.imshow(img, cmap='gray')ax.axis('off')# 設置標題ax.set_title(f'圖{i}')# 創建代理藝術家用于圖例proxy = mpatches.Rectangle((0, 0), 1, 1, fc="w", transform=ax.transAxes, alpha=0)ax.legend([proxy], [f'圖例{i}'], loc='upper right')plt.tight_layout()
plt.show()

matlab 的代碼：

% 設置圖像文件夾和文件名
folder = 'C:/Users/Administrator/Desktop/Untitled Folder/matlab/simulation/'; % 更改為您的圖像文件夾路徑
filePattern = fullfile(folder, '*.bmp');
bmpFiles = dir(filePattern);% 創建一個新圖形窗口
figure;% 遍歷所有圖像文件
for k = 1:9baseFileName = bmpFiles(k).name;fullFileName = fullfile(folder, baseFileName);fprintf(1, 'Now reading %s\n', fullFileName);% 讀取圖像imageArray = imread(fullFileName);imageSize = size(imageArray);% 創建掩膜（圓形）[columnsInImage, rowsInImage] = meshgrid(1:imageSize(2), 1:imageSize(1));% 中心點centerX = imageSize(2) / 2;centerY = imageSize(1) / 2;% 半徑radius = min([centerX centerY]) - 5; % 減5像素以保持圓形在圖像內部% 創建二維邏輯索引circlePixels = (rowsInImage - centerY).^2 ...+ (columnsInImage - centerX).^2 <= radius.^2;% 初始化一個全黑的圖像maskedImage = uint8(zeros(size(imageArray)));% 使用圓形掩膜來定義ROI區域內的像素maskedImage(circlePixels) = imageArray(circlePixels);% 顯示圖像subplot(3,3,k);imshow(maskedImage); % 顯示應用掩膜后的圖像title(sprintf('Image #%d', k));
end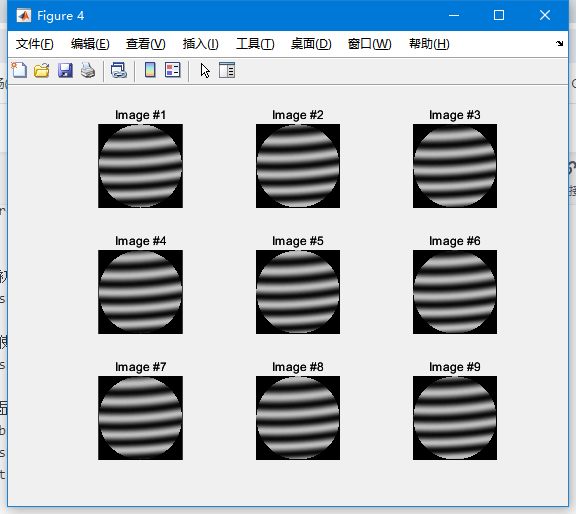

四步移相法：

作為經典的解相算法，四步移相法4]可以有效計算出理想移相圖組的相位分布。先獲取無移相的干涉圖像，再進行三次移相間隔為π/2的移相，每次移相完成采集1幀圖像，共得到4幀相位相差π/2的干涉圖像，其圖像光強信息分別為：

?(2.3)~(2.6)進行公式變換消去A和B可得到p(x,y)和四幀圖像像素信息的關系式：

?該算法求解速度快，適合對理想干涉圖組進行求解。當有外部干擾時，相位變化呈無規則態，此時四步移相法的解相效果非常糟糕，無任何抗振能力。與四步移相法類似的單周期定步長算法還有三步算法等。

其中原理部分轉載與下方碩士論文：

參考文獻：翟天保 碩士論文 基于干涉圖像質量分析的激光干涉儀抗振技術研究

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/210338.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/210338.shtml
英文地址，請注明出處：http://en.pswp.cn/news/210338.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

智能優化算法應用：基于廚師算法無線傳感器網絡(WSN)覆蓋優化 - 附代碼

智能優化算法應用：基于廚師算法無線傳感器網絡(WSN)覆蓋優化 - 附代碼

智能優化算法應用&#xff1a;基于廚師算法無線傳感器網絡(WSN)覆蓋優化 - 附代碼 文章目錄 智能優化算法應用&#xff1a;基于廚師算法無線傳感器網絡(WSN)覆蓋優化 - 附代碼1.無線傳感網絡節點模型2.覆蓋數學模型及分析3.廚師算法4.實驗參數設定5.算法結果6.參考文獻7.MATLAB…
閱讀更多...
代碼隨想錄-刷題第二十一天

代碼隨想錄-刷題第二十一天

530.二叉搜索樹的最小絕對差 題目鏈接&#xff1a;530. 二叉搜索樹的最小絕對差 思路&#xff1a;二叉搜索樹的中序遍歷是有序的。根據二叉搜索樹的這個特性來解題。 class Solution {// 同樣利用二叉樹中序遍歷是一個有序數組。private List<Integer> list new Arra…
閱讀更多...
一加 12 Pop-up快閃活動來襲，十城聯動火爆開啟

一加 12 Pop-up快閃活動來襲，十城聯動火爆開啟

12 月 9 日&#xff0c;一加 12 Pop-up 快閃活動在北京、深圳、上海、廣州等十城聯動開啟&#xff0c;各地加油歡聚快閃現場&#xff0c;搶先體驗與購買一加 12。作為一加十年超越之作&#xff0c;一加 12 全球首發擁有醫療級護眼方案和行業第一 4500nit 峰值亮度的 2K 東方屏、…
閱讀更多...
C++新經典模板與泛型編程：策略類模板

C++新經典模板與泛型編程：策略類模板

策略類模板 在前面的博文中&#xff0c;策略類SumPolicy和MinPolicy都是普通的類&#xff0c;其中包含的是一個靜態成員函數模板algorithm()&#xff0c;該函數模板包含兩個類型模板參數。其實&#xff0c;也可以把SumPolicy和MinPolicy類寫成類模板—直接把algorithm()中的兩…
閱讀更多...
【Linux】無法使用 ifconfig 查看系統網絡接口信息，報錯 command not found: ifconfig

【Linux】無法使用 ifconfig 查看系統網絡接口信息，報錯 command not found: ifconfig

問題描述 ifconfig是一個用于配置和顯示系統網絡接口信息的命令行工具。它通常用于Unix、Linux和其他類Unix系統中。 通過ifconfig命令&#xff0c;你可以查看和修改系統中網絡接口的配置信息&#xff0c;包括IP地址、子網掩碼、MAC地址、MTU&#xff08;最大傳輸單元&#x…
閱讀更多...
javacv踩坑記錄

javacv踩坑記錄

前一陣學習opencv&#xff0c;發現在做人臉識別的時候遇到一些類庫不存在的情況&#xff0c;查找后發現是由于拓展包沒有安裝完全&#xff08;僅安裝了基礎版&#xff09;。由于網絡的問題&#xff08;初步猜測&#xff09;&#xff0c;始終無法安裝好拓展包。 于是另辟蹊徑&am…
閱讀更多...
MongoDb數據庫

MongoDb數據庫

一、命令交互 1.1 數據庫命令 1.顯示所有數據庫&#xff1a; show dbs 2.切換到指定數據庫&#xff0c;如果沒有則自動創建數據庫 use databaseName 3.顯示當前所在數據庫 db 4.刪除當前數據庫 use 庫名 db.dropDatabase() 1.2 集合命令 1.創建集合 db.createColl…
閱讀更多...
[文檔級關系抽取｜ACL論文]文檔級關系抽取中語言理解的基礎模型

[文檔級關系抽取｜ACL論文]文檔級關系抽取中語言理解的基礎模型

Did the Models Understand Documents? Benchmarking Models for Language Understanding in Document-Level Relation Extraction School of Computer Science, Fudan University | ACL 2023.06 | 原文鏈接 Background 過去的工作大多數都是從單個句子中收獲更多的關系&am…
閱讀更多...
MongoDB中的$type操作符和limit與skip方法

MongoDB中的$type操作符和limit與skip方法

本文主要介紹MongoDB中的$type操作符和limit與skip方法。 目錄 MongoDB的$type操作符MongoDB的limit方法MongoDB的skip方法 MongoDB的$type操作符 MongoDB中的$type操作符用于檢查一個字段的類型是否與指定的類型相匹配。它可以用于查詢和投影操作。 $type操作符可以與以下數…
閱讀更多...
php,redis實現一個電影熱度排行榜

php,redis實現一個電影熱度排行榜

要實現電影熱度排行榜&#xff0c;需要記錄每個電影的熱度值&#xff0c;熱度值可以根據不同的算法計算&#xff0c;例如&#xff1a;觀看次數、評分數、評論數等。這里我們以觀看次數為例。 首先&#xff0c;需要使用 Redis 的 Sorted Set 數據結構來存儲電影的熱度值和電影 …
閱讀更多...
JVS低代碼表單引擎：數據校驗與處理的先鋒

JVS低代碼表單引擎：數據校驗與處理的先鋒

隨著信息技術的迅速發展&#xff0c;數據校驗與處理已經成為了各類應用中不可或缺的一環。尤其是在涉及敏感信息&#xff0c;如密碼處理時&#xff0c;其安全性和準確性顯得尤為重要。JVS低代碼表單引擎提供了強大的文本組件觸發邏輯校驗功能&#xff0c;它能夠在用戶填寫數據的…
閱讀更多...
截取字符串

截取字符串

輸入一個字符串和一個整數 k &#xff0c;截取字符串的前k個字符并輸出。 數據范圍&#xff1a;字符串長度滿足 1≤n≤1000&#xff0c; 1≤k≤n 輸入描述&#xff1a; 1.輸入待截取的字符串 2.輸入一個正整數k&#xff0c;代表截取的長度 輸出描述&#xff1a;截取后的字符串…
閱讀更多...
模電·放大電路的分析方法——等效電路法

模電·放大電路的分析方法——等效電路法

放大電路的分析方法——等效電路法 晶體管的直流模型及靜態工作點的估算法晶體管共射h參數等效模型 h h h參數等效模型的由來參數的物理意義簡化的h參數等效模型 r b e {r\tiny be} rbe的近似表達式 共射放大電路動態參數的分析電壓放大倍數 A ˙ u \.{A}\tiny u A˙u輸入電阻 …
閱讀更多...
三種配置Spring程序的方法

三種配置Spring程序的方法

1 使用XML文件配置Spring程序 在XML文件中使用bean標簽&#xff0c;將其交給容器管理 class: 指定bean對應的類型的全限定名稱id: 用于指定一個名稱&#xff0c;作為該bean的唯一標識符&#xff0c;如果不需要id&#xff0c;也可不指定該屬性name: 用于指定bean的別名&#x…
閱讀更多...
【小米電腦管家】安裝使用教程--非小米電腦

【小米電腦管家】安裝使用教程--非小米電腦

安裝說明功能體驗下載資源 Xiaomi HyperOS發布后&#xff0c;小米妙享電腦端獨立版本也走向終點&#xff0c;最新的【小米電腦管家】將會內置妙享實現萬物互聯。那么本篇文章將分享非小米電腦用戶如何繞過設備識別驗證安裝使用【小米電腦管家】實現萬物互聯 安裝說明 1.解壓文…
閱讀更多...
如何用Python編寫俄羅斯方塊Tetris游戲？

如何用Python編寫俄羅斯方塊Tetris游戲？

在本文中&#xff0c;我們將用Python代碼構建一個令人驚嘆的項目&#xff1a;俄羅斯方塊游戲。在這個項目中&#xff0c;我們將使用pygame庫來構建游戲。要創建此項目&#xff0c;請確保您的系統中安裝了最新版本的Python。讓我們開始吧&#xff01; Pygame是一組跨平臺的Pyth…
閱讀更多...
wireshark過濾包小技巧

wireshark過濾包小技巧

1、過濾包含某個字符串的數據包&#xff1a; 或者&#xff1a; 2、過濾包含某一連續十六進制的數據包&#xff1a; 或者&#xff1a; 3、過濾精確到位數位置 或者&#xff1a;
閱讀更多...
關于使用EB tresos出現無法激活的情況解決

關于使用EB tresos出現無法激活的情況解決

EB安裝完成時需要激活才能使用的&#xff0c;不然都無法建立工程。 我在安裝eb studio時就是在激活方面有問題導致無法使用&#xff0c;下面講解出現了什么問題以及我如何去解除的。 1.出現的錯誤提示&#xff1f; ERROR&#xff1a;flexActAPPActivationSend按照在官網中&…
閱讀更多...
低代碼：輕松構建應用程序的新時代

低代碼：輕松構建應用程序的新時代

在當今數字化時代&#xff0c;應用程序對于日常企業業務的開展&#xff0c;已經成為一種剛需。然而&#xff0c;應用程序開發的過程往往耗時耗力&#xff0c;對于企業來講&#xff0c;是一筆不小的成本開支。低代碼問世以來&#xff0c;一直在嘗試為業務人員賦能&#xff0c;讓…
閱讀更多...
扁平按鈕樣式

扁平按鈕樣式

上圖 代碼&#xff1a; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>扁平按鈕</title><style>body {margin: 0;padding: 0;height: 100vh;display: flex;justify-content: center;ali…
閱讀更多...
最新文章

Copyright @ 2022~2023